A capacitor of capacitance 4μF is charged to 80V and another capacitor of capacitance 6μF is charged to 30V are connected to each other using zero resistance wires such that the positive plate of one capacitor is connected to the positive plate of the other. The energy lost by the 4μF capacitor in the process in X∗10−4J. Find the value of X.
The correct Answer is:78
To solve the problem, we need to follow these steps:
Step 1: Calculate the initial energy stored in the 4μF capacitor.
The formula for the energy stored in a capacitor is given by:
U=12CV2
For the 4μF capacitor charged to 80V:
U1=12×4×10−6F×(80V)2
Calculating this:
U1=12×4×10−6×6400=12×25600×10−6=12800×10−6J=0.0128J
Step 2: Calculate the initial energy stored in the 6μF capacitor.
For the 6μF capacitor charged to 30V:
U2=12×6×10−6F×(30V)2
Calculating this:
U2=12×6×10−6×900=12×5400×10−6=2700×10−6J=0.0027J
Step 3: Calculate the total charge on both capacitors.
The charge on the 4μF capacitor:
Q1=C1V1=4×10−6F×80V=320×10−6C
The charge on the 6μF capacitor:
Q2=C2V2=6×10−6F×30V=180×10−6C
Total charge when connected in parallel:
Qtotal=Q1+Q2=320×10−6+180×10−6=500×10−6C
Step 4: Calculate the equivalent capacitance.
When connected in parallel, the equivalent capacitance Ceq is:
Ceq=C1+C2=4×10−6+6×10−6=10×10−6F
Step 5: Calculate the common potential across the capacitors.
Using the total charge and equivalent capacitance:
Vcommon=QtotalCeq=500×10−610×10−6=50V
Step 6: Calculate the final energy stored in the 4μF capacitor.
Using the common potential:
U′1=12C1V2common=12×4×10−6×(50)2
Calculating this:
U′1=12×4×10−6×2500=12×10000×10−6=5000×10−6J=0.005J
Step 7: Calculate the energy lost by the 4μF capacitor.
The energy lost is:
ΔU=U1−U′1=0.0128−0.005=0.0078J
Step 8: Convert the energy lost into the required format.
To express this in the form X×10−4J:
0.0078J=78×10−4J
Thus, X=78.
Final Answer:
The value of X is 78.
The formula for the energy stored in a capacitor is given by:
U=12CV2
For the 4μF capacitor charged to 80V:
U1=12×4×10−6F×(80V)2
Calculating this:
U1=12×4×10−6×6400=12×25600×10−6=12800×10−6J=0.0128J
For the 6μF capacitor charged to 30V:
U2=12×6×10−6F×(30V)2
Calculating this:
U2=12×6×10−6×900=12×5400×10−6=2700×10−6J=0.0027J
The charge on the 4μF capacitor:
Q1=C1V1=4×10−6F×80V=320×10−6C
The charge on the 6μF capacitor:
Q2=C2V2=6×10−6F×30V=180×10−6C
Total charge when connected in parallel:
Qtotal=Q1+Q2=320×10−6+180×10−6=500×10−6C
When connected in parallel, the equivalent capacitance Ceq is:
Ceq=C1+C2=4×10−6+6×10−6=10×10−6F
Using the total charge and equivalent capacitance:
Vcommon=QtotalCeq=500×10−610×10−6=50V
Using the common potential:
U′1=12C1V2common=12×4×10−6×(50)2
Calculating this:
U′1=12×4×10−6×2500=12×10000×10−6=5000×10−6J=0.005J
The energy lost is:
ΔU=U1−U′1=0.0128−0.005=0.0078J
To express this in the form X×10−4J:
0.0078J=78×10−4J
Thus, X=78.
The value of X is 78.
Topper's Solved these Questions
Similar Questions
A capacitor of capacitor 5.00μF is charged to24.0V and another capacitor of capacitance 6.0μF is charged to 12.0V (a) Find the energy stored in each capacitor .(b)The positive plates of the first capacitor is now connected to the negative plate of the second and vice versa . Find the new charges on the capacitors .(c)Find the loss of electrostatic energy during the process .(d)Where does this energy go?
View SolutionA capacitor A of capacitance 4μF is charged to 30V and another capacitor B of capacitance 2μF is charged to 15V. Now, the positive plate of A is connected to the negative plate of B and negative plate of A to the positive plate of B. find the final charge of each capacitor and loss of electrostatic energy in the process.
View Solution4μF capacitor is charged to 150 V and another capacitor of 6μF is charged to 200 V. Then they are connected across each other. Find the potential difference across them. Calculate the heat produced.
View Solution4μF capacitor is charged to 150 V and another capacitor of 6μF is charged to 200 V. Then they are connected across each other. Find the potential difference across them. Calculate the heat produced.
View SolutionTwo capacitors of capacitances 3μF and 6μF are charged to a potential of 12V each. They are now connected to each other, with the positive plate of each joined to the negative plate of the other. The potential difference across each will be
View SolutionThe charge on the 4μF capacitor in the steady state is
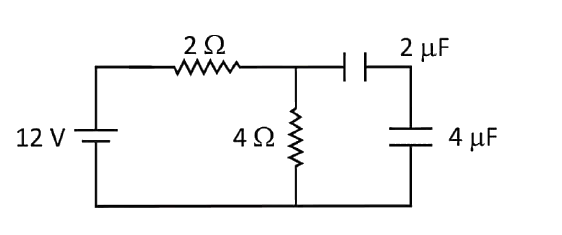
View SolutionThe charge on the capacitor of capacitance 10μF in steady state condition in the circuit shown is
_PHY_E05_271_Q01.png)
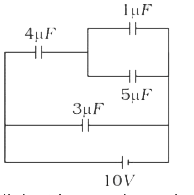
View SolutionThe charge on the 4μF capacitor at steady state is (in μC)
View SolutionA capacitor of capacitance C which is initially charged up to a potential differnce ε is connected with a battery of emf ε2 such that the positive terminal of the battery is connected with the positive plate of the capacitor. Find the heat loss in the circuit the process of charging.
View SolutionTwo capacitors of capacitance 2μF and 3μF respectively are charged to potential difference 20 V and 40 V respectively. Now the capacitors are connected in series with a resistance such that the positively charged plate of one capacitor is connected to the positively charged plate of the other. The initial current through the resistance is I0. The potential difference across the 2μF capacitor at the instant the current has reduced to I02 is_______ V.
View Solution
