In the above problem the angular velocity of the system after the particle sticks to it will be?
0.3 rad/s
5.3 rad/s
10.3 rad/s
89.3 rad/s
To find the angular velocity of the system after a particle sticks to a rotating solid cylinder, we can follow these steps:
Step 1: Identify the given data
- Mass of the solid cylinder (M) = 2 kg
- Radius of the solid cylinder (R) = 0.2 m
- Initial angular velocity of the cylinder (ω_initial) = 3 rad/s
- Mass of the particle (m) = 0.5 kg
- Velocity of the particle (v) = 5 m/s
Step 2: Calculate the moment of inertia of the solid cylinder
The moment of inertia (I) of a solid cylinder about its axis is given by the formula:
I=12MR2
Substituting the values:
I=12×2kg×(0.2m)2
I=12×2×0.04
I=0.04kg m2
Step 3: Calculate the initial angular momentum of the system
The initial angular momentum (L_initial) of the cylinder is given by:
Linitial=I⋅ωinitial
Substituting the values:
Linitial=0.04kg m2⋅3rad/s
Linitial=0.12kg m2/s
The angular momentum of the particle just before it sticks to the cylinder is given by:
Lparticle=m⋅v⋅R
Substituting the values:
Lparticle=0.5kg⋅5m/s⋅0.2m
Lparticle=0.5⋅5⋅0.2=0.5kg m2/s
Step 4: Calculate the total initial angular momentum
The total initial angular momentum (L_total_initial) is the sum of the angular momentum of the cylinder and the particle:
Ltotal initial=Linitial+Lparticle
Ltotal initial=0.12+0.5=0.62kg m2/s
Step 5: Calculate the moment of inertia of the system after the particle sticks
After the particle sticks to the cylinder, the total moment of inertia (I_total) of the system is:
Itotal=I+mR2
Substituting the values:
Itotal=0.04+0.5⋅(0.2)2
Itotal=0.04+0.5⋅0.04
Itotal=0.04+0.02=0.06kg m2
Step 6: Apply conservation of angular momentum
According to the conservation of angular momentum:
Ltotal initial=Ltotal final
Where Ltotal final=Itotal⋅ωfinal.
Setting the equations equal gives:
0.62=0.06⋅ωfinal
Step 7: Solve for the final angular velocity
Rearranging the equation to solve for ωfinal:
ωfinal=0.620.06
ωfinal=10.33rad/s
Final Answer
The angular velocity of the system after the particle sticks to it is approximately 10.33 rad/s.
---
- Mass of the solid cylinder (M) = 2 kg
- Radius of the solid cylinder (R) = 0.2 m
- Initial angular velocity of the cylinder (ω_initial) = 3 rad/s
- Mass of the particle (m) = 0.5 kg
- Velocity of the particle (v) = 5 m/s
The moment of inertia (I) of a solid cylinder about its axis is given by the formula:
I=12MR2
Substituting the values:
I=12×2kg×(0.2m)2
I=12×2×0.04
I=0.04kg m2
The initial angular momentum (L_initial) of the cylinder is given by:
Linitial=I⋅ωinitial
Substituting the values:
Linitial=0.04kg m2⋅3rad/s
Linitial=0.12kg m2/s
Lparticle=m⋅v⋅R
Substituting the values:
Lparticle=0.5kg⋅5m/s⋅0.2m
Lparticle=0.5⋅5⋅0.2=0.5kg m2/s
The total initial angular momentum (L_total_initial) is the sum of the angular momentum of the cylinder and the particle:
Ltotal initial=Linitial+Lparticle
Ltotal initial=0.12+0.5=0.62kg m2/s
After the particle sticks to the cylinder, the total moment of inertia (I_total) of the system is:
Itotal=I+mR2
Substituting the values:
Itotal=0.04+0.5⋅(0.2)2
Itotal=0.04+0.5⋅0.04
Itotal=0.04+0.02=0.06kg m2
According to the conservation of angular momentum:
Ltotal initial=Ltotal final
Where Ltotal final=Itotal⋅ωfinal.
0.62=0.06⋅ωfinal
Rearranging the equation to solve for ωfinal:
ωfinal=0.620.06
ωfinal=10.33rad/s
The angular velocity of the system after the particle sticks to it is approximately 10.33 rad/s.
Topper's Solved these Questions
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE-5
5 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE-6
5 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE-3
5 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - IMPECCABLE
56 Videos
Similar Questions
In the above question, the angular velocity will:
View Solution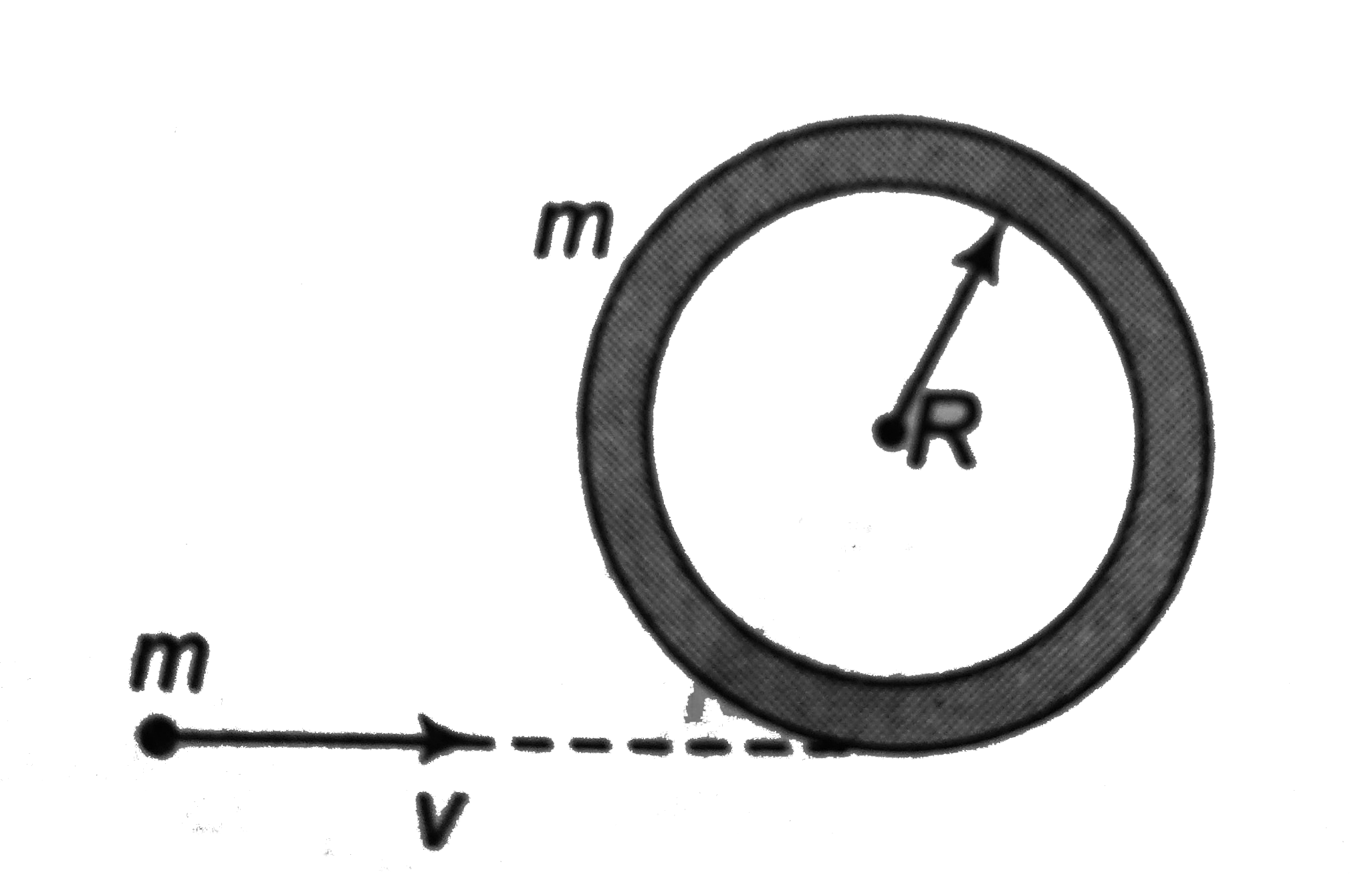
A circular ring of mass m and radius R rests flat on a horizontal smooth surface as shown in figure. A particle of mass m, and moving with a velocity v. Collides inelastically (e=0) with the ring the angular velocity with which the system rotates after the particle strikes the ring is
View SolutionIn the above problem the displacement after 2 s is:
View SolutionIn the above problem, find total mechanical energy of the system .
View SolutionThe angular momentum of a system of particles is conserved
View SolutionIn the above problem the angular velocity of the system after the particle sticks to it will be?
View SolutionWhat is the angular acceleration of a particle if the angular velocity of a particle becomes 4 times of its initial angular velocity 1 rad s in 2 seconds
View SolutionWhat is the angular acceleration of a particle if the angular velocity of a particle becomes 4 times of its initial angular velocity 1 rad s in 2 seconds
View SolutionWhat is the angular velocity of a particle lying on the axis of rotation ?
View SolutionWhat is the angular velocity of a particle lying on the axis of rotation ?
View Solution
