What is the angular velocity of a particle lying on the axis of rotation ?
To solve the question of what the angular velocity of a particle lying on the axis of rotation is, we can follow these steps:
1. Understand the Concept of Angular Velocity:
Angular velocity (ω) is defined as the rate of change of angular displacement with respect to time. It describes how fast an object is rotating around an axis.
2. Identify the Axis of Rotation:
In this scenario, we have a rigid body with a defined axis of rotation. The axis of rotation is the line around which the body rotates.
3. Locate the Particle:
We are considering a particle (let's call it P) that lies directly on the axis of rotation.
4. Analyze the Motion of the Particle:
A particle that is on the axis of rotation does not experience any circular motion. Instead, it remains stationary relative to the axis itself.
5. Determine the Angular Velocity:
Since the particle P does not move in a circular path (as it is on the axis), its angular velocity is effectively zero. Mathematically, we can express this as:
Angular Velocity (ω)=0 (for particle P on the axis of rotation)
6. Conclusion:
Therefore, the angular velocity of a particle lying on the axis of rotation is 0.
Final Answer:
The angular velocity of a particle lying on the axis of rotation is 0.
---
Angular velocity (ω) is defined as the rate of change of angular displacement with respect to time. It describes how fast an object is rotating around an axis.
In this scenario, we have a rigid body with a defined axis of rotation. The axis of rotation is the line around which the body rotates.
We are considering a particle (let's call it P) that lies directly on the axis of rotation.
A particle that is on the axis of rotation does not experience any circular motion. Instead, it remains stationary relative to the axis itself.
Since the particle P does not move in a circular path (as it is on the axis), its angular velocity is effectively zero. Mathematically, we can express this as:
Angular Velocity (ω)=0 (for particle P on the axis of rotation)
Therefore, the angular velocity of a particle lying on the axis of rotation is 0.
The angular velocity of a particle lying on the axis of rotation is 0.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - J) Aakash Challengers Questions
13 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
Similar Questions
What is the angular acceleration of a particle if the angular velocity of a particle becomes 4 times of its initial angular velocity 1 rad s in 2 seconds
View SolutionWhat is the angular acceleration of a particle if the angular velocity of a particle becomes 4 times of its initial angular velocity 1 rad s in 2 seconds
View Solution
Knowledge Check
Assertion: If the head of a right handed screw rotates with the body, the screw advances in the direction of the angular velocty.
Reason: For rotation about a fixed axis, the angular velocity vector lies along the axis of rotation.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertionCIf assertion is true but reason is false.DIf both assertion and reason are false.
What is the angular acceleration of a particle moving with constant angular velocity ?
View SolutionWhat is the angular acceleration of a particle moving with constant angular velocity ?
View SolutionVelocity of particle parallel to y- axis is
View SolutionThe angular velocity of a particle moving in a circle realative to the center of the circle is equal to ω. Find the angular velocity of the particle relative to a point on the circular path.
View SolutionA particle mass parallel to x-axis with constant velocity v as shown in the figure. The angular velocity of the particle about the origin O
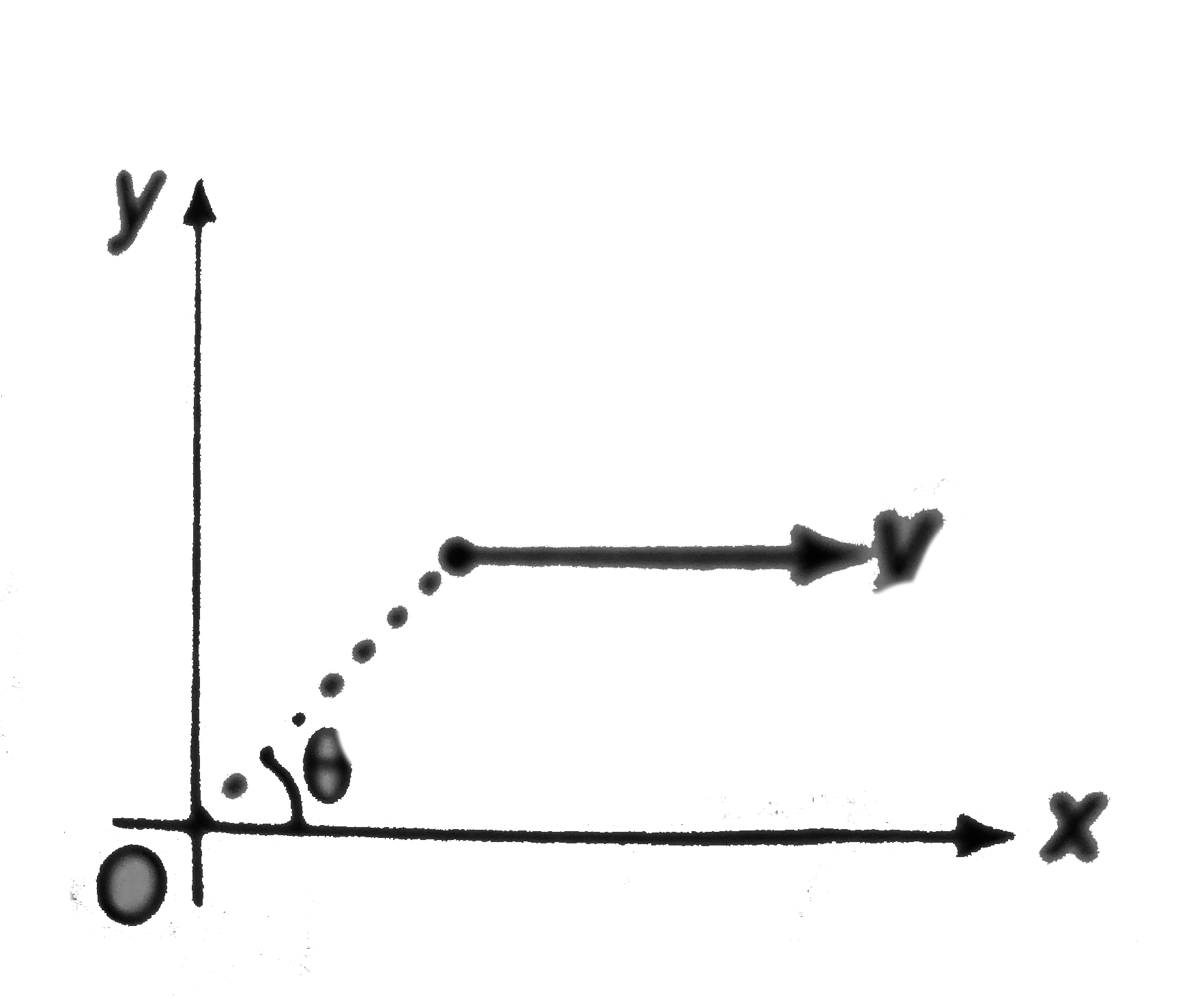
View SolutionA solid cylinder of mass 20kg rotates about its axis with angular velocity of 100 radian s−1. The radius of the cylinder is 0.25m. The magnitude of the angular momentum of the cylinder about its axis of rotation is
View SolutionA particle is moving parallel to x-axis as shown in the figure. The angular velocity of the particle about the origin is
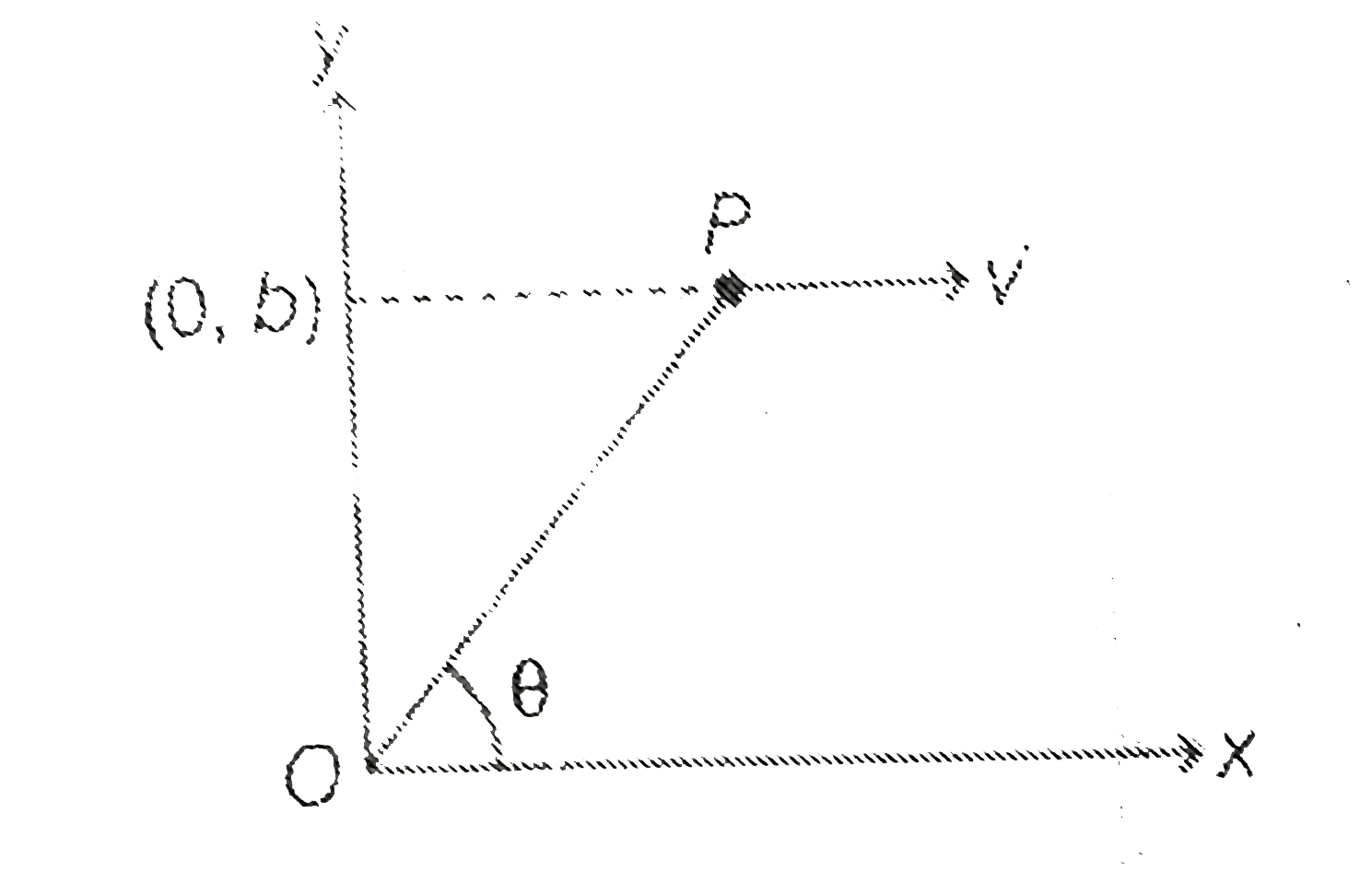
View Solution
