The cue stick hits a cue ball horizontally a distance x above the centre of the ball. Find the value of x for which the cue ball will instantaneously roll without slipping. Calculate the answer in terms of the radius R of the ball.
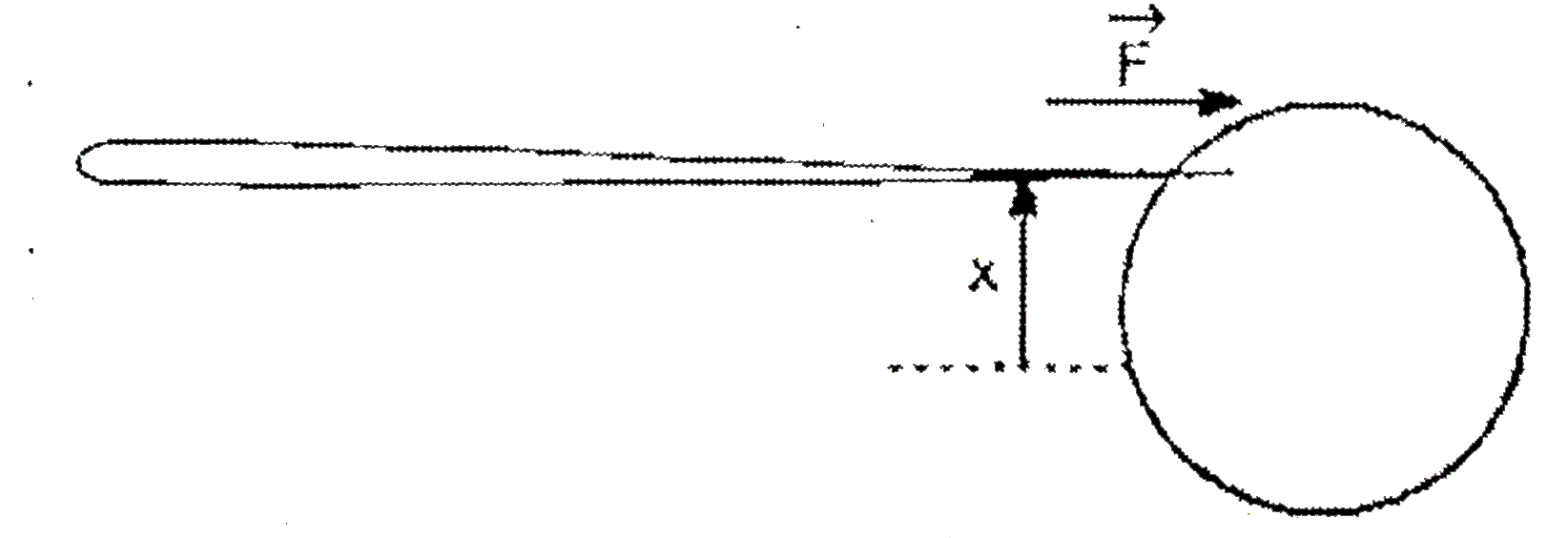
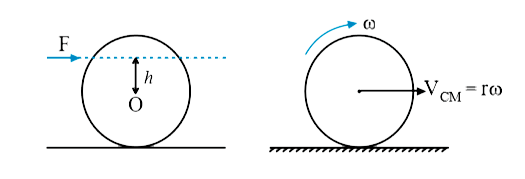
The horizontal force creates a linear impulse and angular impulse.I=∫FdtJ=∫τdt=lhLinear impulse = change in linear momentum ⇒I=MVCm−0..(i) Angular impulse about CM = change in angular momentum J=lh=25mr2ω−0..(ii)Dividing (ii) and(i) we get h=2Mr2ω5MVCM Using VCM=rωh=R5R.
Topper's Solved these Questions
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - SOLVED EXAMPLES
20 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE-1
4 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - IMPECCABLE
56 Videos
Similar Questions

A solid sphere of mass M and radius R is hit by a cue at a height h above the centre C. for what value of h the sphere will rool without slipping ?
View Solution
A billiard ball, initially at rest, is given a sharp impulse by a cue. The cue is held horizontally a distance h above the centre line as shown in figure. The ball leaves the cue with a speed v0 and because of its forward english (backward slipping) eventually acquires a final
speed 97v0 show that h=45R
Where R is the radius of the ball.
View SolutionA ball is projected from ground with a speed 70m/s at an angle 45∘ with the vertical so that it strikes a vertical wall at horizontal distance 4903m from the point of projection. If the ball returns back to the poin tof projection without any collision with ground then find the coefficient of restitution between the ball and wall.
View SolutionA ball is thrown with the velocity u at an angle of α to the horizon. Find (i) the height of which the ball will rise to (ii) the distance x from the point of projection to the point where it reaches to the ground and (iii) the time during which the ball will be in motion (neglect the air resistance ).
View SolutionA uniform sphere of radius R is palced on a rough horizontal surface and given a linear velocity v0 and an angular velocity ω0 as shown . If the angular velocity and the linear velocity both become zero simultaneously, then
View SolutionA ball of mass 0.2 kg rests on a vertical post of height 5 m. A bullet of mass 0.01 kg, travelling with a velocity Vm/s in a horizontal direction, hits the centre of the ball. After the collision, the ball and bullet travel independently. The ball hits the ground at a distance of 20 m and the bullet at a distance of 100 m from the foot of the post. The velocity V of the bullet is

View SolutionTouching a hemispherical dome of radius R there is a vertical tower of height H=4r. A boy projects a ball horizontally at speed u from the top of the tower. The ball strikes the dome at a height R2 from ground and rebounds. After rebounding the ball retraces back its path into the hands of the boy. Then the value of u is :
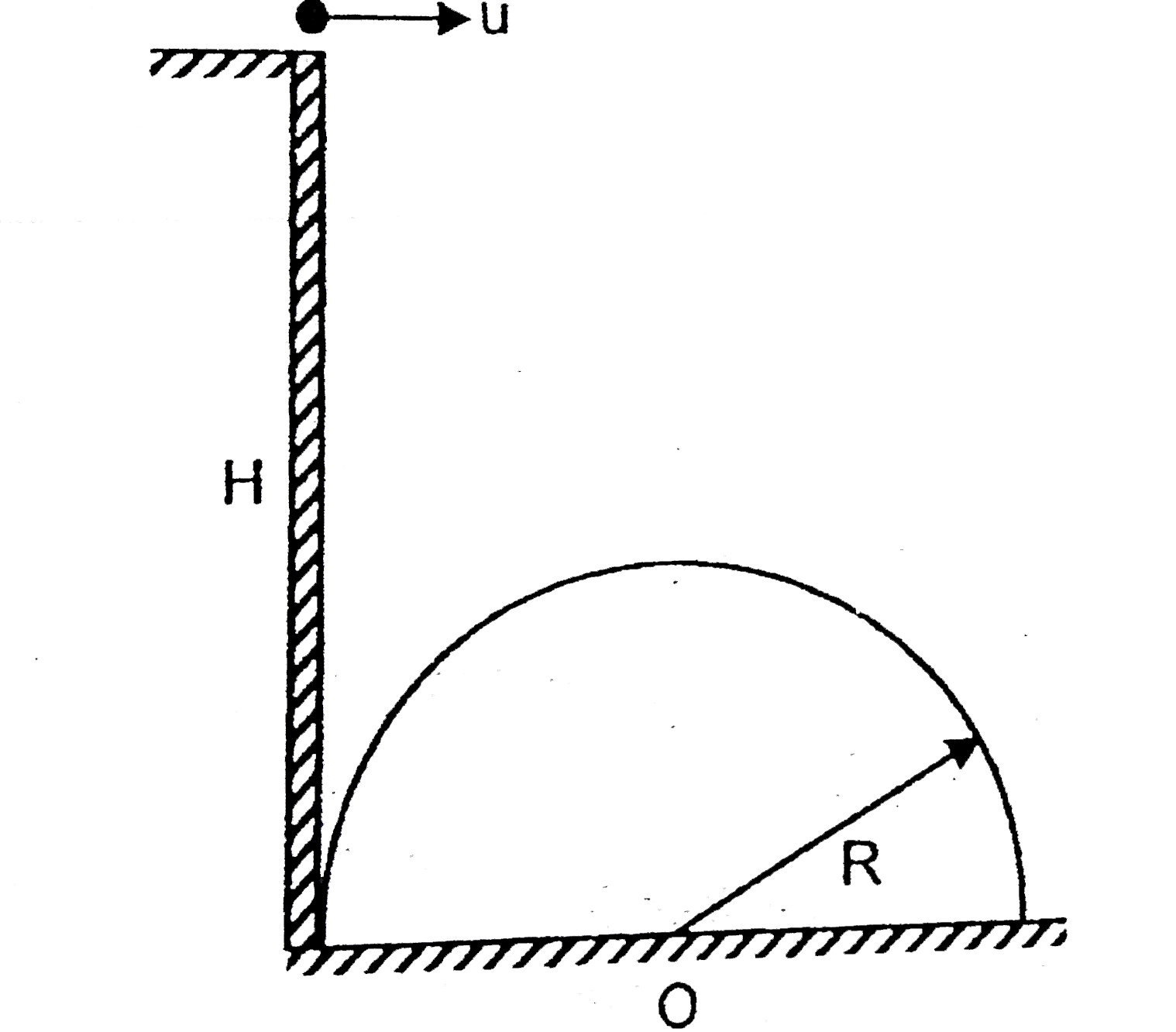
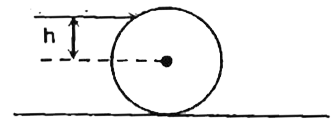
View SolutionIn order to get a billiard ball to roll without sliding from the start, where should the cue hit ? Calculate the height from centre of the sphere. Take R as the radius of sphere.
View SolutionA uniform ball of radius R rolls without slipping between the rails such that the horizontal distance is √3R between the two contact points of te rails of the ball. Figure (a) shows front view of the ball and figure (b) shows the side view of the ball. vCM is the velocity of centre of mass of the ball and ω is the angular velocity of the ball after rolling down a distance 2h along the incline then
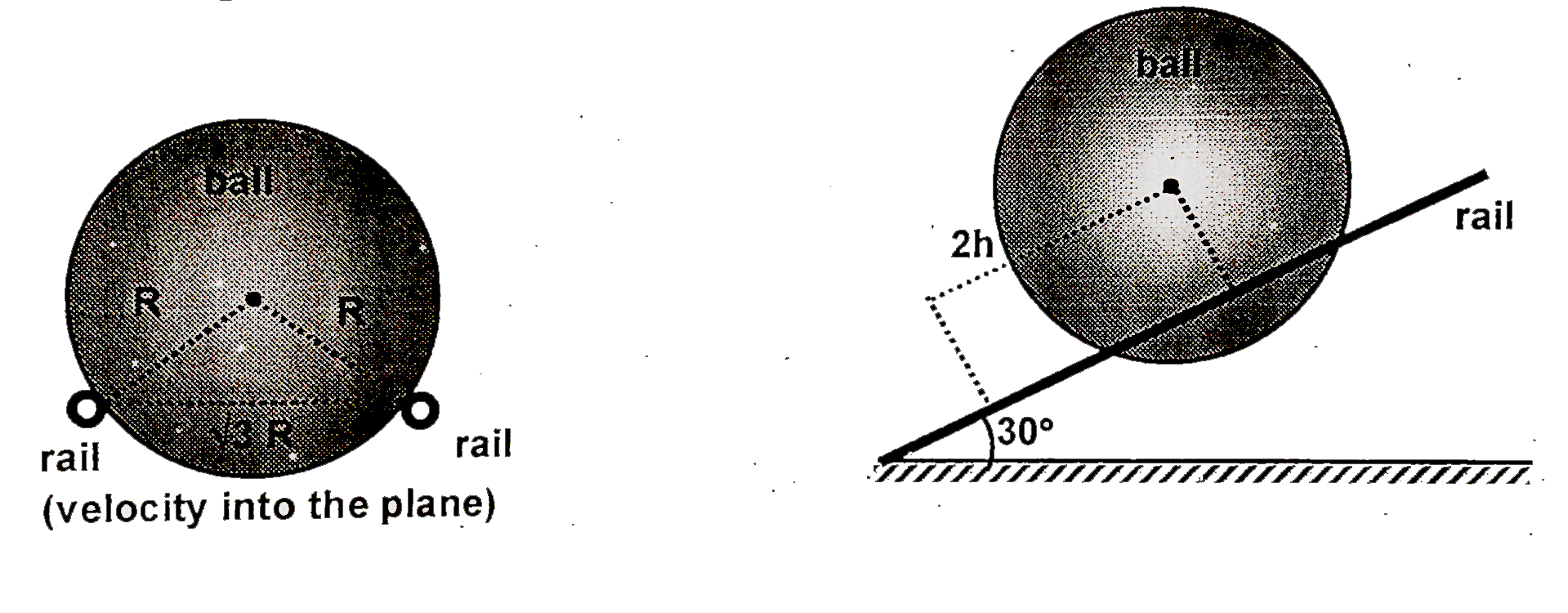
View SolutionTwo friends A and B (each weighing 40kg) are sitting on a frictionless platform some distance d apart. A rolls a ball of mass 4kg on the platform towards B which B catches. Then B rolls the ball towards A and A catches it. The ball keeps on moving back and forth between A and B. The ball has a fixed speed of 5m/s on the platform.
a. Find the speed of A after he rolls the ball for the first time.
b. Find the speed of A after he catches the ball for the first time.
c. Find the speed of A and B after the ball has made five round trips and is held by A.
d. How many times can A roll the ball?
e. Where is the centre of mass of the system A+B+ ball at. the end of the nth trip?
View Solution

