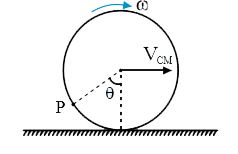
A hoop rolls on a horizontal ground without slipping with liner spped v. Speed of a particle P on the circumference of the hoop at angle θ is 
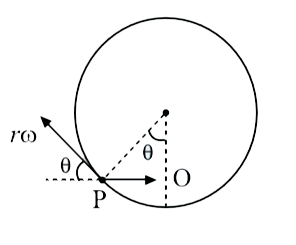
For rolling without slipping, VCM=rω The Velocity of P is the resultant of CM velocity and the tangential velocity rωdue to clockwise rotation velocity of )2=(VCM−rωcosθ)2+(rωsinθ)2=V2CM(1−cosθ)2+V2sin2θ(as rω=VCM=(4V2CMsin2)θ2⇒velocityofP=(2VCMsin)θ2.
Topper's Solved these Questions
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBook:VMC MODULES ENGLISHChapter:SYSTEM OF A PARTICLES & ROTATIONAL MOTIONExercise:SOLVED EXAMPLES
Explore 20 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBook:VMC MODULES ENGLISHChapter:SYSTEM OF A PARTICLES & ROTATIONAL MOTIONExercise:PRACTICE EXERCISE-1
Explore 4 Videos
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:7-previous year question
Explore 46 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:VMC MODULES ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:IMPECCABLE
Explore 56 Videos
Similar Questions
A hoop rolls on a horizontal ground without slipping with linear speed v. Speed of a particle P on the circumference of the hoop at angle θ is :
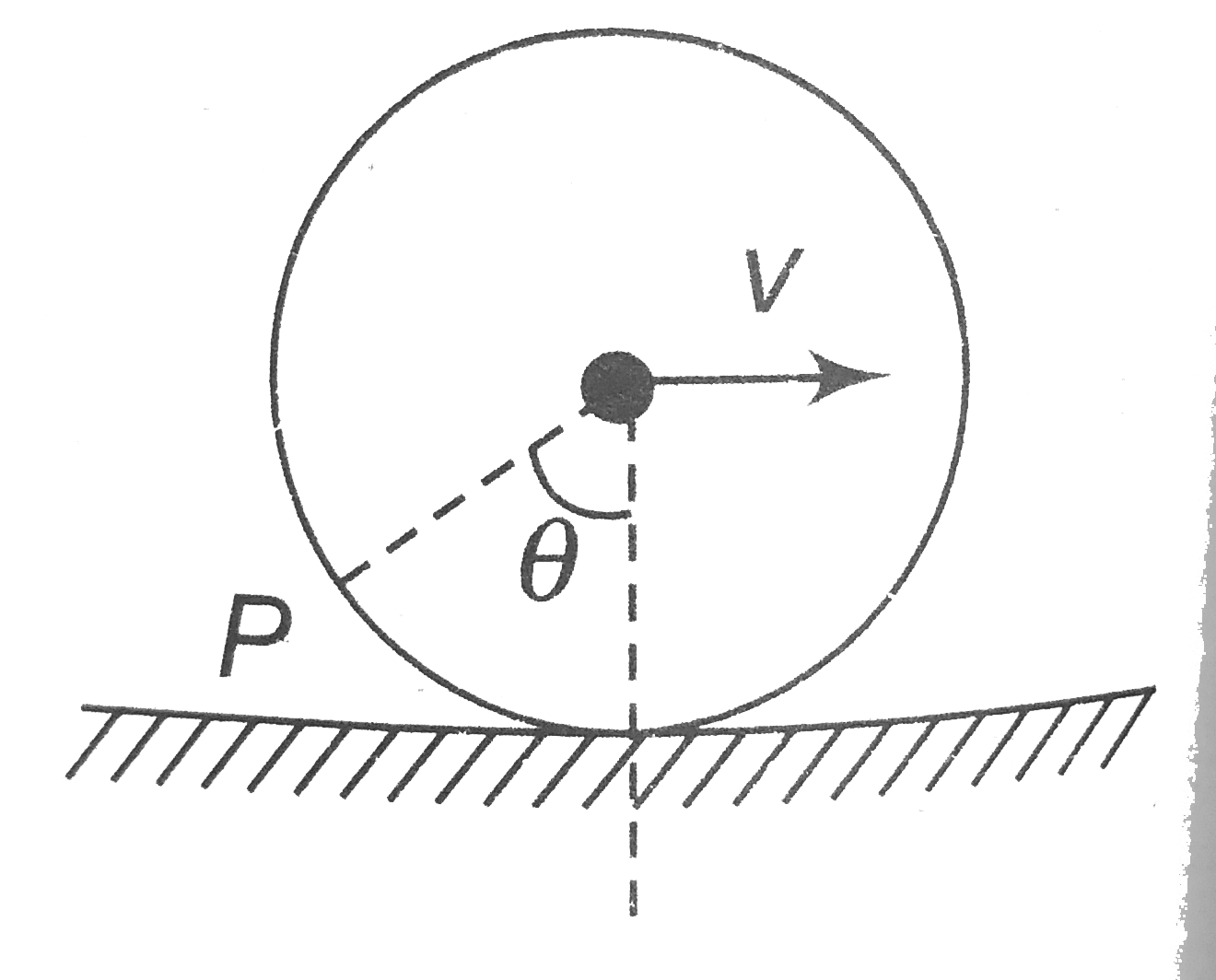
View SolutionA disc rolls on ground without slipping . Velocity of centre of mass is v. There is a point P on circumference of disc at angle θ . Suppose vp is the speed of this point. Then, match the following the following table.

View SolutionA disc rolls on ground without slipping. Velocity of centre of mass is v. There is a point P on circumference of disc at angle θ. Suppose, vP is the speed of this point. Then, match the following columns
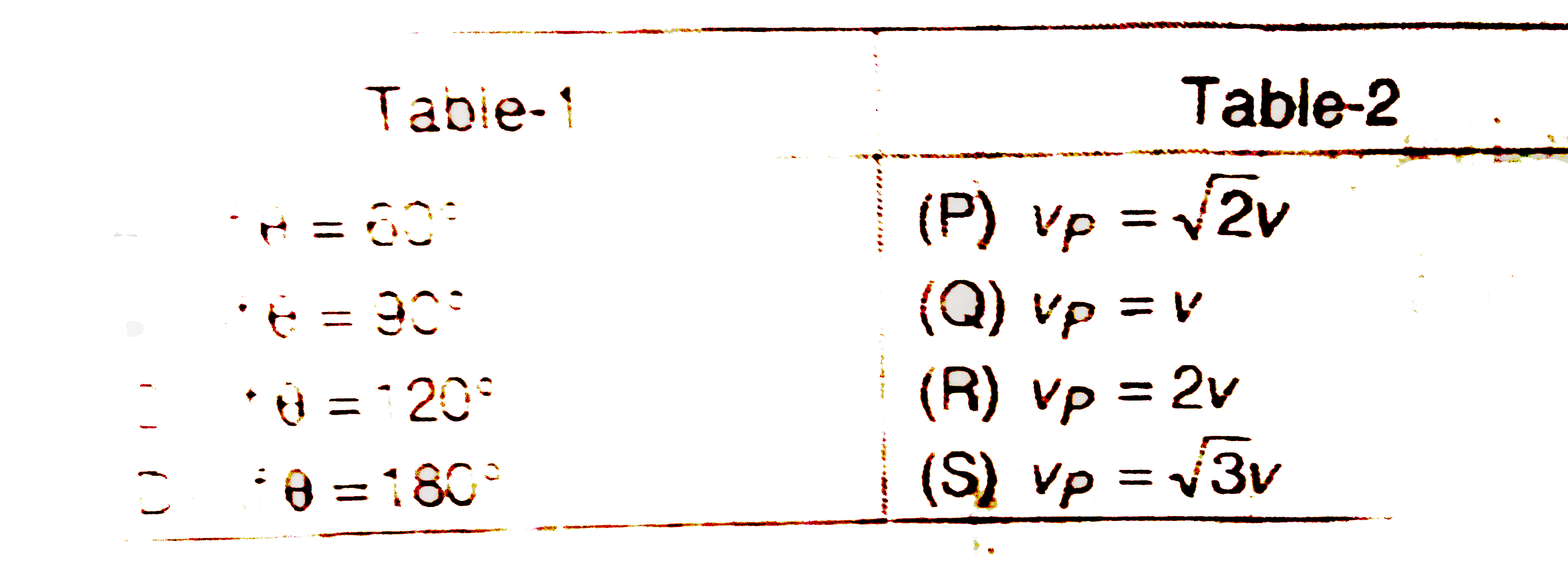
Column-IColumn-II(A)Ifθ=60∘(p)vP=√2v(B)Ifθ=90∘(q)vP=v(C)Ifθ=120∘(r)vP=2vD)Ifθ=180∘(s)vP=√3v
View SolutionA disc rolls over a horizontal floor without slipping with a linear speed of 5 cm/sec. Then the linear speed of a particle on its rim, with respect to the floor, when it is in its highest position is?
View SolutionA smooth hoop lie as on a smooth horizontal table and is fixed. A particle is projected on the table form a point A on the inner circumference of the hoop at angle θ with radius vector . If e be the coefficient of restitution and the particle returns to the point of projection after two successive impacts. The final angle θ' made by velocity vector with radius of hoop is

View SolutionA sphere of mass m and radius r rolls on a horizontal plane without slipping with a speed u. Now it rolls up vertically, then maximum height it would be attain will be
View SolutionThe centre of a wheel rolling without slipping on a plane surface moves with a speed v0. A particle on the rim of the wheel at the same level as the centre of wheel will be moving with speed
View Solution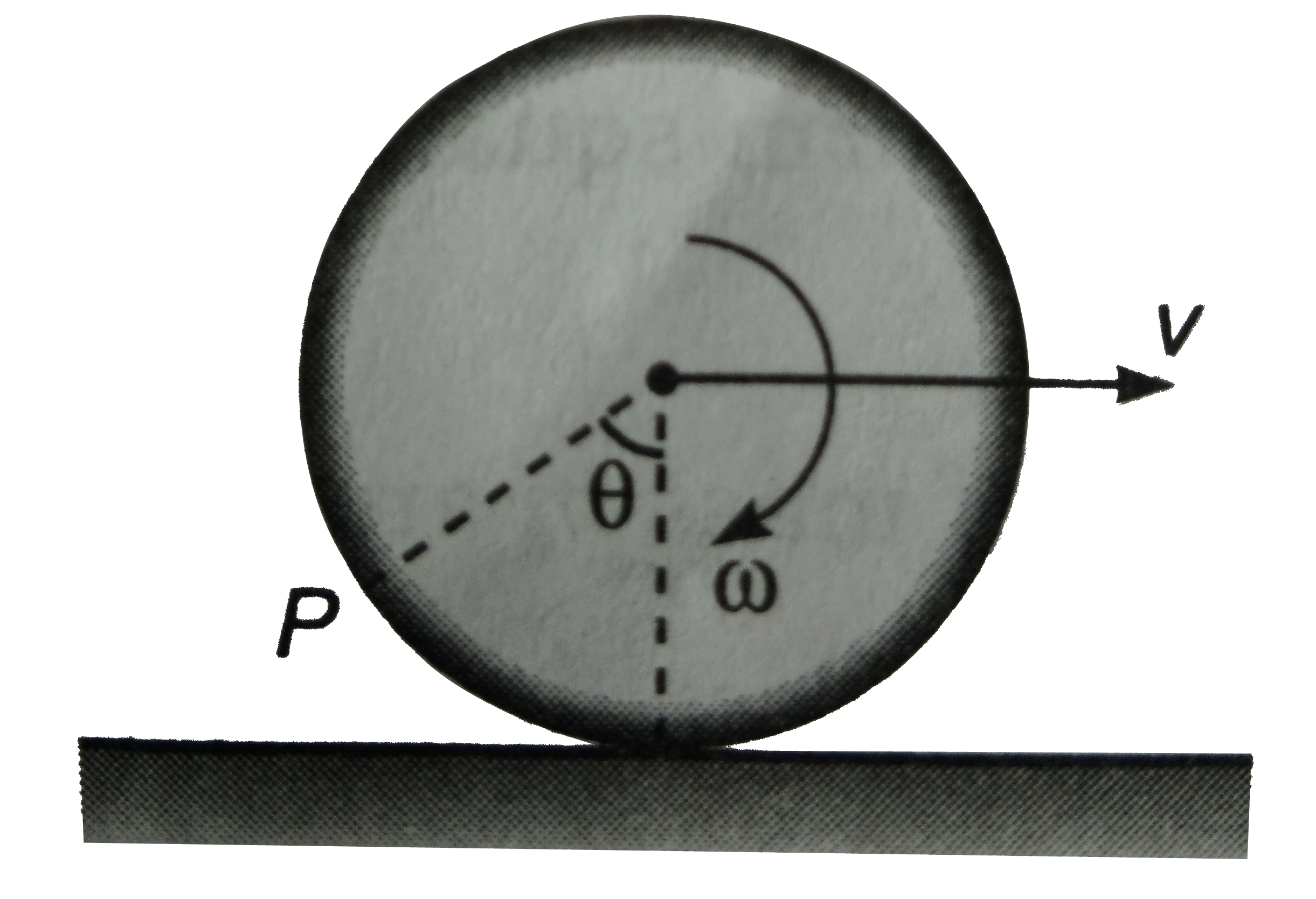
A ring of radius R rolls on a horizontal ground with linear speed v and angular speed ω. For what value of θ the velocity of point P is in vertical direction (v<Rω).
View Solution
A ring of mass m is rolling without slipping with linear speed v as shown in figure. Four particles each of mass m are also attached at points A, B , C and D find total kinetic energy of the system.
View SolutionA thin hoop of mass M and radius r is placed on a horizontal plane. At the initial instant, the hoop is at rest. A small washer of mass m with zero initial velocity slides from the upper point of the hoop along a smooth groove in the inner surfaces of the hoop. Determine the velocity u of the centre of the hoop at the moment when the washer is at a certain point A of the hoop, whose radius vector forms an angle ϕ with the vertical (figure). The friction between the hoop and the plane should be neglected

View Solution