Add vectors →A,→B and →C which have equal magnitude s of 50 unit and are inclined at angles of 45∘,135∘ and 315∘ respectively from x-axos.
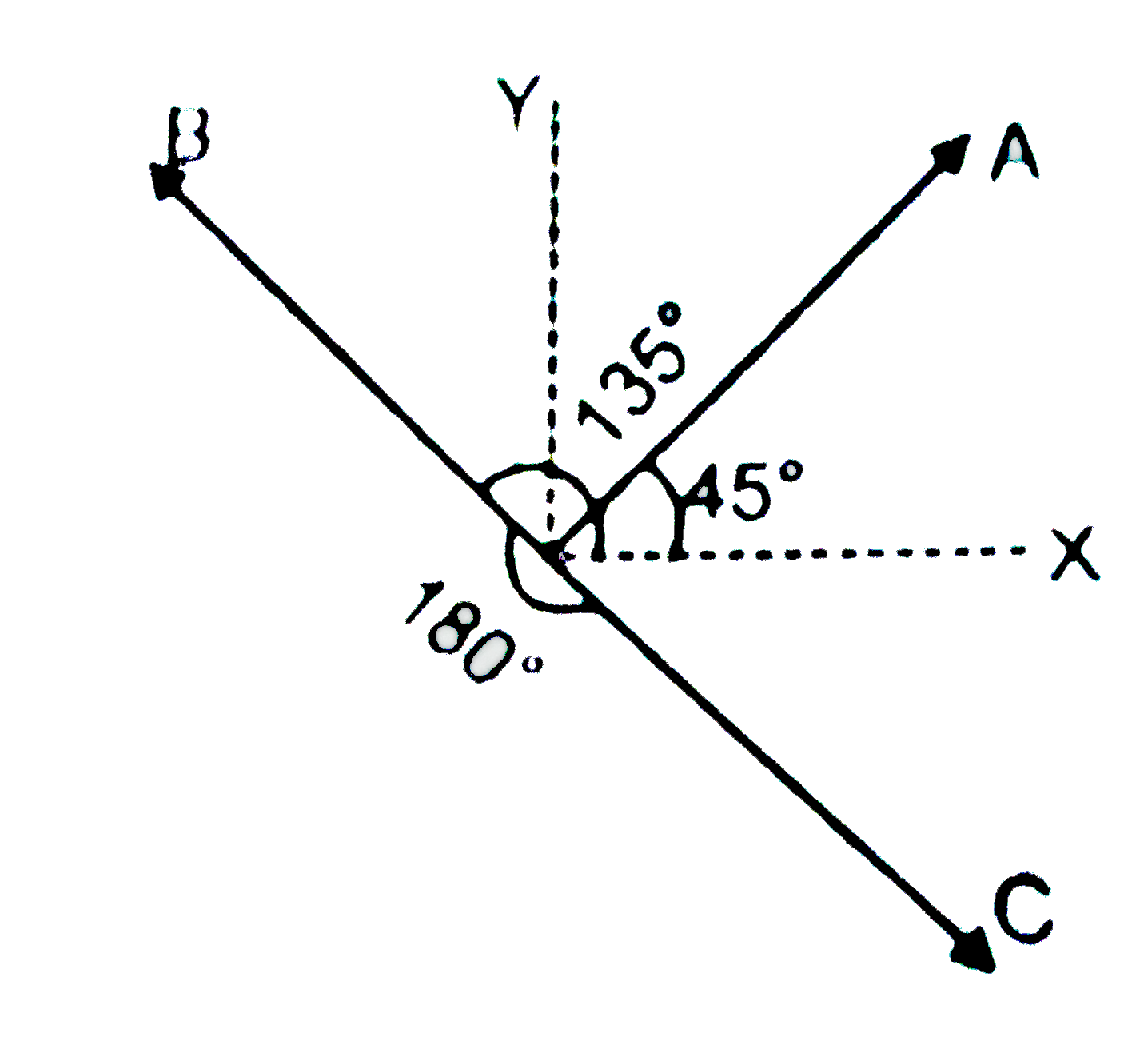
Angle between →Band→C=315∘−135∘=180∘∴ They balance each other so sum of these is →A=50 unit at 45∘ from X-axis
Similar Questions
Knowledge Check
A magnitude of vector →A,→B and →C are respectively 12,5 and 13 units and →A+→B=→C then the angle between →A and →B is
A0Bπ/2Cπ/4Dπ
Let →Aand→B be the two vectors of magnitude 10 unit each. If they are inclined to the X-axis at angles 30∘and60∘ respectively, find the resultant.
View SolutionIf →aand→b are unit vectors inclined to x-axis at angle 30∘and120∘ then ∣∣→a+→b∣∣ equals
View SolutionThree vectors →A,→B and →C are such that →A=→B+→C and their magnitudes are in ratio 5:4:3 respectively. Find angle between vector →A and →C
View SolutionThree vectors →A,→B and →C are such that →A=→B+→C and their magnitudes are in ratio 5:4:3 respectively. Find angle between vector →A and →B
View Solutionif →a,→band→c are mutally perpendicular vectors of equal magnitudes, then find the angle between vectors and →a+→b+→c.
View SolutionTwo vectors →Aand→B have equal magnitudes.If magnitude of (→A+→B) is equal to n times of the magnitude of (→A−→B) then the angle between →Aand→B is :-
View SolutionIf non-zero vectors →aand→b are equally inclined to coplanar vector →c, then →c can be
View Solution
