Question

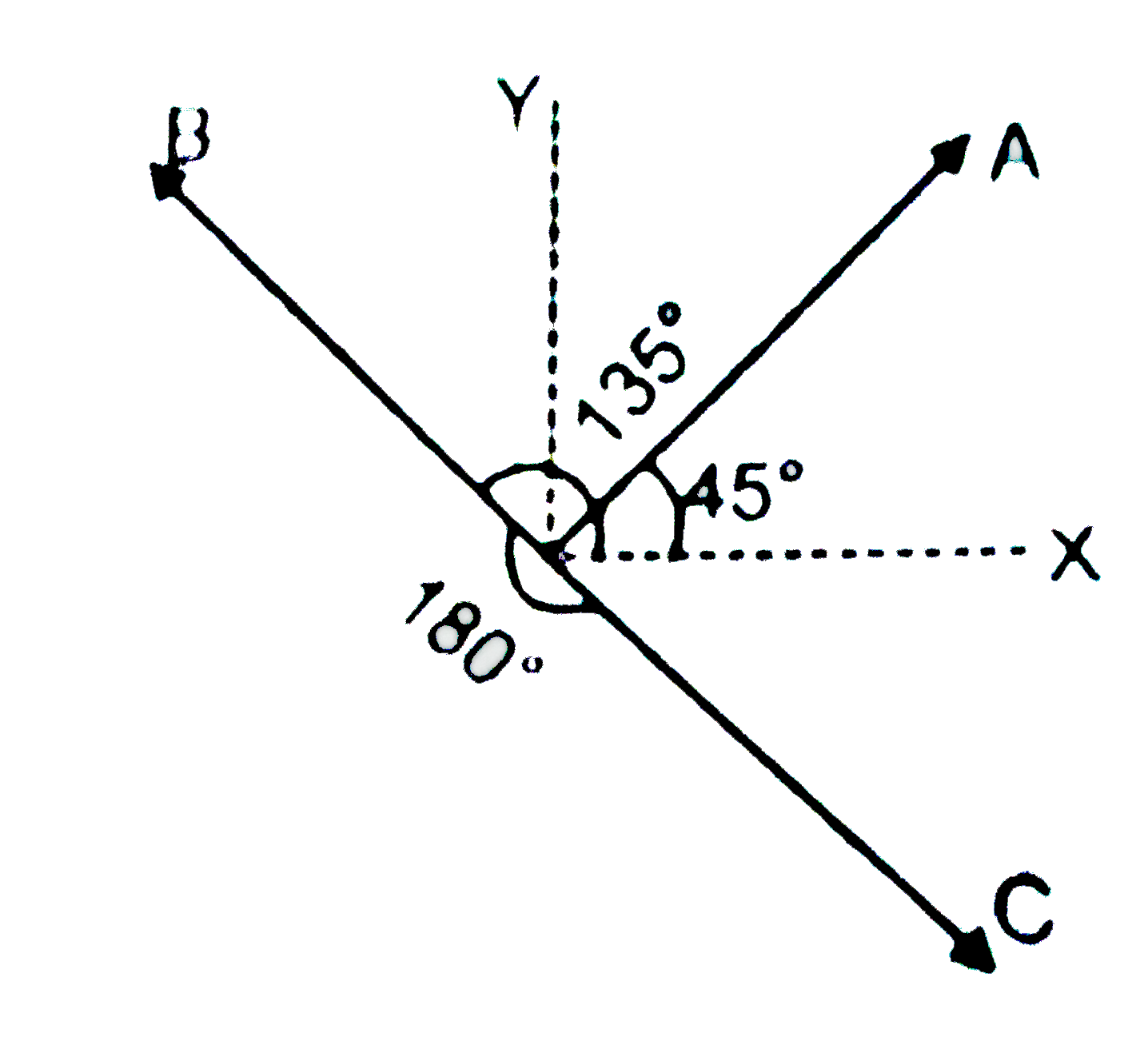
Add vectors $\overrightarrow{A},\overrightarrow{B}\text{and}\overrightarrow{C}$ each having magnitude of 100 unit and inclined to the X-axis at angles ${45}^{\circ },{135}^{\circ }\text{and}{315}^{\circ }$ respectively.

Answer

100 unit at `45^@` with x axis

Explanation

To solve the problem of adding the vectors $$\overrightarrow{A}$$, $$\overrightarrow{B}$$, and $$\overrightarrow{C}$$ with magnitudes of 100 units and angles of $${45}^{\circ }$$, $${135}^{\circ }$$, and $${315}^{\circ }$$ respectively, we can follow these steps:

Step 1: Break down each vector into its components
We will use the formula for the components of a vector:
\( \vec{V} = V_x \hat{i} + V_y \hat{j} \)
where \(V_x = V \cos(\theta)\) and \(V_y = V \sin(\theta)\).

1. For \(\vec{A}\):
- Magnitude = 100 units, Angle = \(45^\circ\)
\( A_x = 100 \cos(45^\circ) = 100 \times \frac{\sqrt{2}}{2} = 50\sqrt{2} \)
\( A_y = 100 \sin(45^\circ) = 100 \times \frac{\sqrt{2}}{2} = 50\sqrt{2} \)
Thus, \(\vec{A} = 50\sqrt{2} \hat{i} + 50\sqrt{2} \hat{j}\).

2. For \(\vec{B}\):
- Magnitude = 100 units, Angle = \(135^\circ\)
\( B_x = 100 \cos(135^\circ) = 100 \times -\frac{\sqrt{2}}{2} = -50\sqrt{2} \)
\( B_y = 100 \sin(135^\circ) = 100 \times \frac{\sqrt{2}}{2} = 50\sqrt{2} \)
Thus, \(\vec{B} = -50\sqrt{2} \hat{i} + 50\sqrt{2} \hat{j}\).

3. For \(\vec{C}\):
- Magnitude = 100 units, Angle = \(315^\circ\)
\( C_x = 100 \cos(315^\circ) = 100 \times \frac{\sqrt{2}}{2} = 50\sqrt{2} \)
\( C_y = 100 \sin(315^\circ) = 100 \times -\frac{\sqrt{2}}{2} = -50\sqrt{2} \)
Thus, \(\vec{C} = 50\sqrt{2} \hat{i} - 50\sqrt{2} \hat{j}\).

Step 2: Sum the components of the vectors
Now, we will add the components of the vectors:

- Sum of x-components:
\( R_x = A_x + B_x + C_x = (50\sqrt{2}) + (-50\sqrt{2}) + (50\sqrt{2}) = 50\sqrt{2} \)

- Sum of y-components:
\( R_y = A_y + B_y + C_y = (50\sqrt{2}) + (50\sqrt{2}) + (-50\sqrt{2}) = 50\sqrt{2} \)

Step 3: Resultant vector
The resultant vector \(\vec{R}\) can be expressed as:
\( \vec{R} = R_x \hat{i} + R_y \hat{j} = 50\sqrt{2} \hat{i} + 50\sqrt{2} \hat{j} \)

Step 4: Magnitude of the resultant vector
To find the magnitude of the resultant vector:
\( |\vec{R}| = \sqrt{R_x^2 + R_y^2} = \sqrt{(50\sqrt{2})^2 + (50\sqrt{2})^2} = \sqrt{2500 \times 2 + 2500 \times 2} = \sqrt{5000} = 100\sqrt{5} \)

Conclusion
The resultant vector \(\vec{R}\) has a magnitude of \(100\sqrt{5}\) units, and it is directed at an angle \(\theta\) with respect to the x-axis given by:
\( \tan(\theta) = \frac{R_y}{R_x} = \frac{50\sqrt{2}}{50\sqrt{2}} = 1 \implies \theta = 45^\circ \)

Final Result
Thus, the resultant vector has a magnitude of \(100\sqrt{5}\) units and is directed at an angle of \(45^\circ\) with respect to the x-axis.

---