A Wheatstone network consists of four resistances (in cyclic order) 10Ω,5Ω,6Ω,6Ω . The resistance that must be connected across the 10Ωresistance so that the network becomes balanced is (in Ohm):
10
5
20
6
To solve the problem of finding the resistance that must be connected across the 10Ω resistor in a Wheatstone network to make it balanced, we can follow these steps:
1. Understand the Wheatstone Bridge Configuration:
The Wheatstone bridge consists of four resistors arranged in a diamond shape. The resistors are given as follows:
- R1 = 10Ω (across which we need to connect a resistor)
- R2 = 5Ω
- R3 = 6Ω
- R4 = 6Ω
2. Set Up the Balance Condition:
For the Wheatstone bridge to be balanced, the following condition must hold true:
R1R2=R3R4
In our case, we need to find the equivalent resistance (R_eq) that will be connected across the 10Ω resistor.
3. Use the Balance Condition:
We can express the balance condition as:
R3⋅Req=R4⋅R2
Plugging in the values:
6⋅Req=6⋅5
4. Solve for R_eq:
Simplifying the equation:
6⋅Req=30
Req=306=5Ω
5. Determine the Type of Connection:
Since we need to connect this equivalent resistance (5Ω) across the 10Ω resistor, we need to connect it in parallel.
6. Calculate the Required Resistance (R):
We can use the formula for resistors in parallel:
1Req=1R+110
Substituting Req=5Ω:
15=1R+110
7. Solve for R:
Rearranging gives:
1R=15−110
Finding a common denominator (10):
1R=210−110=110
Therefore:
R=10Ω
Final Answer:
The resistance that must be connected across the 10Ω resistor to balance the Wheatstone network is 10Ω.
---
The Wheatstone bridge consists of four resistors arranged in a diamond shape. The resistors are given as follows:
- R1 = 10Ω (across which we need to connect a resistor)
- R2 = 5Ω
- R3 = 6Ω
- R4 = 6Ω
For the Wheatstone bridge to be balanced, the following condition must hold true:
R1R2=R3R4
In our case, we need to find the equivalent resistance (R_eq) that will be connected across the 10Ω resistor.
We can express the balance condition as:
R3⋅Req=R4⋅R2
Plugging in the values:
6⋅Req=6⋅5
Simplifying the equation:
6⋅Req=30
Req=306=5Ω
Since we need to connect this equivalent resistance (5Ω) across the 10Ω resistor, we need to connect it in parallel.
We can use the formula for resistors in parallel:
1Req=1R+110
Substituting Req=5Ω:
15=1R+110
Rearranging gives:
1R=15−110
Finding a common denominator (10):
1R=210−110=110
Therefore:
R=10Ω
The resistance that must be connected across the 10Ω resistor to balance the Wheatstone network is 10Ω.
Topper's Solved these Questions
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-1 DAILY TUTORIAL SHEET -5
15 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-2 DAILY TUTORIAL SHEET-1
10 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-1 DAILY TUTORIAL SHEET-3
15 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-F
10 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
31 Videos
Similar Questions
Knowledge Check
In a Wheatstone's network, P=2Ω,Q=2Ω,R=2ΩandS=3Ω. The resistance with which S is to be shunted in order that the bridge may be balanced is
 A1ΩB2ΩC4ΩD6Ω
A1ΩB2ΩC4ΩD6ΩThe correct combination of three resistances 1Ω,2Ωand3Ω to get equivalent resistance 115Ω is
AAll three are combines in paralleBAll three are combines in paralleC1Ωand2Ω in parallel and 3Ω is in series to bothD2Ωand3Ω in parallel and 3Ω is in series to both
Find the current l through then 10Ω resistance in the network shown in figure.
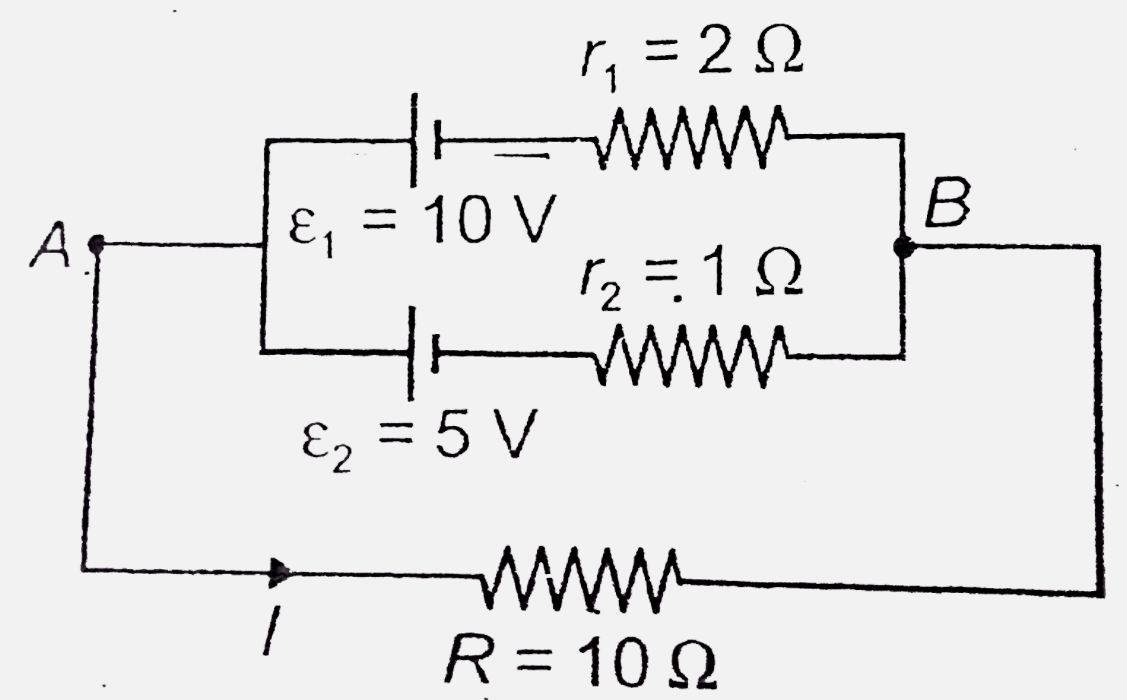
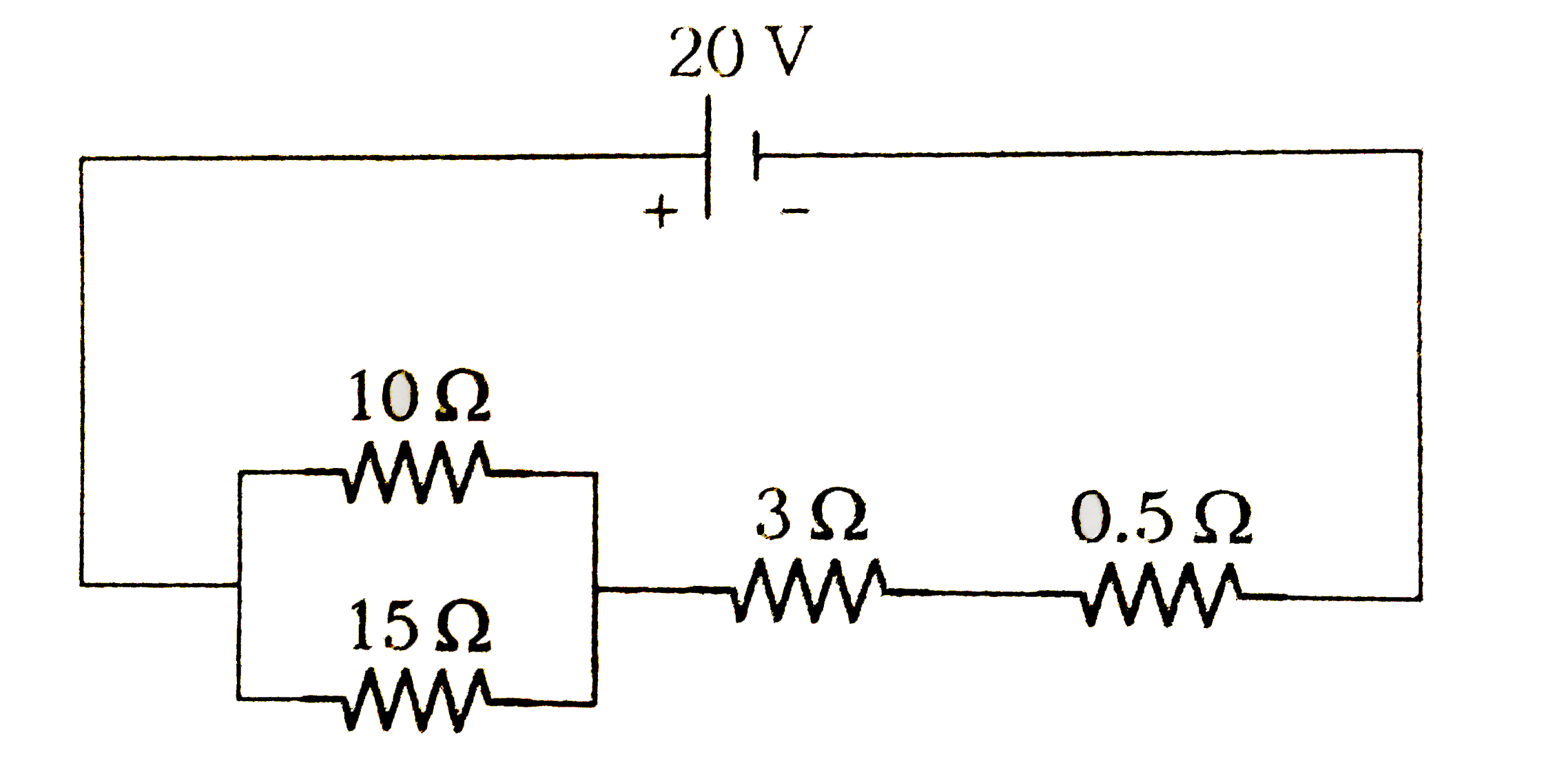
View SolutionIn the circuit, the current flowing through 10Ω resistance is
View SolutionIn Wheatstone bridge, four resistors of resistances 15Ω,12Ω,4Ω and 10Ω respectively, are connected in cyclic order. The resistance ( in Ω) that is to be connected in parallel with the resistance of 10Ω to balance the network is
View SolutionAn infinite ladder network of resistances is constructed with 1Ωand2Ω resistances as shown

View SolutionFind the current through the 10Ω resistance connected across AB
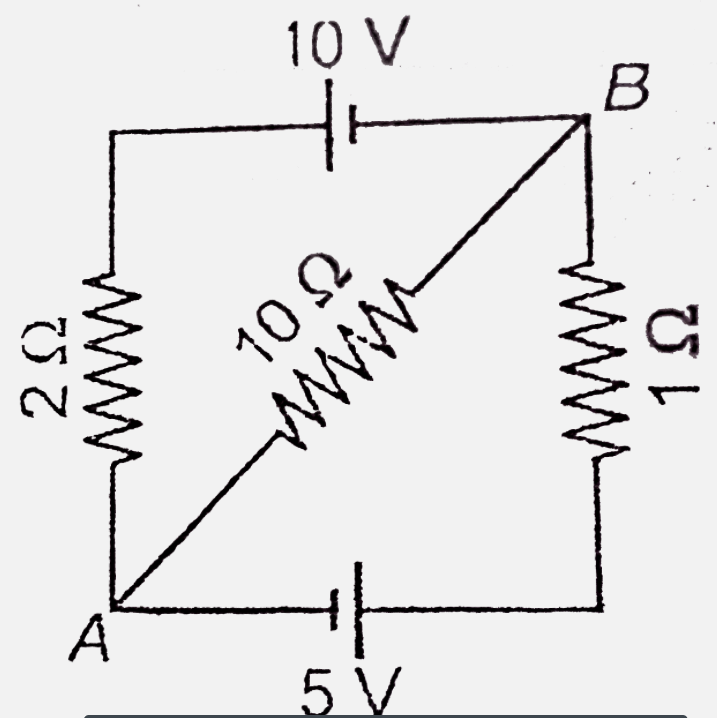
View SolutionThe resistance of a conductor is 5Ω at 50∘C and 6Ω at 100∘C. The resistance at 0∘C is
View Solution

