Two long wires are placed parallel to each other with a distance 1 m between them. The wires carry equal current 1 A in the same direction. The magnetic field intensity at a point P which is equidistant from the wires is 1.6×10−7T. Then, the distance of this point from any one of the wires is _________ m.
[Permeability of vacuum, μ0=4π×10−7T−m/A]
The correct Answer is:A
To solve the problem, we need to find the distance x from point P to either of the wires. Here’s a step-by-step solution:
Step 1: Understand the Configuration
We have two long parallel wires separated by a distance of 1 meter, each carrying a current of 1 A in the same direction. The point P is equidistant from both wires.
Step 2: Define the Distance
Let the distance from point P to either wire be x. Since the total distance between the two wires is 1 meter, we can express this as:
x+x=1or2x=1
Thus, x=0.5 m. However, we need to find the magnetic field intensity at point P.
Step 3: Magnetic Field Due to a Long Straight Wire
The magnetic field intensity B at a distance r from a long straight wire carrying current I is given by:
B=μ0I2πr
where μ0 is the permeability of free space.
Step 4: Calculate the Total Magnetic Field at Point P
Since point P is equidistant from both wires, the magnetic field contributions from both wires at point P will add up. Therefore, the total magnetic field B at point P is:
B=B1+B2=μ0I2πx+μ0I2πx=2μ0I2πx=μ0Iπx
Step 5: Substitute the Given Values
We know:
- B=1.6×10−7T
- I=1A
- μ0=4π×10−7T⋅m/A
Substituting these values into the equation:
1.6×10−7=(4π×10−7)⋅1πx
Step 6: Simplify the Equation
The π cancels out:
1.6×10−7=4×10−7x
Step 7: Solve for x
Rearranging gives:
x=4×10−71.6×10−7
Calculating this:
x=41.6=2.5m
Final Answer
The distance of point P from either of the wires is:
2.5m
We have two long parallel wires separated by a distance of 1 meter, each carrying a current of 1 A in the same direction. The point P is equidistant from both wires.
Let the distance from point P to either wire be x. Since the total distance between the two wires is 1 meter, we can express this as:
x+x=1or2x=1
Thus, x=0.5 m. However, we need to find the magnetic field intensity at point P.
The magnetic field intensity B at a distance r from a long straight wire carrying current I is given by:
B=μ0I2πr
where μ0 is the permeability of free space.
Since point P is equidistant from both wires, the magnetic field contributions from both wires at point P will add up. Therefore, the total magnetic field B at point P is:
B=B1+B2=μ0I2πx+μ0I2πx=2μ0I2πx=μ0Iπx
We know:
- B=1.6×10−7T
- I=1A
- μ0=4π×10−7T⋅m/A
1.6×10−7=(4π×10−7)⋅1πx
The π cancels out:
1.6×10−7=4×10−7x
Rearranging gives:
x=4×10−71.6×10−7
Calculating this:
x=41.6=2.5m
The distance of point P from either of the wires is:
2.5m
Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Main (Archive)
75 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Advanced (Archive)
78 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - LEVEL 1
75 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)
55 Videos
- MOCK TEST 1BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 1EXERCISE - PART I : PHYSICS (SECTION-2)
10 Videos
Similar Questions
Two wires are held perpendicular to the plane of paper and are 5 m apart. They carry currents of 2.5 A and 5 A in same direction. Then, the magnetic field strength (B) at a point midway between the wires will be
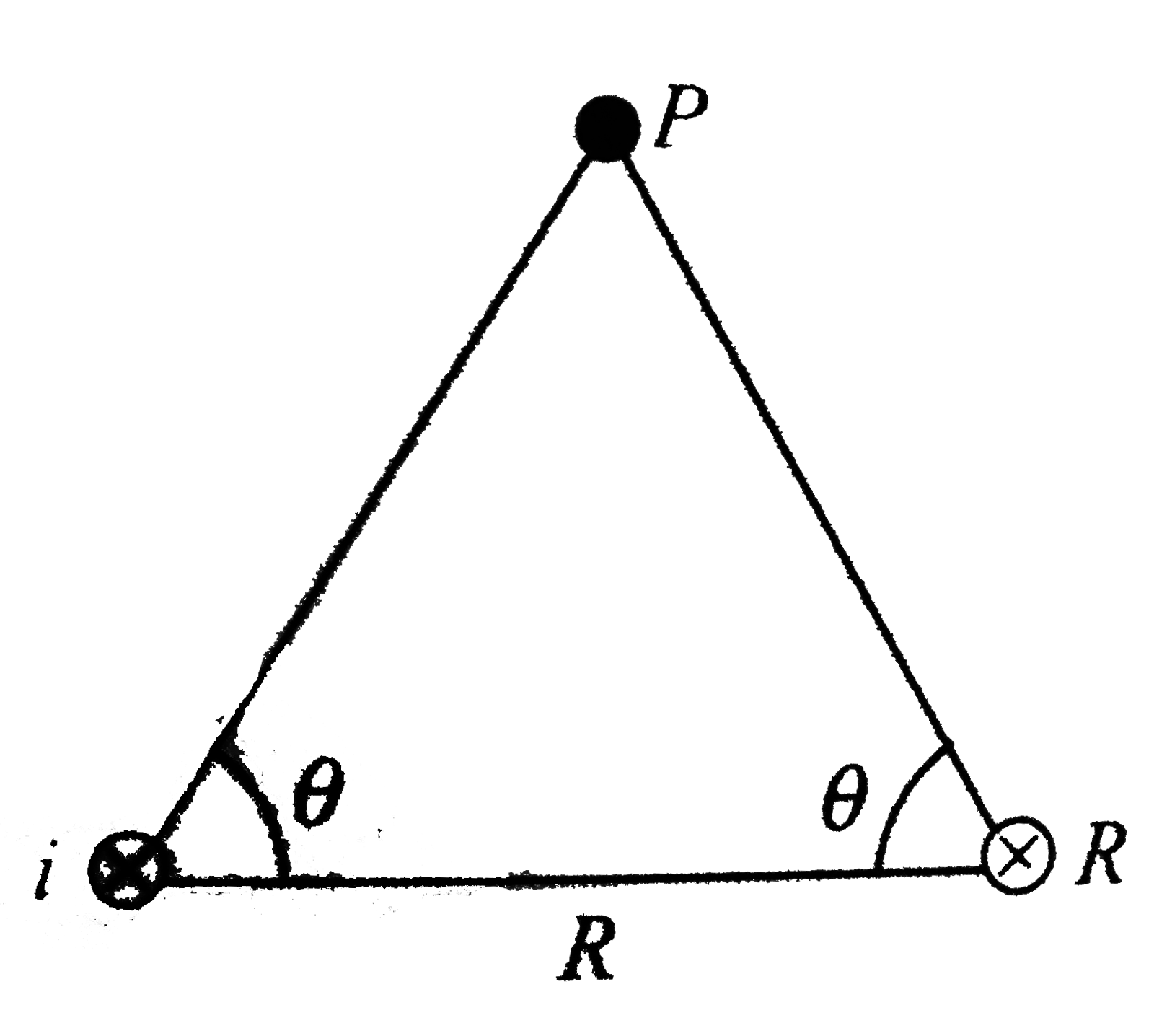
View SolutionIn Fig. two long parallel wires (seen end-on) that are a distance R apart carry equal currents i in the same sense. Find the magnitude of the magnetic field at point P , which lies quidistant from the two wires at an angle θ from the plane of the wires.
View SolutionTwo long straight wires are set parallel to each other Each carries a current i in the same direction and the separation between them is 2r. The intensity of the magnetic field midway between them is
View SolutionTwo infinite, parallel wires are a distance 10 cm apart and carry equal current 20 A in the same direction. The magnetic force on a 1 cm long segment of one wire due to the other wire is ___________ ×10−6N. (Permeabilityi of vacuum μ0=4π×10−7N/A2)
View SolutionTwo long straight wires are set parallel to each other. Each carriers a current i in the same direction and the separation between them is 2r. The intensity of the magnetic field midway between them is

View SolutionTwo parallel wires carry equal currents of 10A along the same direction and are separated by a distance of 2.0 cm. Find the magnetic field at a point which is 2.0 cm away from each of these wires.
View SolutionTwo long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
View SolutionTwo infinitely long straight parallel wires carry equal currents 'I' in the same direction and are 2 m apart. Magnetic induction at a point which is at same normal distance (√2)m from each wire has magnitude
View SolutionA long wire carries a current of 4.00 A. Find the energy stored in the magnetic field inside a volume of 1.0mm3 at a distance of 10.0 cm from the wire.
View SolutionThe magnetic field at a distance r from a long wire carryimg current I is 0.4 T. The magnetic field at a distance 2r is
View Solution
