A metal ring of radius r=0.5m with its plane normal a unifrom magnetic field B of induction 0.2T carries a current I=100A The tension in newtons developed in the ring is
(a)100
(b)50
(c)25
(d)10
The correct Answer is:D
To solve the problem of finding the tension developed in the metal ring, we will follow these steps:
Step 1: Understand the setup
We have a metal ring of radius r=0.5m placed in a uniform magnetic field B=0.2T. The ring carries a current I=100A.
Step 2: Calculate the magnetic force on the ring
The magnetic force F on a current-carrying conductor in a magnetic field can be calculated using the formula:
F=I⋅L⋅B⋅sin(θ)
where:
- I is the current,
- L is the length of the conductor,
- B is the magnetic field strength,
- θ is the angle between the direction of the current and the magnetic field.
In this case, the current flows around the ring, and the magnetic field is perpendicular to the plane of the ring, so θ=90∘ and sin(90∘)=1.
Step 3: Calculate the length of the ring
The length L of the ring (which is the circumference of the circle) is given by:
L=2πr=2π×0.5=πm
Step 4: Substitute values into the force equation
Now substituting the values into the force equation:
F=I⋅L⋅B=100A⋅πm⋅0.2T
F=100⋅π⋅0.2=20πN
Step 5: Calculate the tension in the ring
The tension T in the ring must balance the total magnetic force acting on the ring. Since the force acts uniformly around the ring, we can relate the total magnetic force to the tension:
2T=F
Thus,
T=F2=20π2=10πN
Step 6: Final answer
Using the approximate value of π≈3.14:
T≈10×3.14=31.4N
Conclusion
The tension developed in the ring is approximately 31.4N.
---
We have a metal ring of radius r=0.5m placed in a uniform magnetic field B=0.2T. The ring carries a current I=100A.
The magnetic force F on a current-carrying conductor in a magnetic field can be calculated using the formula:
F=I⋅L⋅B⋅sin(θ)
where:
- I is the current,
- L is the length of the conductor,
- B is the magnetic field strength,
- θ is the angle between the direction of the current and the magnetic field.
The length L of the ring (which is the circumference of the circle) is given by:
L=2πr=2π×0.5=πm
Now substituting the values into the force equation:
F=I⋅L⋅B=100A⋅πm⋅0.2T
F=100⋅π⋅0.2=20πN
The tension T in the ring must balance the total magnetic force acting on the ring. Since the force acts uniformly around the ring, we can relate the total magnetic force to the tension:
2T=F
Thus,
T=F2=20π2=10πN
Using the approximate value of π≈3.14:
T≈10×3.14=31.4N
The tension developed in the ring is approximately 31.4N.
Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Main (Archive)
75 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Advanced (Archive)
78 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - LEVEL 1
75 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)
55 Videos
- MOCK TEST 1BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 1EXERCISE - PART I : PHYSICS (SECTION-2)
10 Videos
Similar Questions
A thin circular -conducting ring having N turns of radius R is falling with its plane vertical in a horizontal magnetic field B . At the position MNQ the speed of ring is v the induced e.m.f developed across the ring is
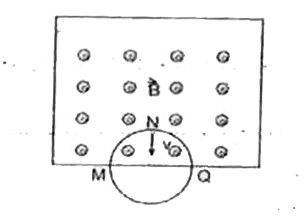
View SolutionA ring of mass (2π)kg and of radius 0.25m is making 300rpm about an axis through its perpendicular to its plane. The tension in newton developed in ring is approximately a) 50 b) 100 c) 175 d) 247
View SolutionA metallic ring of area 25cm2 is placed perpendicular to a magnetic field of 0.2T.Its is removed from the field in 0.2s.Find the average emf produced in the ring during this time.
View SolutionA Conducting ring of radius 1 meter is placed in an uniform magnetic field B of 0.01 tesla oscillating with frequency 100Hz with its plane at right angles to B. What will be the induced electric field?
View SolutionA circular flexible loop of wire of radius r carrying a current I is placed in a uniform magnetic field B . If B is doubled, then tension in the loop
View SolutionA thin semi-circular conducting ring of radius R is falling with its plane verticle in horizontal magnetic induction (→B). At the position MNQ the speed of the ring is v, and the potential difference developed across the ring is
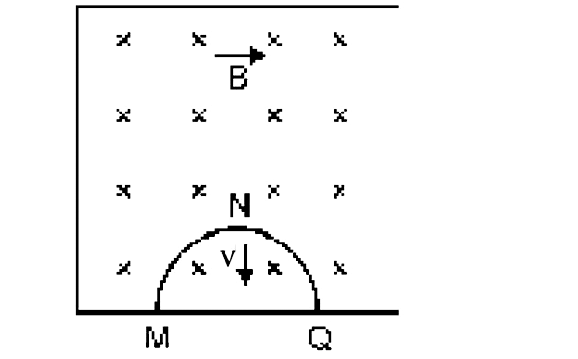
View SolutionThe figure shows a conducting ring of radius R. A uniform steady magnetic field B lies perpendicular to the plane of the ring a circular region r(<R). If the resistance per unit length of the ring is λ, then the current induced in the ring when its radius gets doubled is

View SolutionA conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
View SolutionA thin semicircular conducting ring of radius R is falling with its plane verticle in a horizontal magnetic inducting B. At the position MNQ, the speed of the ring is V and the potential difference developed across the ring is

(1.) zero
(2.)BcπR2/2
(3.) πRBV
(4.) 2RBV
View SolutionIf plane of coil and uniform magnetic field B(4T0 is same then torque on the current carrying coil is

View Solution
