There exists a long conductor along z-axis carrying a current of I0 along positive z-direction. A loop having total resistance R is placed symmetrical about x- and y-axes in xy plane as shown in figure. potential difference vBA=V is applied. Radii of arcs are ‘a’ and ‘b’, respectively, as shown in the figure. The magnitude of force experienced by the arc MN is :
zero
μ0VI0πRb
μ0VI02πRb
None of these
The correct Answer is:A
To solve the problem of finding the magnitude of the force experienced by the arc MN in the given setup, we can follow these steps:
Step 1: Understand the Setup
We have a long straight conductor along the z-axis carrying a current I0 in the positive z-direction. There is also a loop in the xy-plane that is symmetrical about the x- and y-axes. The potential difference VBA=V is applied across the loop, which has arcs of radii a and b.
Hint: Visualize the setup and identify the direction of the current and the magnetic field produced by the straight conductor.
Step 2: Determine the Magnetic Field
Using the right-hand rule, we can determine the direction of the magnetic field B produced by the straight conductor. The magnetic field around a long straight conductor carrying current is given by:
B=μ0I02πr
where r is the distance from the conductor to the point where we want to calculate the magnetic field.
Hint: Remember that the magnetic field circles around the conductor and its direction depends on the direction of the current.
Step 3: Analyze the Current in the Arc MN
The potential difference VBA applied across the loop causes a current I to flow through the loop. The direction of this current can be determined based on the potential difference. If VA is at a higher potential than VB, the current will flow from A to B.
Hint: Use Ohm's law to relate the potential difference, current, and resistance: I=VR.
Step 4: Calculate the Force on Arc MN
The force F experienced by a current-carrying conductor in a magnetic field is given by:
F=IL×B
where L is the length vector of the current element and B is the magnetic field vector. The magnitude of the force can be expressed as:
F=B⋅I⋅L⋅sin(θ)
In this case, since the magnetic field B is perpendicular to the current I flowing through the arc MN, we need to consider the angle θ.
Hint: If the current direction is opposite to the magnetic field direction, θ could be 180∘, leading to sin(180∘)=0.
Step 5: Conclusion
Since sin(180∘)=0, the force experienced by the arc MN is:
F=B⋅I⋅L⋅0=0
Thus, the magnitude of the force experienced by the arc MN is 0 Newtons.
Final Answer: The correct option is 0.
We have a long straight conductor along the z-axis carrying a current I0 in the positive z-direction. There is also a loop in the xy-plane that is symmetrical about the x- and y-axes. The potential difference VBA=V is applied across the loop, which has arcs of radii a and b.
Using the right-hand rule, we can determine the direction of the magnetic field B produced by the straight conductor. The magnetic field around a long straight conductor carrying current is given by:
The potential difference VBA applied across the loop causes a current I to flow through the loop. The direction of this current can be determined based on the potential difference. If VA is at a higher potential than VB, the current will flow from A to B.
The force F experienced by a current-carrying conductor in a magnetic field is given by:
Since sin(180∘)=0, the force experienced by the arc MN is:
Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Main (Archive)
75 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Advanced (Archive)
78 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - LEVEL 1
75 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)
55 Videos
- MOCK TEST 1BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 1EXERCISE - PART I : PHYSICS (SECTION-2)
10 Videos
Similar Questions
There exists a long conductor along z-axis carrying a current I0 along positive z-direction. A loop having total resistance R is placed symmetrical about x-axis and y-axes in x-y plane as shown in Fig. potential difference VBA=V is applied. Radii of arcs are a and b, respectively, as shown in the figure.
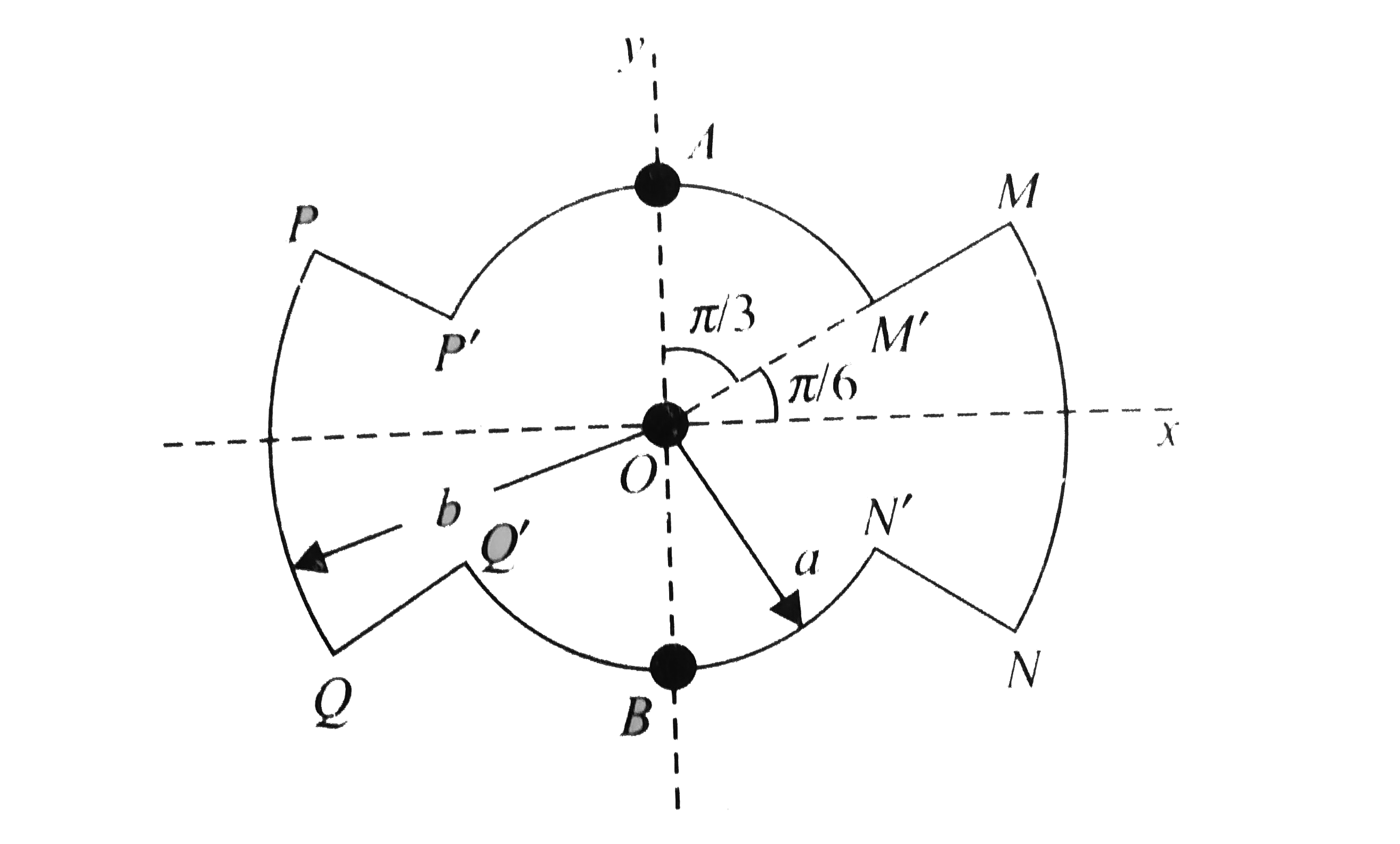
The magnitude of force experienced by the arc MN is
View SolutionThere exists a long conductor along z-axis carrying a current I0 along positive z-direction. A loop having total resistance R is placed symmetrical about x-axis and y-axes in x-y plane as shown in Fig. potential difference VBA=V is applied. Radii of arcs are a and b, respectively, as shown in the figure.
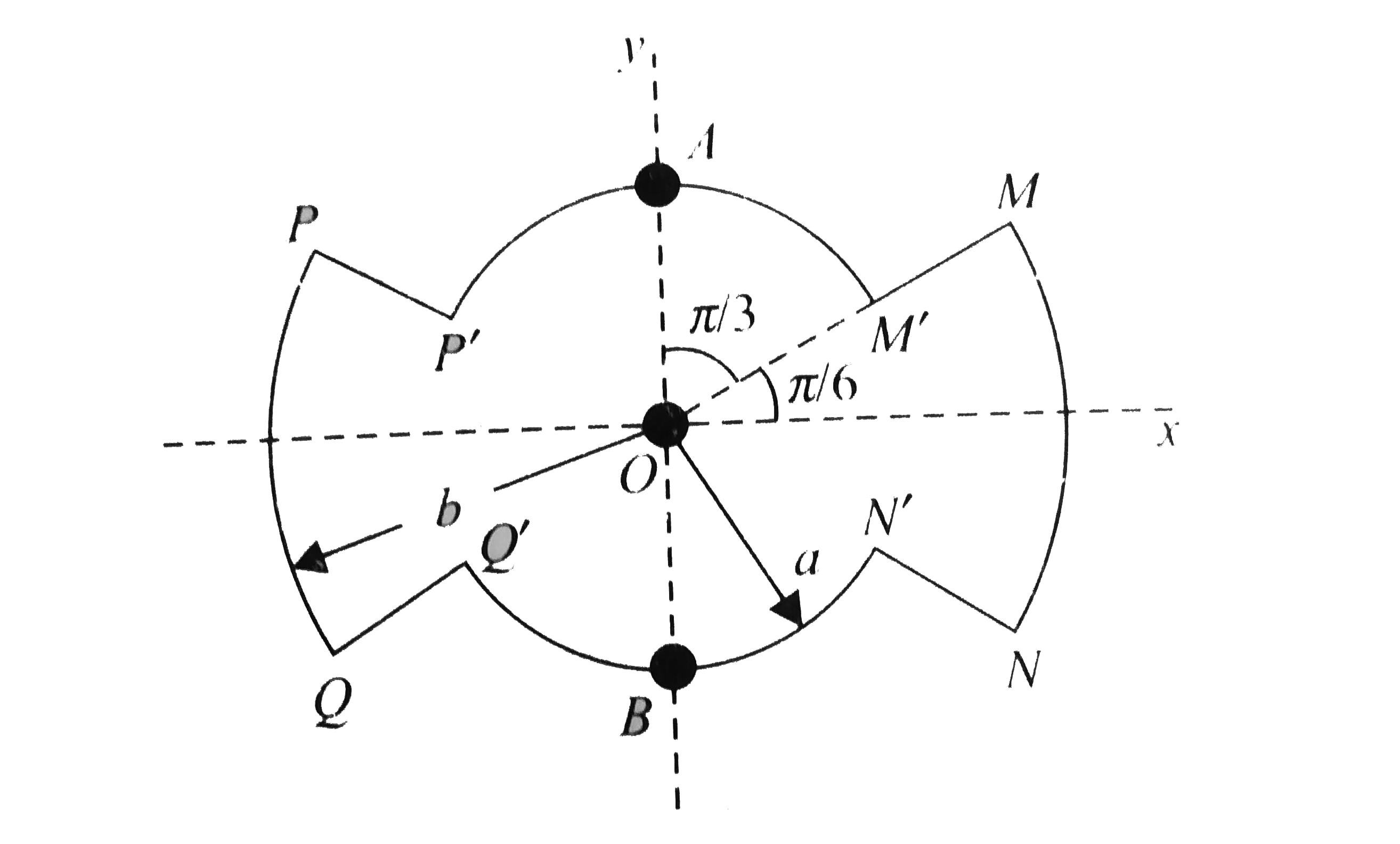
The total torque acting on the loop is nearly
View SolutionThe uniform electric field is along positive y-axis positive x axis as shown in figure. The signs of potential differences VP−VQ and VB−VA respectively are
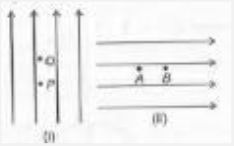
View SolutionA long straight wire along the z- axis carries a current I in the negative z−direction . The magnetic vector field →B at a point having coordinates (x,y) in the Z=0 plane is
View SolutionA long straight wire along the z- axis carries a current I in the negative z−direction . The magnetic vector field →B at a point having coordinates (x,y) in the Z=0 plane is
View SolutionA circular loop of radius R=20 cm is placed in a uniform magnetic field B=2T in xy-plane as shown in figure. The loop carries a current i=1.0A in the direction shown in figure. Find the magnitude of torque acting on the loop.

View SolutionA circular loop of radius R=20 cm is placed in a uniform magnetic field B=2T in xy-plane as shown in figure. The loop carries a current i=1.0A in the direction shown in figure. Find the magnitude of torque acting on the loop.

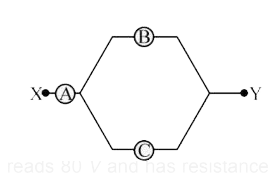
View SolutionThree voltmeters A, B and C having resistances R, 1.5 R and 3 R respectively are used in a circuit as shown. When a potential difference is applied between X and Y, the readings of the voltmeters are V1,V2andV3respectively. Then :
View SolutionA long straight wire is kept along x-axis. It carries a current i in the positive x-direction. A proton and an electron are placed at (0, a,0) and (0, -a, 0) respecitively. The proton is imparted an initial velocity v along +z axis and the electron is imparted an initial velocity v along +x-axis. The magnetic forces experienced by the two particles at the instant are
View SolutionA ring of the radius R is placed in the y - z plane and it carries a current i. The conducting wires which are used to supply the current to the ring can be assumed to be vary long and are placed as shown in the figure. The magnitude of the magnetic field at the centre of the ring A is
View Solution
