A particle of mass M and charge Q moving with velocity →v describe a circular path of radius R when subjected to a uniform transverse magnetic field of induction B. The work done by the field when the particle completes one full circle is
(a)(mv2R)2πR
(b)zero
(c)BQ2πR
(d)BQv2R
The correct Answer is:B
Force is perpendicular to displacement.

⇒ Work done →F.→d=0
Related Playlists
- BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - LEVEL 250videos
MAGNETIC EFFECTS OF CURRENT
- BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Main (Archive)75videos
MAGNETIC EFFECTS OF CURRENT
- BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - LEVEL 0 (LONG ANSWER TYPE )3videos
MAGNETIC EFFECTS OF CURRENT
- BOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)55videos
LIQUIDS
- BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 1EXERCISE - PART I : PHYSICS (SECTION-2)10videos
MOCK TEST 1
Similar Questions
An electron is moving on a circular path of radius r with speed v in a transverse magnetic field B. e/m for it will be
View SolutionA particle of mass m and charge Q moving with a velocity v enters a region on uniform field of induction B Then its path in the region is s
View SolutionThe path of a charged particle moving in a uniform steady magnetic field cannot be a
View SolutionA particle of mass m, charge q and kinetic energy T enters in a transverse uniform magnetic field of induction B. After the 3 s, the kinetic energy of the particle will be
View SolutionA charged particle of mass m is moving with a speed u in a circle of radius r. If the magnetic field induction at the centre is B, the charge on the particle is
View SolutionA charged particle of mass m and charge q travels on a circular path of radius r that is perpendicular to a magnetic field B. The time takeen by the particle to complete one revolution is
View SolutionA particle of mass m having a charge q enters into a circular region of radius R with velocity v directed towards the centre. The strength of magnetic field is B. Find the deviation in the path of the particle.
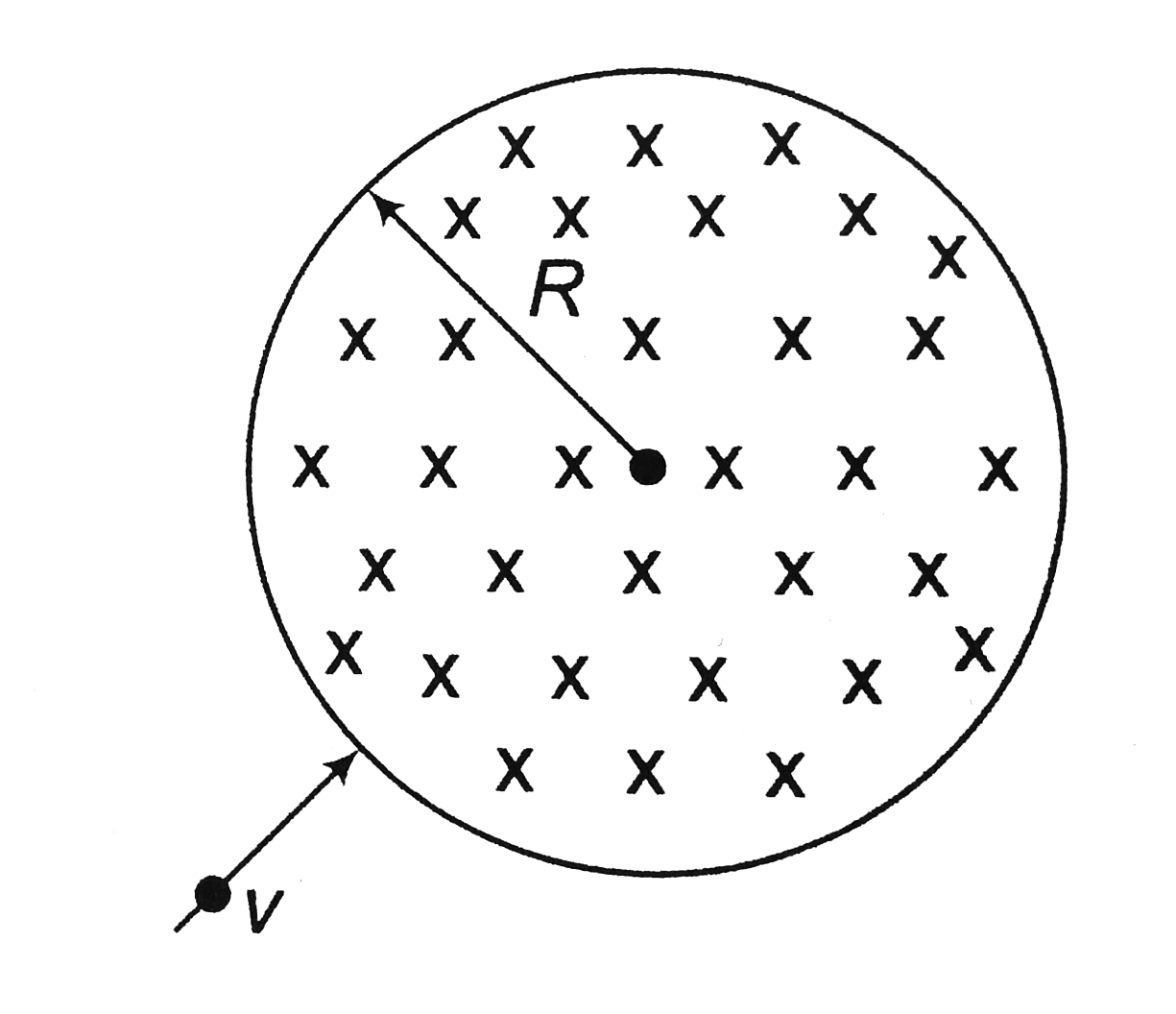 View Solution
View SolutionWhen a charged particle enters a uniform magnetic field its kinetic energy
View SolutionWhen a charged particle moving with velocity →v is subjected to a magnetic field of induction →B, the force on it is non-zero. This implies that:
View SolutionA charged particle of mass m and charge q describes circular motion of radius r in a uniform magnetic field of strength B the frequency of revolution is
View Solution


