The displacement-time graph for two particles A and B are straight lines inclined at angles of 30∘ and 60∘ with the time axis. The ratio of velocities of VA:VB is
1:2
1:√3
√3:1
1:3
The correct Answer is:D
To solve the problem of finding the ratio of the velocities of two particles A and B based on their displacement-time graphs, we can follow these steps:
Step 1: Understand the relationship between slope and velocity
The slope of a displacement-time graph represents the velocity of the particle. Therefore, if we have two angles, θ_A for particle A and θ_B for particle B, we can express their velocities in terms of the slopes of their respective graphs.
Step 2: Write the formula for the ratio of velocities
The ratio of the velocities of particles A and B can be expressed as:
VAVB=slope of Aslope of B
Step 3: Relate the slope to the angle
The slope of the displacement-time graph can be calculated using the tangent of the angle:
slope=tan(θ)
Thus, we can rewrite the ratio of velocities as:
VAVB=tan(θA)tan(θB)
Step 4: Substitute the given angles
We are given:
- θ_A = 30°
- θ_B = 60°
Substituting these values into the equation gives:
VAVB=tan(30°)tan(60°)
Step 5: Calculate the tangent values
Using the known values of tangent:
- tan(30°)=1√3
- tan(60°)=√3
Substituting these values into the equation:
VAVB=1√3√3=13
Step 6: Express the ratio in simplest form
This can be simplified to:
VAVB=13⇒VA:VB=1:3
Final Answer
Thus, the ratio of the velocities of particles A and B is:
1:3
---
The slope of a displacement-time graph represents the velocity of the particle. Therefore, if we have two angles, θ_A for particle A and θ_B for particle B, we can express their velocities in terms of the slopes of their respective graphs.
The ratio of the velocities of particles A and B can be expressed as:
VAVB=slope of Aslope of B
The slope of the displacement-time graph can be calculated using the tangent of the angle:
slope=tan(θ)
Thus, we can rewrite the ratio of velocities as:
VAVB=tan(θA)tan(θB)
We are given:
- θ_A = 30°
- θ_B = 60°
VAVB=tan(30°)tan(60°)
Using the known values of tangent:
- tan(30°)=1√3
- tan(60°)=√3
VAVB=1√3√3=13
This can be simplified to:
VAVB=13⇒VA:VB=1:3
Thus, the ratio of the velocities of particles A and B is:
1:3
Topper's Solved these Questions
- KINEMATICS OF A PARTICLE Book:VMC MODULES ENGLISHChapter:KINEMATICS OF A PARTICLE Exercise:LEVEL 2
Explore 65 Videos
- KINEMATICS OF A PARTICLE Book:VMC MODULES ENGLISHChapter:KINEMATICS OF A PARTICLE Exercise:JEE MAIN (archive)
Explore 19 Videos
- KINEMATICS OF A PARTICLE Book:VMC MODULES ENGLISHChapter:KINEMATICS OF A PARTICLE Exercise:JEE Advanced (archive)
Explore 14 Videos
- JEE MAIN REVISON TEST-23Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISON TEST-23Exercise:PHYSICS (SECTION 2)
Explore 1 Video
- LAWS OF MOTION Book:VMC MODULES ENGLISHChapter:LAWS OF MOTION Exercise:IMPECCABLE
Explore 53 Videos
Similar Questions
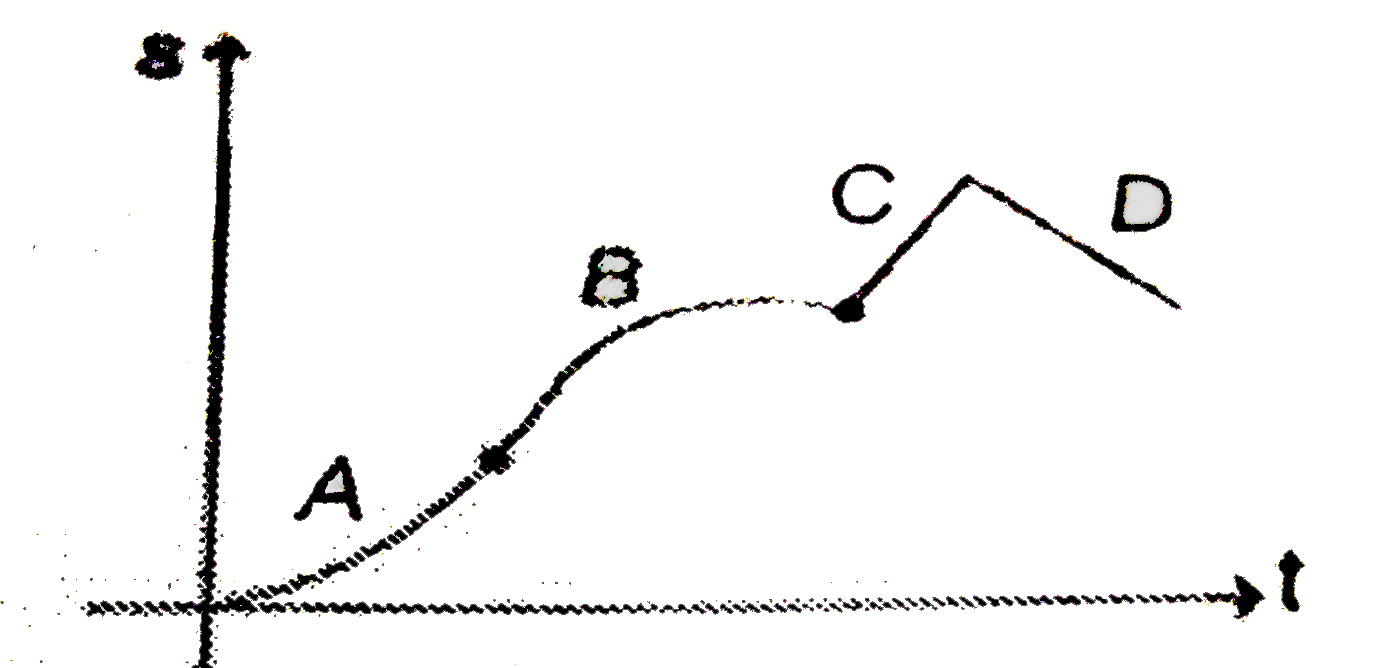
Displacement time graph of a particle moving in a straight line is a shown in figure.
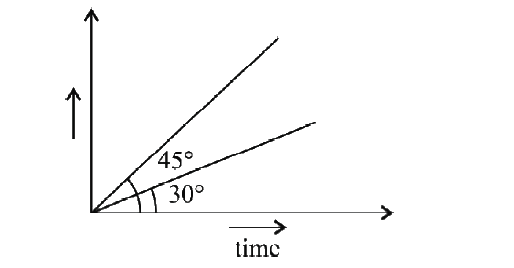
View SolutionThe displacement time graph of two moving particles make angles of 30∘ and 45∘ with the x-axis. The ratio of the two velocities VAandVB is
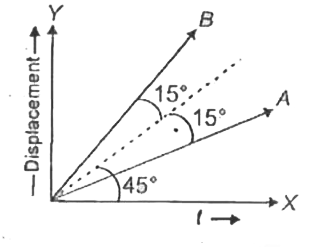
View SolutionThe displacement - time graph for two particles A and B is as follows. The ratio vAvB is
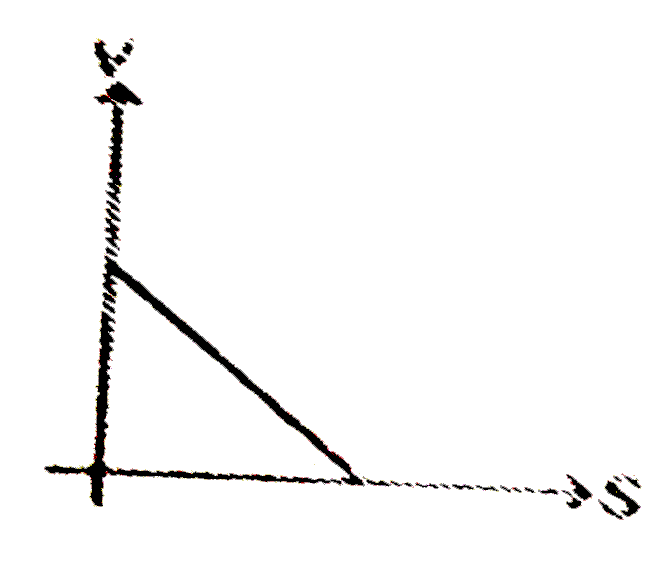
View SolutionVelocity displacement graph of a particle moving in a straight line is as shown in figure.
View SolutionThe displacement-time graphs of two particles P and Q are as shown in the figure. The ratio of their velocities VP and VQ will be
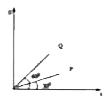
View Solution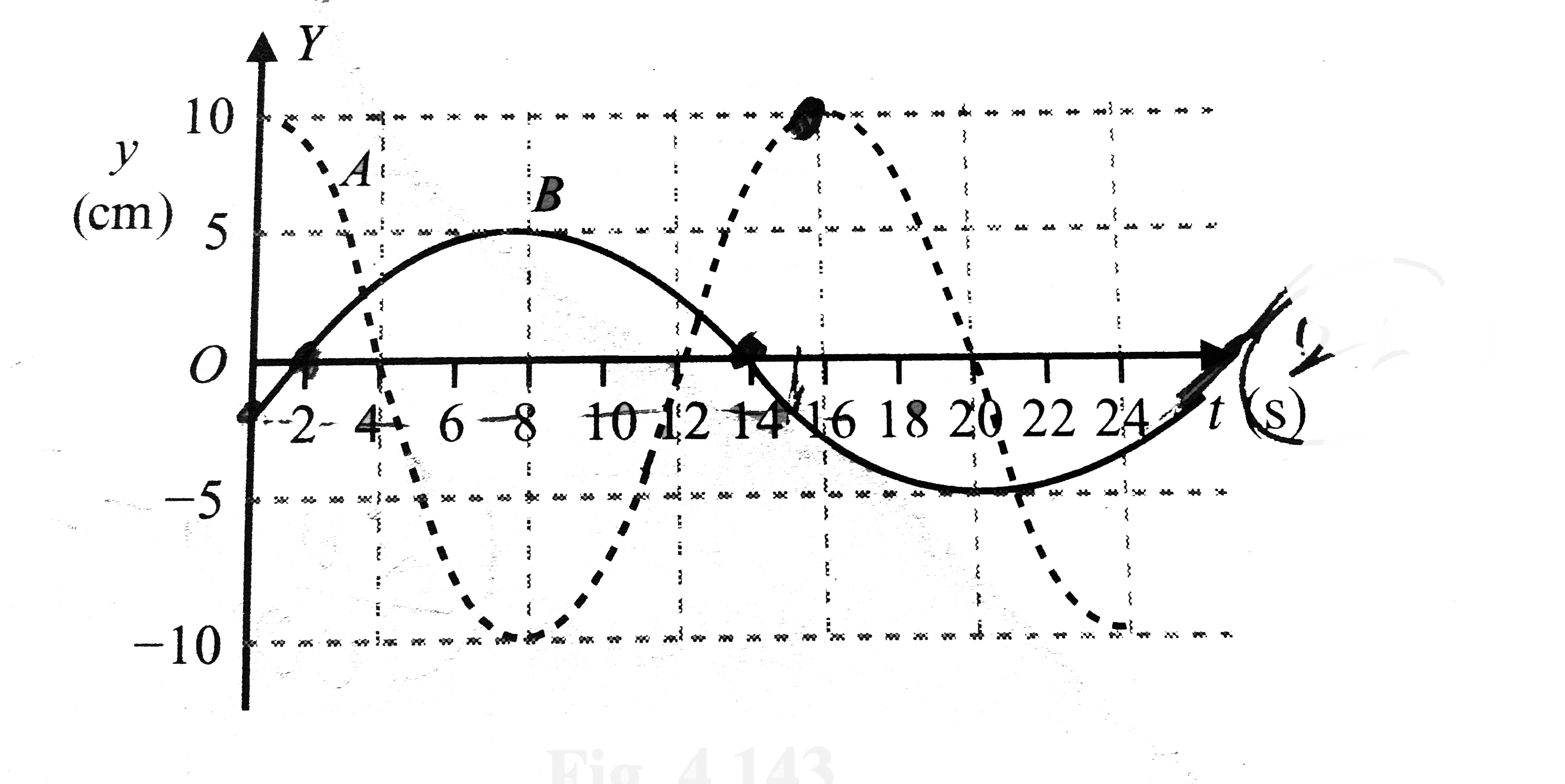
The following figure shows the displacement versus time graph for two particles A and B executing simple harmonic motions. The ratio of their maximum velocities is
View SolutionThe position-time graph of a moving particle is a straight line inclined with time axis and passing through origin, therefore
View Solution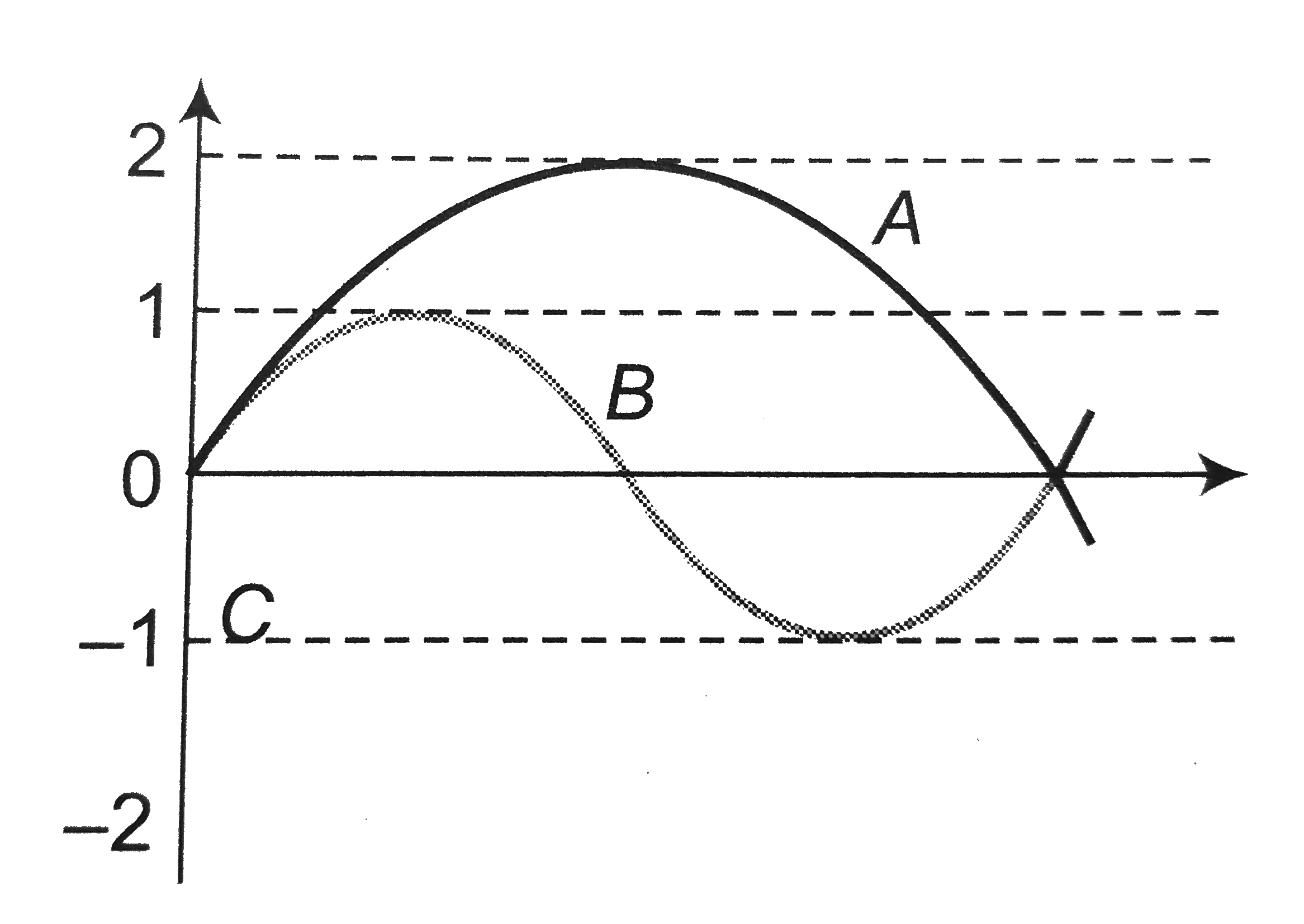
The displacement time graph for two sound waves A and B are shown in the figure. Then the ratio of their intensities IA/IB is equal to
View Solution
The displacement time graph for two sound waves A and B are shown in the figure. Then the ratio of their intensities IA/IB is equal to
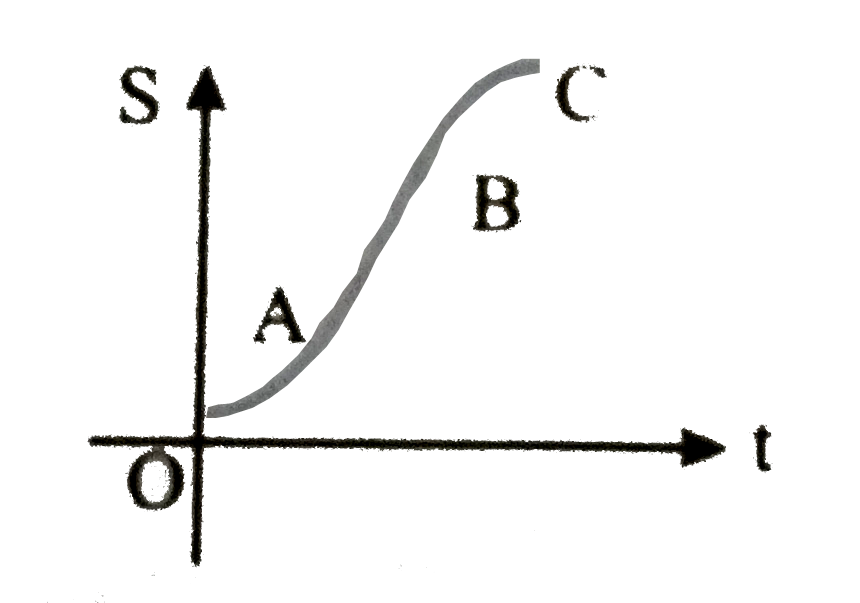
View SolutionDisplacement time graph of a particle moving in a straight line is as shown in figure. Select the correct alternative (s) :
 .
.
View Solution