Draw velocity – time graph of uniformly accelerated motion in one dimension. From the velocity – time graph of uniform accelerated motion, deduce the equations of motion in distance and time.
Step-by-Step Solution:
1. Understanding Uniformly Accelerated Motion:
- In uniformly accelerated motion, the velocity of an object changes at a constant rate. This means that the acceleration (A) is constant.
2. Drawing the Velocity-Time Graph:
- The velocity-time (V-T) graph for uniformly accelerated motion is a straight line.
- The x-axis represents time (t), and the y-axis represents velocity (v).
- At time t=0, the initial velocity is u.
- After a time t, the velocity becomes v.
3. Equation of Velocity:
- From the graph, the slope of the line represents acceleration (A).
- The relationship between final velocity (v), initial velocity (u), acceleration (A), and time (t) can be expressed as:
v=u+At
- Rearranging gives:
v−u=At(Equation 1)
4. Finding Displacement from the V-T Graph:
- The displacement (S) during the time interval can be found by calculating the area under the V-T graph.
- The area under the graph can be divided into two parts: a triangle and a rectangle.
5. Calculating Areas:
- Area 1 (Triangle):
- Base = t
- Height = v−u
- Area of triangle = 12×base×height=12×t×(v−u)
- Area 2 (Rectangle):
- Base = t
- Height = u
- Area of rectangle = u×t
6. Total Displacement:
- The total displacement (S) is the sum of the two areas:
S=Area 1+Area 2
S=12×t×(v−u)+u×t
7. Substituting for v−u:
- From Equation 1, we know v−u=At. Substituting this into the displacement equation gives:
S=12×t×(At)+u×t
S=12At2+ut
8. Final Equation of Motion:
- Thus, the equation of motion relating displacement (S), initial velocity (u), acceleration (A), and time (t) is:
S=ut+12At2
- In uniformly accelerated motion, the velocity of an object changes at a constant rate. This means that the acceleration (A) is constant.
- The velocity-time (V-T) graph for uniformly accelerated motion is a straight line.
- The x-axis represents time (t), and the y-axis represents velocity (v).
- At time t=0, the initial velocity is u.
- After a time t, the velocity becomes v.
- From the graph, the slope of the line represents acceleration (A).
- The relationship between final velocity (v), initial velocity (u), acceleration (A), and time (t) can be expressed as:
v=u+At
- Rearranging gives:
v−u=At(Equation 1)
- The displacement (S) during the time interval can be found by calculating the area under the V-T graph.
- The area under the graph can be divided into two parts: a triangle and a rectangle.
- Area 1 (Triangle):
- Base = t
- Height = v−u
- Area of triangle = 12×base×height=12×t×(v−u)
- Area 2 (Rectangle):
- Base = t
- Height = u
- Area of rectangle = u×t
- The total displacement (S) is the sum of the two areas:
S=Area 1+Area 2
S=12×t×(v−u)+u×t
- From Equation 1, we know v−u=At. Substituting this into the displacement equation gives:
S=12×t×(At)+u×t
S=12At2+ut
- Thus, the equation of motion relating displacement (S), initial velocity (u), acceleration (A), and time (t) is:
S=ut+12At2
Topper's Solved these Questions
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - LEVEL 1
75 Videos
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - LEVEL 2
65 Videos
- JEE MAIN REVISON TEST-23BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISON TEST-23EXERCISE - PHYSICS (SECTION 2)
1 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
Similar Questions
Knowledge Check
Position-time graph for motion with zero acceleration is
A B
B C
C D
D
The velocity-time graph of a linear motion is shown below . The displacement from the origin after 8 seconds is
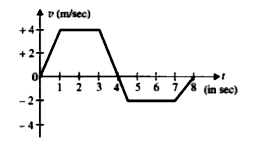 A18 mB6 mC8 mD16 m
A18 mB6 mC8 mD16 mFor a uniformly retarded motion, the velocity-time graph is :
Aa curveBa straight line parallel to the time axisCa straight line perpendicular to the time axis.Da straight line inclined to the time axis.
The velocity-time graph of a particle in straight line motion is velocity-time graph of a particle in straight line motion is shown in. The particle starts its motion from origin.
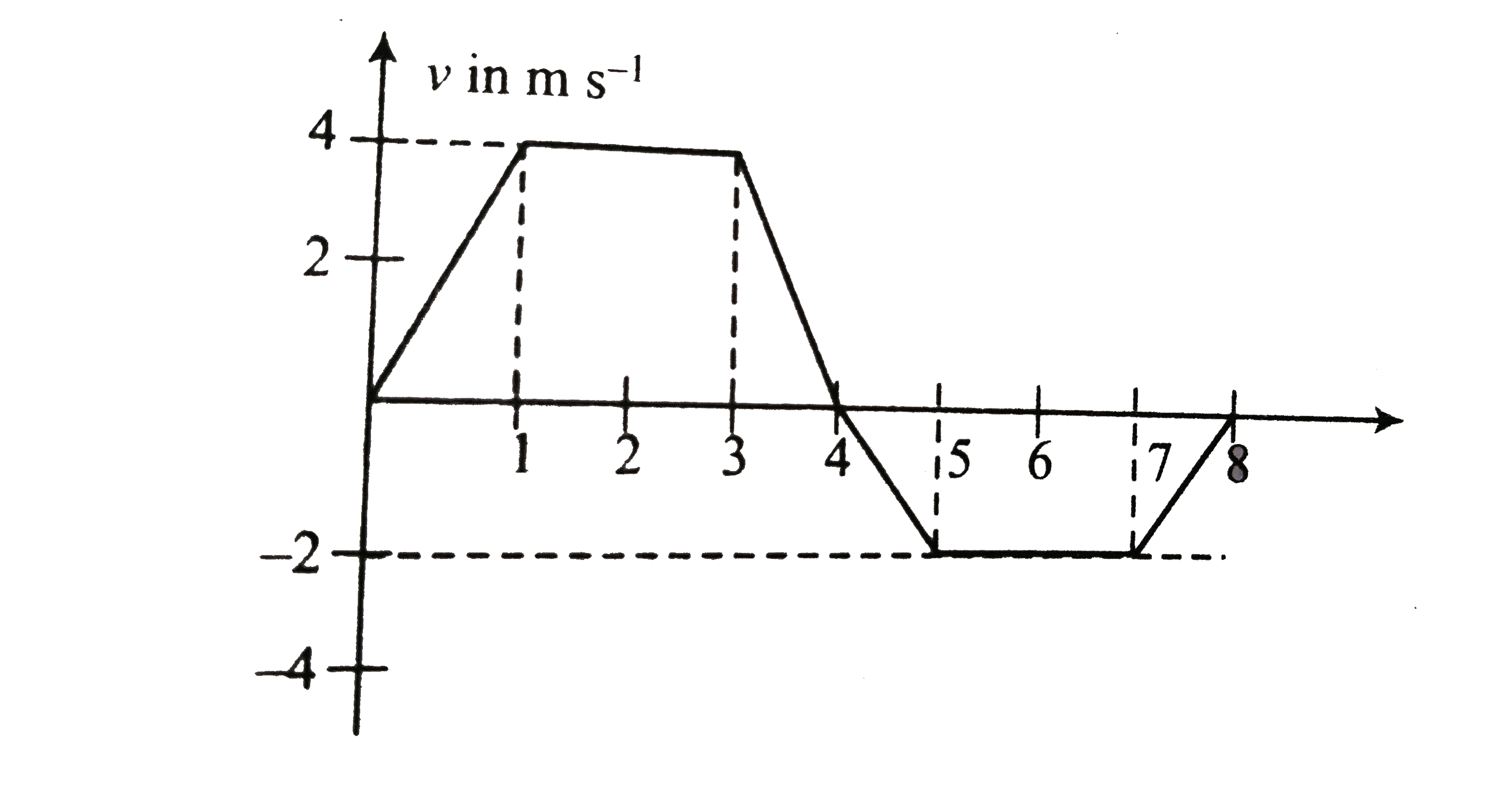 .
.
The distance of the particle from the origin after 8s is .
View SolutionDraw the velocity-time graph of an object moving with uniform negative acceleration.
View SolutionDraw a velocity-time graph for a body moving with an initial velocity u and uniform acceleration a. Use this graph to find the distance travelled by the body in time t.
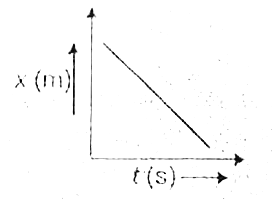
View SolutionThe position - time (x−t) graph of an object in uniform motion is shown below, the velocity of object is
View SolutionThe velocity-time graph of a linear motion is shown in figure. The displacement from the origin after 8 sec is :

View Solution
