Question

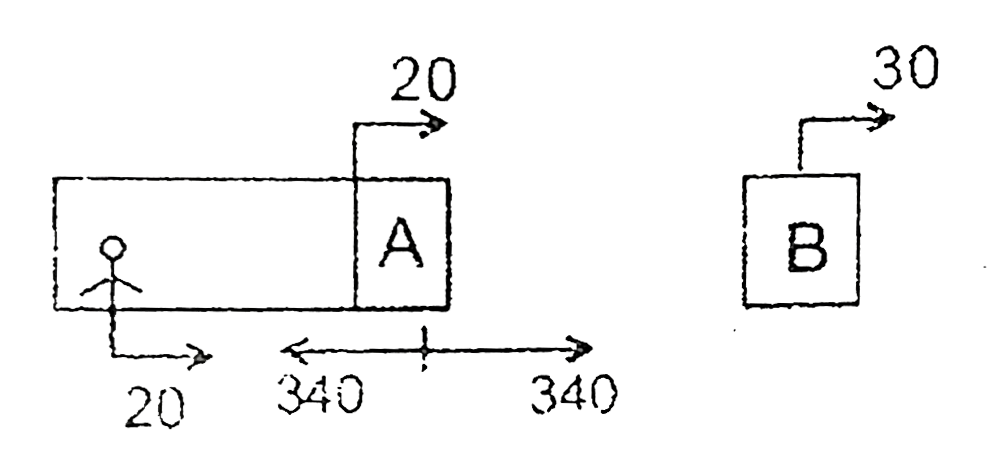
Two trains $A\text{and}B$ moving with speeds $20m/s$ and $30m/s$ respectively in the same direction on the same straight track, with $B$ ahead of $A$. The engines are at the front ends. The engine of train $A$ blows a long whistle.
Assume that the sound of the whistle is composed of components varying in frequency from $f_1=800Hz$ to $f_2=1120Hz$, as shown in the figure. The spread in the frequency (highest frequency - lowest frequency) is thus $320Hz$. The speed of sound in still air is $340m/s$.
The speed of sound of the whistle is

Options

A. (a)340 m/s for passengers in A and 310 m/s for passengers in B
B. (b)360 m/s for passengers in A and 310 m/s for passengers in B
C. (c)310 m/s for passengers in A and 360 m/s for passengers in B
D. (d)340 m/s for passengers in both the trains

Answer

B

Explanation

To solve the problem, we need to determine the speed of sound as perceived by the passengers in both trains A and B.

Step 1: Identify the given data
- Speed of train A, \( v_A = 20 \, \text{m/s} \)
- Speed of train B, \( v_B = 30 \, \text{m/s} \)
- Speed of sound in still air, \( v_s = 340 \, \text{m/s} \)
- Frequency range: \( f_1 = 800 \, \text{Hz} \) to \( f_2 = 1120 \, \text{Hz} \)
- Spread in frequency: \( \Delta f = f_2 - f_1 = 320 \, \text{Hz} \)

Step 2: Calculate the speed of sound as perceived by passenger in train A
The speed of sound relative to the passenger in train A can be calculated using the formula:
\( v_{sA} = v_s - v_A \)
Substituting the values:
\( v_{sA} = 340 \, \text{m/s} - 20 \, \text{m/s} = 320 \, \text{m/s} \)

Step 3: Calculate the speed of sound as perceived by passenger in train B
The speed of sound relative to the passenger in train B can be calculated using the formula:
\( v_{sB} = v_s - v_B \)
Substituting the values:
\( v_{sB} = 340 \, \text{m/s} - 30 \, \text{m/s} = 310 \, \text{m/s} \)

Conclusion
- The speed of sound as perceived by the passenger in train A is \( 320 \, \text{m/s} \).
- The speed of sound as perceived by the passenger in train B is \( 310 \, \text{m/s} \).