An observer moves on the same line on which two sources of sound of frequency 660Hz are present. The observer observes beat frequency of 10Hz. If speed of sound is 300m/s then speed of the observer is:
6m/s
3m/s
2.5m/s
4m/s
The correct Answer is:C
To find the speed of the observer, we can follow these steps:
Step 1: Understand the problem
We have two sound sources, both emitting sound at a frequency f=660Hz. The observer is moving along the line connecting the two sources and hears a beat frequency of 10Hz. The speed of sound in air is given as v=300m/s.
Step 2: Determine the apparent frequencies
When the observer moves towards one source (let's call it S1), the apparent frequency f1 can be calculated using the formula:
f1=(v+v0v)f
where v0 is the speed of the observer.
When the observer moves away from the other source (let's call it S2), the apparent frequency f2 is given by:
f2=(v−v0v)f
Step 3: Set up the equation for beat frequency
The beat frequency fb is the difference between the two apparent frequencies:
fb=|f1−f2|=10Hz
Substituting the expressions for f1 and f2:
∣∣∣(v+v0v)f−(v−v0v)f∣∣∣=10
Step 4: Simplify the equation
Factoring out f:
∣∣
∣∣((v+v0)−(v−v0)v)f∣∣
∣∣=10
This simplifies to:
∣∣∣2v0vf∣∣∣=10
Step 5: Substitute known values
Substituting v=300m/s and f=660Hz:
2v0300⋅660=10
Step 6: Solve for v0
Rearranging the equation gives:
2v0⋅660=10⋅300
2v0⋅660=3000
v0⋅660=1500
v0=1500660≈2.27m/s
Final Answer
The speed of the observer v0 is approximately 2.27m/s.
---
We have two sound sources, both emitting sound at a frequency f=660Hz. The observer is moving along the line connecting the two sources and hears a beat frequency of 10Hz. The speed of sound in air is given as v=300m/s.
When the observer moves towards one source (let's call it S1), the apparent frequency f1 can be calculated using the formula:
f1=(v+v0v)f
where v0 is the speed of the observer.
f2=(v−v0v)f
The beat frequency fb is the difference between the two apparent frequencies:
fb=|f1−f2|=10Hz
∣∣∣(v+v0v)f−(v−v0v)f∣∣∣=10
Factoring out f:
∣∣
∣∣((v+v0)−(v−v0)v)f∣∣
∣∣=10
This simplifies to:
∣∣∣2v0vf∣∣∣=10
Substituting v=300m/s and f=660Hz:
2v0300⋅660=10
Rearranging the equation gives:
2v0⋅660=10⋅300
2v0⋅660=3000
v0⋅660=1500
v0=1500660≈2.27m/s
The speed of the observer v0 is approximately 2.27m/s.
Topper's Solved these Questions
- JEE MAINSBook:JEE MAINS PREVIOUS YEAR ENGLISHChapter:JEE MAINSExercise:Chemistry
Explore 1 Video
- JEE MAINBook:JEE MAINS PREVIOUS YEAR ENGLISHChapter:JEE MAINExercise:All Questions
Explore 452 Videos
- JEE MAINS 2020Book:JEE MAINS PREVIOUS YEAR ENGLISHChapter:JEE MAINS 2020Exercise:PHYSICS
Explore 250 Videos
Similar Questions
A source of sound of frequency 500 Hz is moving towards an observer with velocity 30 m/s . The speed of sound is 330 m/s . the frequency heard by the observer will be
View SolutionA source is moving with constant speed υs=20m/s towards a stationary observer due east of the source. Wind is blowing at the speed of 20m/s at 60∘ north of east. The source has frequency 500HZ. Speed of sound =300m/s. The frequency resgistered by the observer is approximately
View SolutionTo an observer, the pitch of a stationary source of sound appears to be reduced by 20%. If the speed of sound is 340m/s then speed and direction of the observer is
View SolutionIf source and observer both are relatively at rest and if speed of sound is increased then frequency heard by observer will
View SolutionA source of sound is travelling towards a stationary observer. The frequency of sound heard by the observer is 25% more that the actual frequency. If the speed of sound is v, that of the source is
View SolutionWhen a source moves away from a stationary observer, the frequency is 67 times the original frequency. Given: speed of sound =330ms . The speed of the source is
View SolutionFor a certain organ pipe three successive resonance frequencies are observed at 425Hz, 595 Hz and 765Hz respectively. If the speed of sound air is 340m/s, then the length of the pipe is
View Solution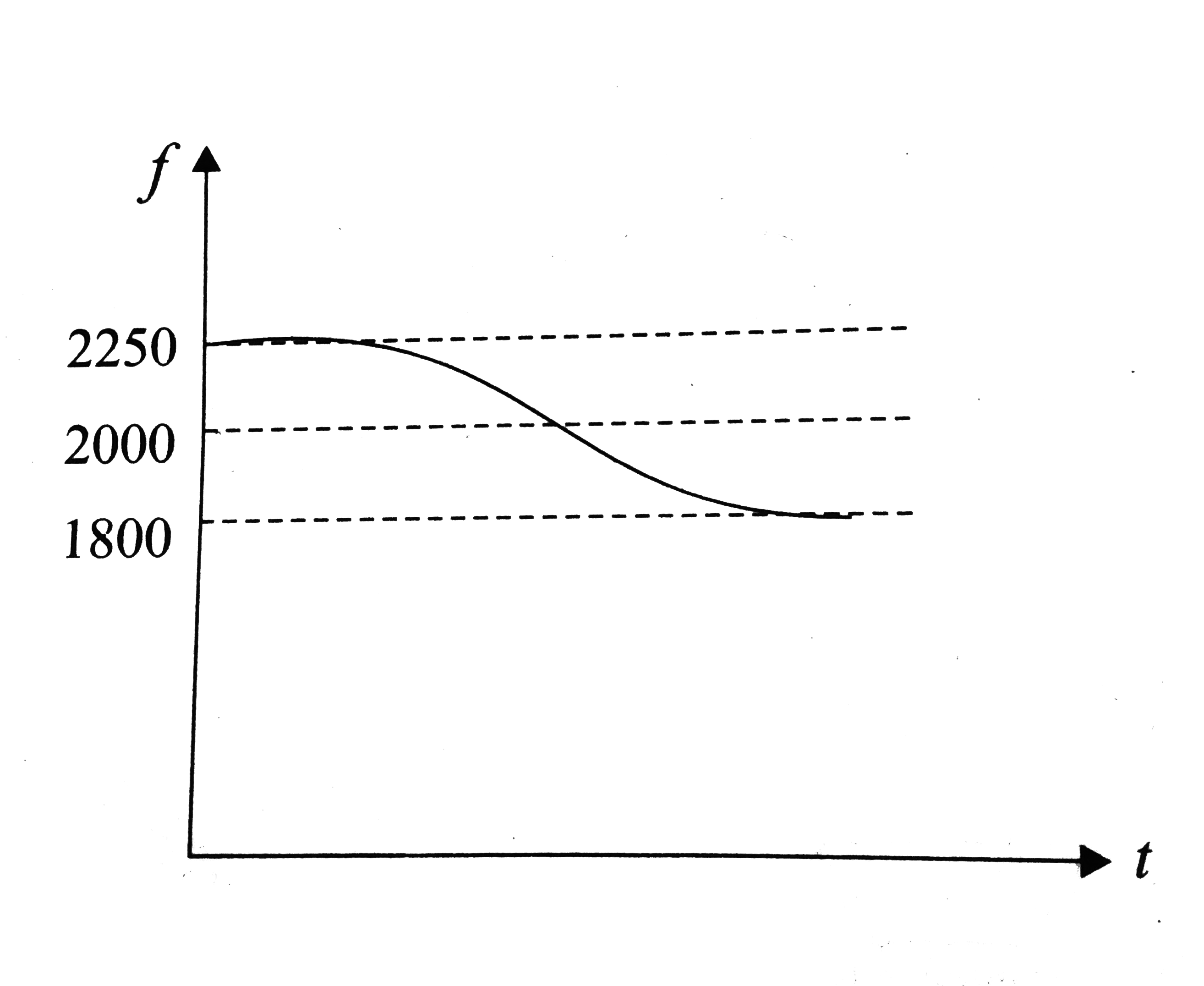
A statinary observer receives a sound of frequency 2000 Hz. The variation of apparent frequency and time is shown. Find the speed of source, if velocity of sound is 300ms
View SolutionTwo tuning forks with natural frequencies of 340Hz each move relative to a stationary observer. One fork moves away form the observer, while the other moves towards him at the same speed. The observer hears beats of frequency 3Hz. Find the speed of the tuning fork.
View SolutionA source and an observer are situated on two perpendicular tracks as shown in the figure the observer is at rest and source is moving with a speed 50m/s the source emits sound waves of frequency 90Hz which travel in the medium with velocity 200m/s the frequency of sound heard by observer when the source crosses the origin is

View Solution

