A drop of liquid of density is floating half-immersed in a liquid of density . If is the surface tension the diameter of the drop of the liquid is
the speed of the particle when it returns to its equilibrium position is
the time at which the particle passes through the equilibrium position for the first time is
the time at which the maximum compression of the spring occurs is
the time at which the particle passes through the equilibrium position for the second time is the time at which the maximum compression of the spring occurs is
The correct Answer is:AD
(suppose is the time of collision)
Now the particle returns to equilibrium position at time ,i.e., with same mechanical energy, i.e., its speed will be Let t be the time at which the particle passes through the equilibrium position for the second time.
Time at which maximum compression of spring occurs =
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:6-previous year question
Explore 56 Videos
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:JEE Advanced (Archive) (True/False Type)
Explore 3 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBook:VMC MODULES ENGLISHChapter:SYSTEM OF A PARTICLES & ROTATIONAL MOTIONExercise:IN-CHAPTER EXERCISE F
Explore 10 Videos
Similar Questions
A solid of density D is floating in a liquid of density d. If υ is the volume of solid submerged in the liquid and V is the total volume of the solid, then υ/V equal to
View SolutionAn object of mass m is floating in a liquid of density σ. If the object is made up of density ρ, then appare weight of the object in the liquid is
View Solution
Knowledge Check
The pressure inside a liquid of density ρ at a depth h is :
AhρgBhρgChρgDhρ
A sphere of density ρ is half submerged in a liquid of density σ and surface tension T. The sphere remains in equilibrium. Find radius of the sphere (assume the force due to surface tension acts tangentially to surface of sphere)
View SolutionAn object of w and density ρ is submerged in liquid of density σ, its apparent weight will be
View SolutionA small ball of density ρ is immersed in a liquid of density σ(>ρ) to a depth h and released. The height above the surface of water up to which the ball will jump is
View Solution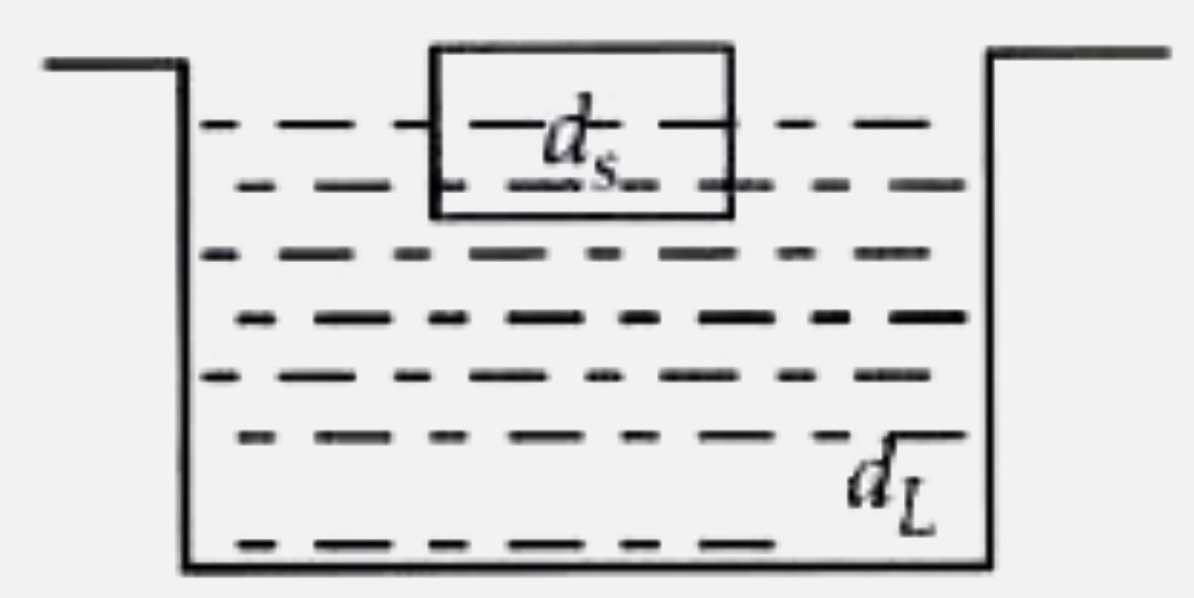
The figure above shows a solid of density dS floating in a liquid of density dL.
What is the apparent weight of the floating body?
View SolutionA body of density ρ sinks in a liquid of density ρL.The densities ρ and ρL are related as:
View SolutionA block of density ρ floats in a liquid with its one third volume immersed. The density of the liquid is
View SolutionA body of density ρ is immersed in a liquid of density ρL.State condition when the body will (i) float (ii) sink in liquid.
View Solution

