If a spring of stiffness 'k' is cut into two parts 'A' and 'B' of length lA:lB=2:3, then the stiffness of spring 'A' is given by
52k
3k5
2k5
k
The correct Answer is:A
To find the stiffness of spring A after cutting a spring of stiffness k into two parts A and B with a length ratio of lA:lB=2:3, we can follow these steps:
1. Understand the Length Ratio:
Given the ratio lA:lB=2:3, we can express the lengths of parts A and B in terms of a common length. Let the total length of the spring be L. Then:
lA=25LandlB=35L
2. Relationship Between Stiffness and Length:
The stiffness k of a spring is inversely proportional to its length. This means:
k∝1l
Therefore, if we denote the stiffness of spring A as kA and the stiffness of spring B as kB, we can write:
kA⋅lA=k⋅L
3. Express Stiffness of Spring A:
From the relationship above, we can rearrange to find kA:
kA=k⋅LlA
4. Substituting the Length of Spring A:
Now substitute lA=25L into the equation:
kA=k⋅L25L
5. Simplifying the Expression:
The L cancels out:
kA=k25=k⋅52
6. Final Result:
Thus, the stiffness of spring A is:
kA=52k
Conclusion:
The stiffness of spring A after cutting the original spring is 52k.
Given the ratio lA:lB=2:3, we can express the lengths of parts A and B in terms of a common length. Let the total length of the spring be L. Then:
lA=25LandlB=35L
The stiffness k of a spring is inversely proportional to its length. This means:
k∝1l
Therefore, if we denote the stiffness of spring A as kA and the stiffness of spring B as kB, we can write:
kA⋅lA=k⋅L
From the relationship above, we can rearrange to find kA:
kA=k⋅LlA
Now substitute lA=25L into the equation:
kA=k⋅L25L
The L cancels out:
kA=k25=k⋅52
Thus, the stiffness of spring A is:
kA=52k
The stiffness of spring A after cutting the original spring is 52k.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL (2)
40 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)
3 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
Similar Questions
A spring of length 'l' has spring constant 'k' is cut into two parts of length l1 and l2. If their respective spring constahnt are K1 and k2, then K1K2 is:
View SolutionIf a spring of force constant 'k' is cut into two parts, such that one part is thrice in length of the other part. Then the force constant of each part are
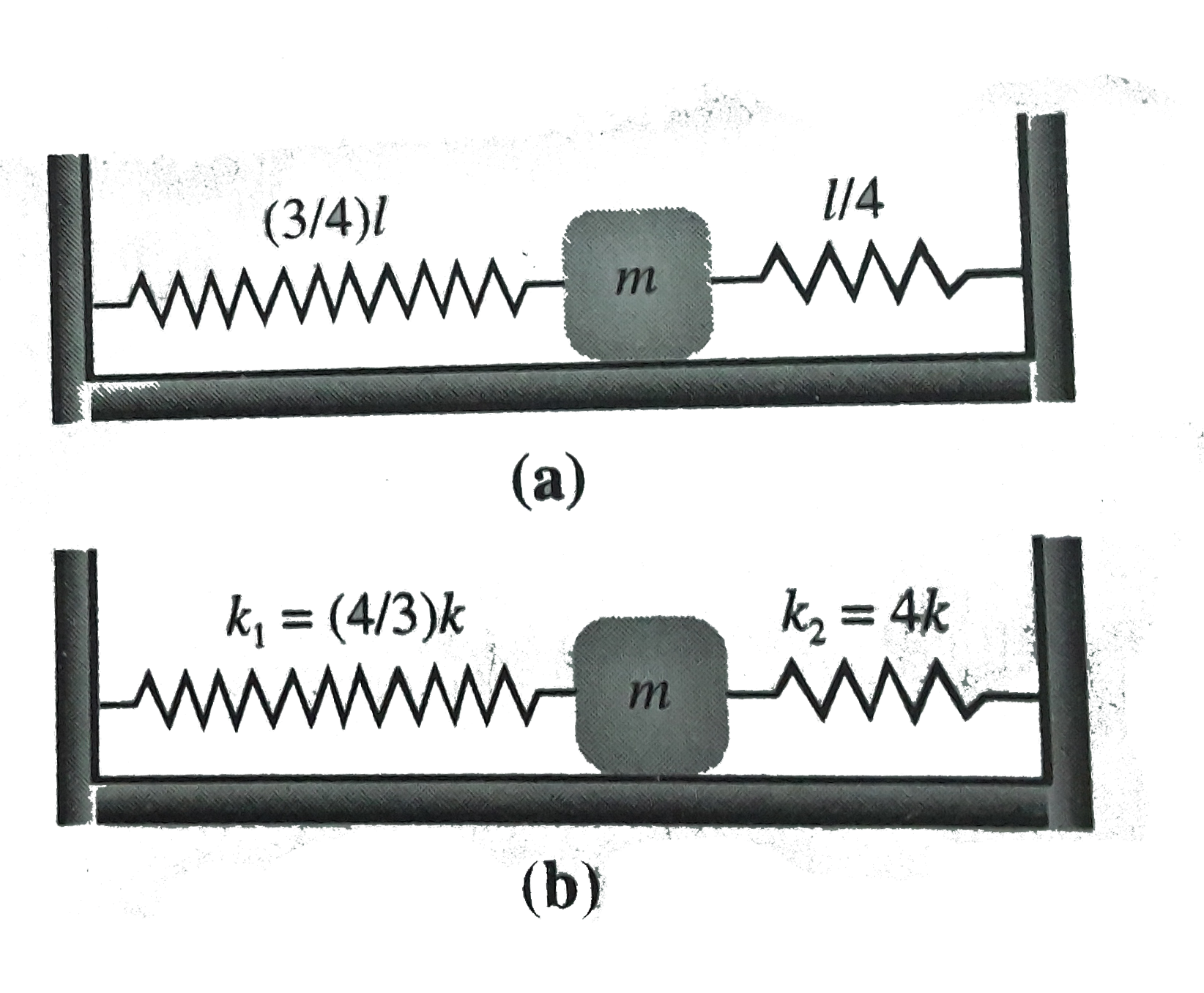
View SolutionA spring of stiffness constant k and natural length l is cut into two parts of length 3l/4andl/4, respectively, and an arrangement is made as shown in figure . If the mass is slightly displaced , find the time period of oscillation.
View SolutionTwo identicle particles A and B, each of mass m, are interconnected by a spring of stiffness k. If particle B experiences a forec F and the elongation of the spring is x, the acceleration of particle B relative to particle A is equal to

View SolutionA spring of certain length and having spring constant k is cut into two pieces of length in a ratio 1:2. The spring constants of the two pieces are in a ratio :
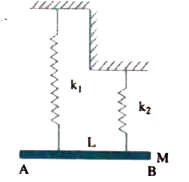
View SolutionWhen a mass M hangs from a spring of length l, it stretches the spring by a distance x. Now the spring is cut in two parts of length l/3 and 2l/3, and the two springs thus formed are connected to a straight rod of mass M which is horizontal in the configuration shown in figure. Find the stretch in each of the spring.
View SolutionA disc of mass m hanged by a string is attached at P and a spring of stiffness k is attached at Q. Find the frequency of small angular oscillation of the disc if the string does not slide over the pulley. Assume l0=Ml of the dise about O.

View SolutionA uniform spring whose unstressed length is l has a force constant k. The spring is cut into two pieces of unstressed lengths l1 and l2 where l1=nl2 where n being on integer. Now a mass m is made to oscillate with first spring. The time period of its oscillation would be
View SolutionAssertion A spring of force constatn k is cut in to two piece having lengths in the ratio 1:2 The force constant of series combination of the two parts is 3k2
The spring connected in series are represented by k=k1+k2
View SolutionTime period of a spring mass system is T.If this spring is cut into two parts whose lengths are in ratio 1:3 and the same mass is attached to the longer part, the new time period will be
View Solution
