A uniform spring whose unstressed length is l has a force constant k. The spring is cut into two pieces of unstressed lengths l1 and l2 where l1=nl2 where n being on integer. Now a mass m is made to oscillate with first spring. The time period of its oscillation would be
T=2π√mnk(n+1)
T=2π√mk(n+1)
T=2π√mk
T=2π√m(n+1)nk
The correct Answer is:A
To solve the problem step by step, we will analyze the situation involving the spring and the mass oscillating on it.
1. Understanding the Problem:
- We have a uniform spring with an unstressed length l and a spring constant k.
- The spring is cut into two pieces with lengths l1 and l2, where l1=nl2 (with n being an integer).
- We need to find the time period of oscillation when a mass m is attached to the first spring l1.
2. Finding the Lengths of the Springs:
- Since l1+l2=l and l1=nl2, we can substitute to find l2:
nl2+l2=l⟹(n+1)l2=l⟹l2=ln+1
- Now, substituting l2 back to find l1:
l1=nl2=n(ln+1)=nln+1
3. Finding the Spring Constants:
- The spring constant of a spring is inversely proportional to its length. The product of the length and spring constant remains constant for a uniform spring.
- For the original spring:
k⋅l=keffective⋅l1⟹keffective=k⋅ll1
- For the first spring l1:
keffective=k⋅lnln+1=(n+1)kn
4. Calculating the Time Period:
- The time period T of oscillation for a mass m attached to a spring is given by:
T=2π√mkeffective
- Substituting keffective:
T=2π√m(n+1)kn=2π√mn(n+1)k
5. Final Result:
- The time period of the oscillation of the mass m with the first spring l1 is:
T=2π√mn(n+1)k
- We have a uniform spring with an unstressed length l and a spring constant k.
- The spring is cut into two pieces with lengths l1 and l2, where l1=nl2 (with n being an integer).
- We need to find the time period of oscillation when a mass m is attached to the first spring l1.
- Since l1+l2=l and l1=nl2, we can substitute to find l2:
nl2+l2=l⟹(n+1)l2=l⟹l2=ln+1
- Now, substituting l2 back to find l1:
l1=nl2=n(ln+1)=nln+1
- The spring constant of a spring is inversely proportional to its length. The product of the length and spring constant remains constant for a uniform spring.
- For the original spring:
k⋅l=keffective⋅l1⟹keffective=k⋅ll1
- For the first spring l1:
keffective=k⋅lnln+1=(n+1)kn
- The time period T of oscillation for a mass m attached to a spring is given by:
T=2π√mkeffective
- Substituting keffective:
T=2π√m(n+1)kn=2π√mn(n+1)k
- The time period of the oscillation of the mass m with the first spring l1 is:
T=2π√mn(n+1)k
Similar Questions
A uniform spring whose unstretched length is l has a force constant k. the spring is cut into two pieces of unstretched lengths l1 and l2, where l1=nl2 and n is an integer. What are the corresponding force constant k1 and k2 in terms of n and k?
View SolutionA spring whose instretched length is l has a force constant k. The spring is cut into two pieces of unstretched lengths l1 and l2 where, l1=nl2 and n is an integer. The ratio k1/k2 of the corresponding force constant, k1 and k2 will be :
View SolutionA uniform spring whose unstretched length is l has a force constant k. the spring is cut into two pieces of unstretched lengths l1 and l2, where l1=nl2 and n is an integer. What are the corresponding force constant k1 and k2 in terms of n and k? what is the ratio k1/k2
View SolutionA spring of length 'l' has spring constant 'k' is cut into two parts of length l1 and l2. If their respective spring constahnt are K1 and k2, then K1K2 is:
View SolutionA spring of force constant 'k' is cut into four equal parts one part is attached with a mass m. The time period of oscillation will be
View SolutionA uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is

View SolutionA spring of stiffness constant k and natural length l is cut into two parts of length 3l/4andl/4, respectively, and an arrangement is made as shown in figure . If the mass is slightly displaced , find the time period of oscillation.
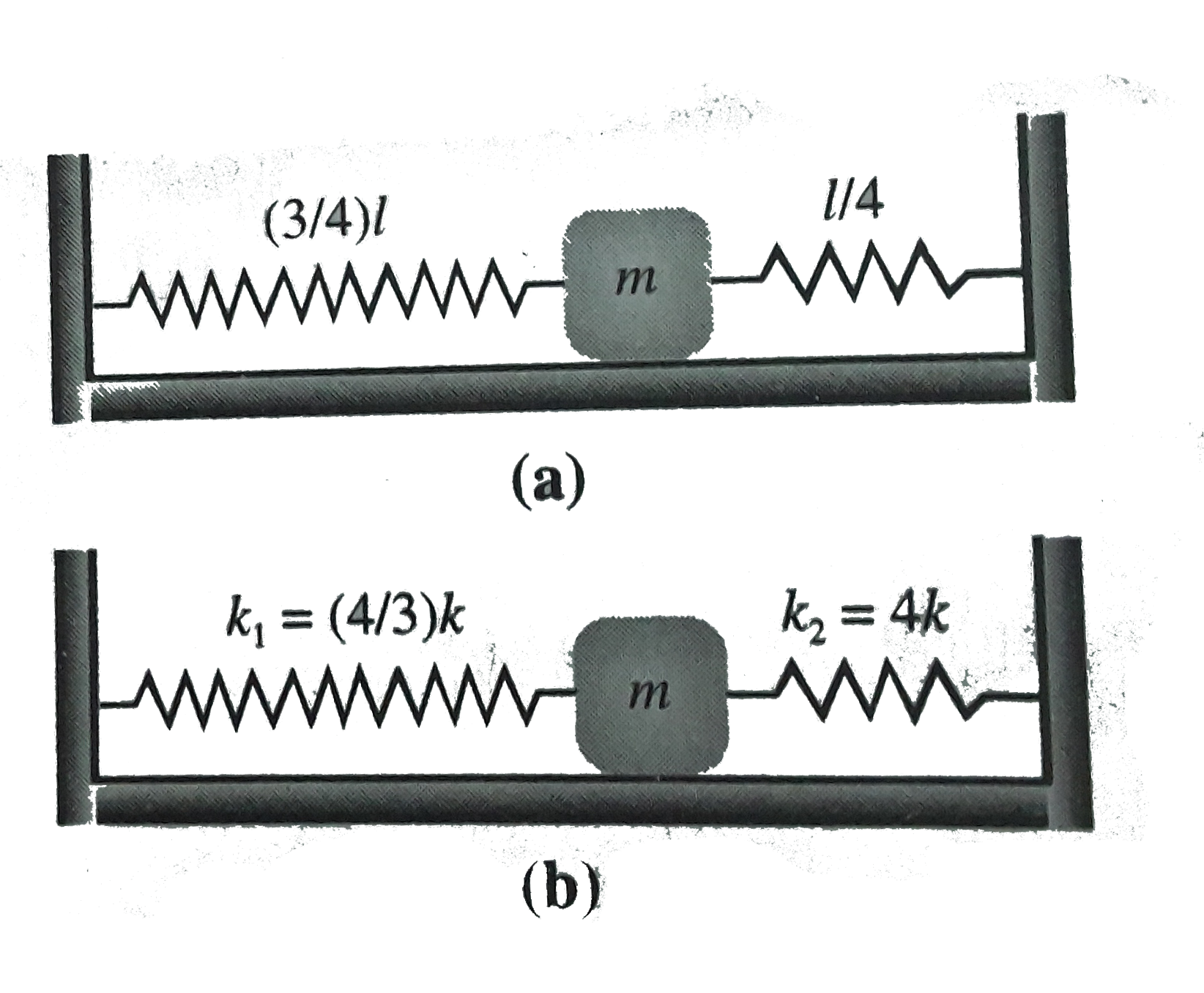
View SolutionA uniform spring has a centain block suspended from it and its period for vertical oscillation is T1. The spring is now cut into two parts of lengths 13rdand23rd of original length and these springs are connected to the same block as shown in the figure. If time period of oscillation now is T2 then T1/T2.

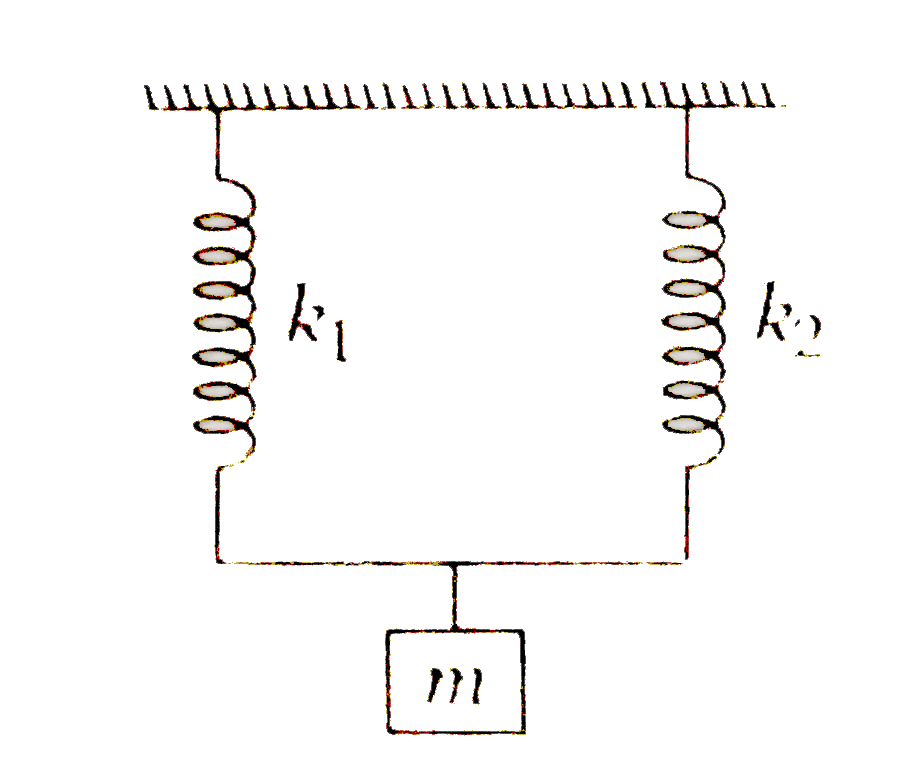
View SolutionThe spring constants of two springs of same length are k1 and k2 as shown in figure. If an object of mass m is suspended and set in vibration , the period will be
View SolutionA block of mass m, when attached to a uniform ideal apring with force constant k and free length L executes SHM. The spring is then cut in two pieces, one with free length n L and other with free length (1−n)L. The block is also divided in the same fraction. The smaller part of the block attached to longer part of the spring executes SHM with frequency f1 . The bigger part of the block attached to smaller part of the spring executes SHM with frequency f2. The ratio f1/f2 is
View Solution