If a spring of stiffness 'k' is cut into two parts 'A' and 'B' of length lA:lB=2:3, then the stiffness of spring 'A' is given by
52k
3k5
2k5
k
The correct Answer is:A
To find the stiffness of spring A after cutting the original spring into two parts A and B in the ratio of their lengths lA:lB=2:3, we can follow these steps:
1. Define the Total Length of the Spring:
Let the total length of the original spring be L.
2. Determine the Lengths of Springs A and B:
Given the ratio lA:lB=2:3, we can express the lengths of A and B in terms of L:
lA=25LandlB=35L
3. Use the Relationship Between Stiffness and Length:
The product of stiffness k and length L is a constant. Therefore, we can write:
k⋅L=kA⋅lA=kB⋅lB
where kA and kB are the stiffnesses of springs A and B, respectively.
4. Set Up the Equation for Spring A:
From the relationship, we can express the stiffness of spring A:
k⋅L=kA⋅(25L)
5. Solve for kA:
Rearranging the equation gives:
kA=k⋅L25L=k⋅L⋅52L=52k
6. Conclusion:
The stiffness of spring A is:
kA=52k
Let the total length of the original spring be L.
Given the ratio lA:lB=2:3, we can express the lengths of A and B in terms of L:
lA=25LandlB=35L
The product of stiffness k and length L is a constant. Therefore, we can write:
k⋅L=kA⋅lA=kB⋅lB
where kA and kB are the stiffnesses of springs A and B, respectively.
From the relationship, we can express the stiffness of spring A:
k⋅L=kA⋅(25L)
Rearranging the equation gives:
kA=k⋅L25L=k⋅L⋅52L=52k
The stiffness of spring A is:
kA=52k
Topper's Solved these Questions
- WORK, ENERGY AND POWERBook:PRADEEPChapter:WORK, ENERGY AND POWERExercise:Comprehension
Explore 9 Videos
- WORK, ENERGY AND POWERBook:PRADEEPChapter:WORK, ENERGY AND POWERExercise:Integer Type Questions
Explore 9 Videos
- WORK, ENERGY AND POWERBook:PRADEEPChapter:WORK, ENERGY AND POWERExercise:NCERT( Multiple choide questions-1)
Explore 21 Videos
- THERMODYNAMICSBook:PRADEEPChapter:THERMODYNAMICSExercise:Assertion- Reason Type Questions
Explore 19 Videos
Similar Questions
Knowledge Check
A spring of length 'l' has spring constant 'k' is cut into two parts of length l1 and l2. If their respective spring constahnt are K1 and k2, then K1K2 is:
Al2l1B2l2l1Cl1l2DNoneA spring has length'l' and spring constant 'k'. It is cut into two pieces of lengths l1andl2 such that l1=nl2. The force constant of the spring of length l1 is
Ak(l+n)BkCk(n+1)Dk(n+l)nA spring of constant K is cut into two parts of length in the ratio 2:3 . The spring constant of large spring is
A53KB23KCkD35k
If a spring of force constant 'k' is cut into two parts, such that one part is thrice in length of the other part. Then the force constant of each part are
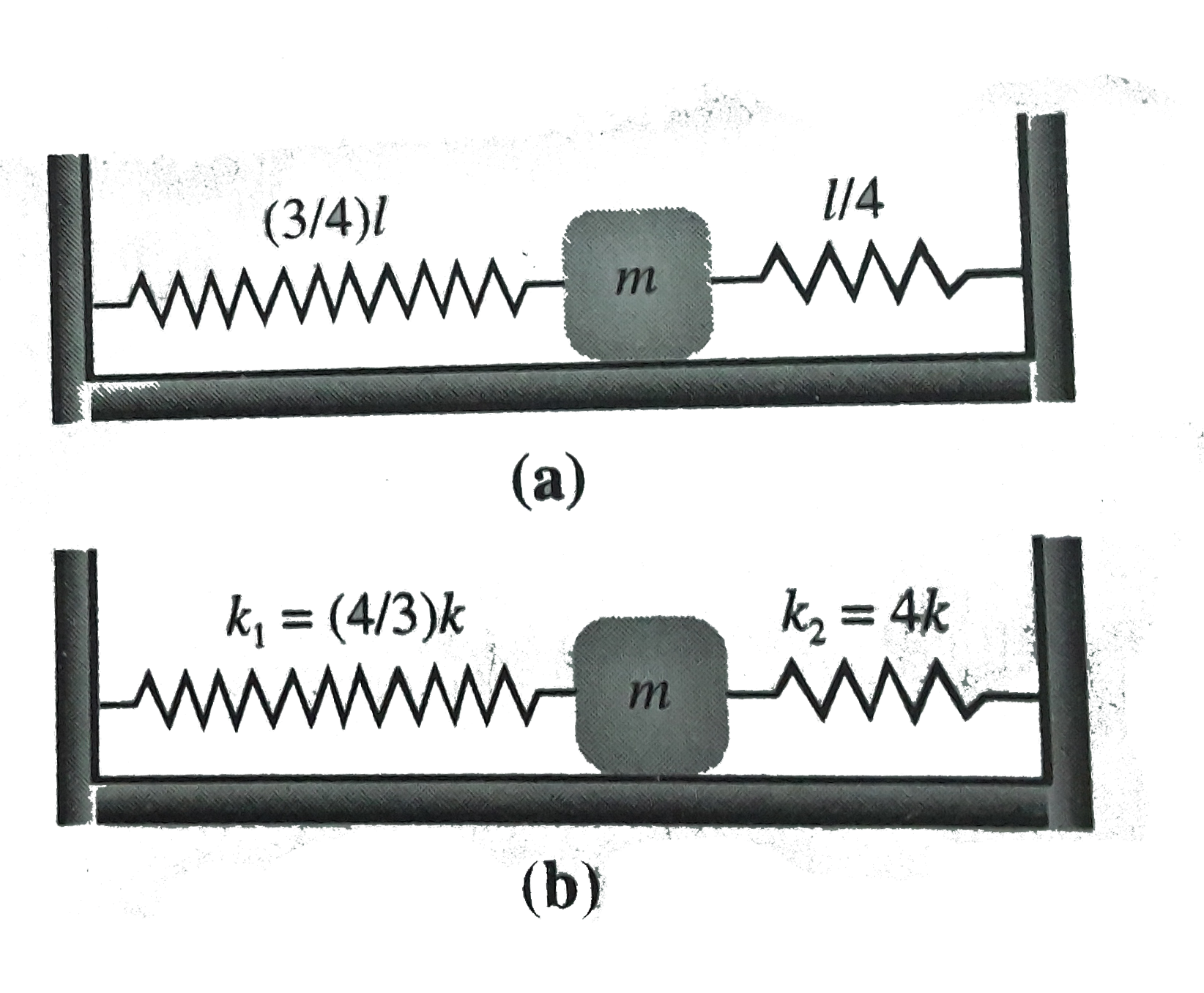
View SolutionA spring of stiffness constant k and natural length l is cut into two parts of length 3l/4andl/4, respectively, and an arrangement is made as shown in figure . If the mass is slightly displaced , find the time period of oscillation.
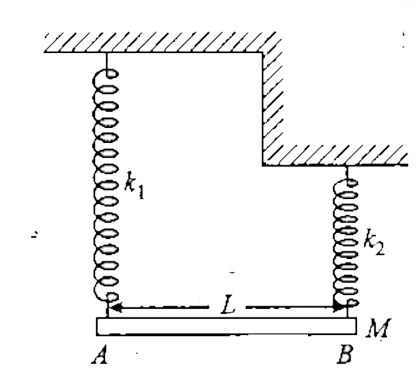
View SolutionWhen a mass M hangs from a spring of length l, it stretches the spring by a distance x. Now the spring is cut in two parts of lengths l/3 and 2l/3, and the two springs thus formed are connected to a straight rod of mass M which is horizontal in the configuration shown in figure-2.111. Find the stretch in each of the spring.
View SolutionTwo identicle particles A and B, each of mass m, are interconnected by a spring of stiffness k. If particle B experiences a forec F and the elongation of the spring is x, the acceleration of particle B relative to particle A is equal to

View SolutionA spring of certain length and having spring constant k is cut into two pieces of length in a ratio 1:2. The spring constants of the two pieces are in a ratio :
View Solution

