On a friction surface a block a mass moving at speed collides elastic with another block of same mass which is initially at rest . After collision the first block moves at an angle to its initial direction and has a speed . The second block's speed after the collision is
The correct Answer is:B
Refer to figure. As the collision is perfectly elastic hence the laws of conservation of linear momentum and kinetic energy are obeyed.
Accordin to law of conservation of kinetic energy
Total KE before collision total KE after collision
or or
or
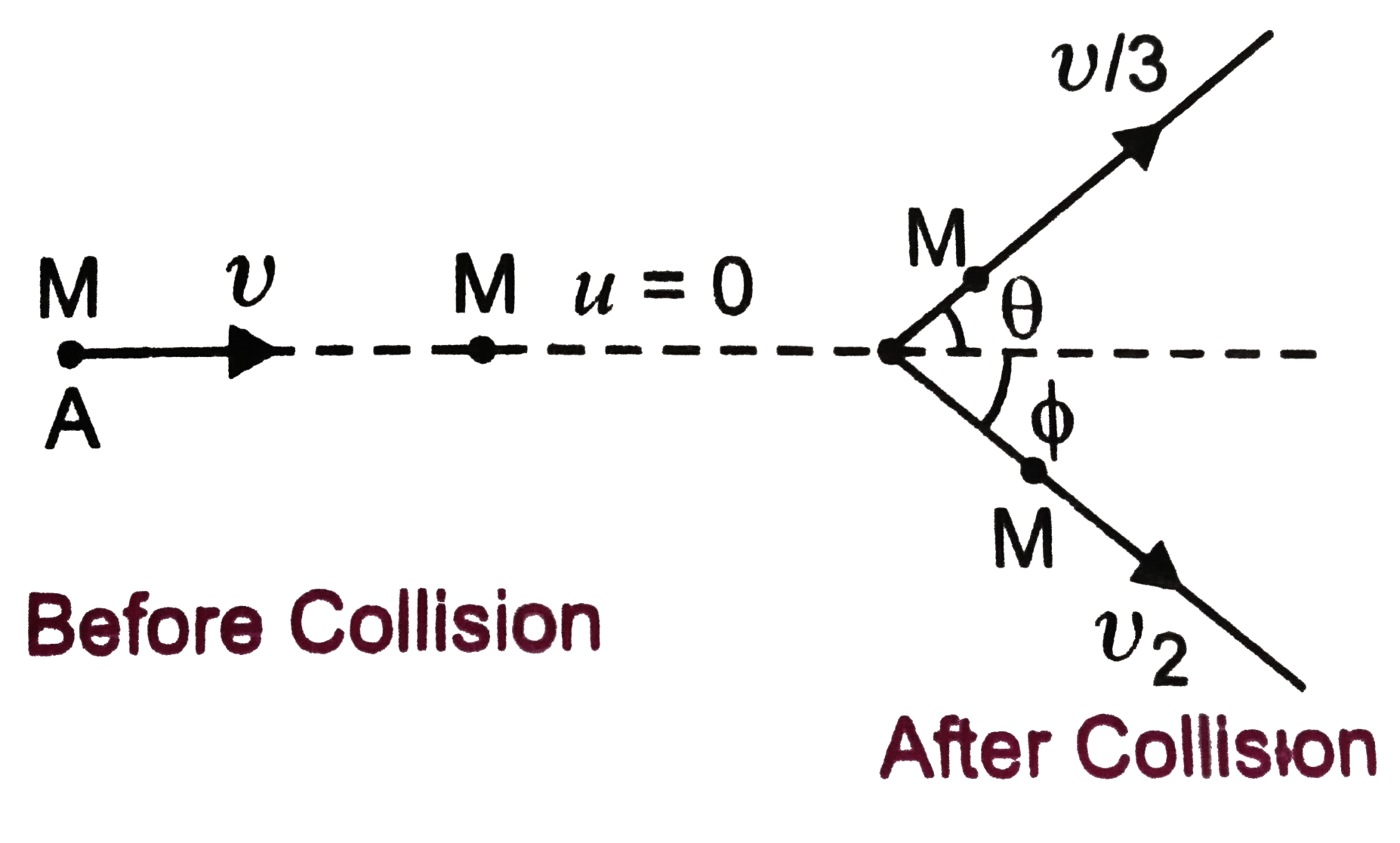
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Comprehension
9 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Integer Type Questions
9 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - NCERT( Multiple choide questions-1)
21 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions
19 Videos
Similar Questions
On a frictionless surface,a block of mass M moving at speed v collides elastically with another block of same mass M which is initially at rest.After collision the first block moves at an angle θ to its initial direction and has a speed v3 .The second block's speed after the collision is ?
View SolutionA body of mass m moving with velocity v collides head-on elastically with another body of mass 2m which is initially at rest. The ratio of K. E. of mass m before and after the collision will be
View Solution
Knowledge Check
On a frictionless surface, a block of mass M moving at speed v collides elastically with another block of same mass M which is initially at rest. After collision the first block moves at an angle θ to its initial direction and has a speed v3. The second block.s speed after the collision is
A3√2vB√32vC2√23vD34vA block of mass 'm' moving on a frictionless surface at speed 'v' collides elastically with a block of same mass, initially at rest. Now the first block moves at an angle θ with its initial direction and has speed v1 . The speed of the second block after collision is
A√v21−v2B√v2−v21C√v2+v21D√v−v1A ball A of mass 1kg , moving with a speed of 12m/s , collides obliquely and elasticity with another ball B which was initially at rest. Ball A then moves off at the right angle to its initial direction with a speed of 5m/s. The momentum of ball B after the collision is
A5kgm/sB11kgm/sC13kgm/sD17kgm/
A block of mass m moving at speed υ collides wilth another block of mass 2 m at rest. The lighter block comes to rest after the collision. Find the coefficient of restitution.
View SolutionA ball of mass m moving at a speed v collides with another ball of mass 3m at rest. The lighter block comes to rest after collisoin. The coefficient of restitution is
View SolutionA particle of mass m moving with speed V collides eleastically with another particle of mass 2mFind speed of smaller mass after head on collision
View SolutionA block of mass m moving with speed v , collides head on with another block of mass 2m at rest .
If coefficient of restitution is 12 then what is velocity of first block after the impact ?
View SolutionA block of mass 1kg moving with a speed of 4ms−1, collides with another block of mass 2kg which is at rest. The lighter block comes to rest after collision. The loss in KE of the system is
View Solution
