A block of mass 1kg moving with a speed of 4ms−1, collides with another block of mass 2kg which is at rest. The lighter block comes to rest after collision. The loss in KE of the system is
8 J
4×10−7J
4 J
0 J
The correct Answer is:C
To solve the problem step-by-step, we will calculate the loss in kinetic energy (KE) of the system after the collision.
Step 1: Calculate the initial kinetic energy of the system
The initial kinetic energy (KE_initial) of the system can be calculated using the formula:
KE=12mv2
For the 1 kg block moving at 4 m/s:
KEinitial=12×1kg×(4m/s)2=12×1×16=8J
The 2 kg block is at rest, so its kinetic energy is:
KE2kg=12×2kg×(0m/s)2=0J
Thus, the total initial kinetic energy of the system is:
KEinitial_total=KEinitial+KE2kg=8J+0J=8J
Step 2: Determine the final kinetic energy of the system
After the collision, the 1 kg block comes to rest, and we need to find the velocity of the 2 kg block. We can use the conservation of momentum:
Initial momentum=Final momentum
The initial momentum is:
pinitial=(1kg×4m/s)+(2kg×0)=4kg m/s
Let v2 be the final velocity of the 2 kg block. The final momentum is:
pfinal=(1kg×0)+(2kg×v2)=2v2
Setting the initial momentum equal to the final momentum gives:
4=2v2⟹v2=2m/s
Now we can calculate the final kinetic energy of the system:
KEfinal=KE1kg+KE2kg
The kinetic energy of the 1 kg block is:
KE1kg=12×1×(0)2=0J
The kinetic energy of the 2 kg block is:
KE2kg=12×2×(2)2=12×2×4=4J
Thus, the total final kinetic energy of the system is:
KEfinal_total=0J+4J=4J
Step 3: Calculate the loss in kinetic energy
The loss in kinetic energy (ΔKE) is given by:
ΔKE=KEinitial_total−KEfinal_total
Substituting the values we found:
ΔKE=8J−4J=4J
Final Answer
The loss in kinetic energy of the system is 4 J.
---
The initial kinetic energy (KE_initial) of the system can be calculated using the formula:
KE=12mv2
For the 1 kg block moving at 4 m/s:
KEinitial=12×1kg×(4m/s)2=12×1×16=8J
The 2 kg block is at rest, so its kinetic energy is:
KE2kg=12×2kg×(0m/s)2=0J
Thus, the total initial kinetic energy of the system is:
KEinitial_total=KEinitial+KE2kg=8J+0J=8J
After the collision, the 1 kg block comes to rest, and we need to find the velocity of the 2 kg block. We can use the conservation of momentum:
Initial momentum=Final momentum
The initial momentum is:
pinitial=(1kg×4m/s)+(2kg×0)=4kg m/s
Let v2 be the final velocity of the 2 kg block. The final momentum is:
pfinal=(1kg×0)+(2kg×v2)=2v2
Setting the initial momentum equal to the final momentum gives:
4=2v2⟹v2=2m/s
Now we can calculate the final kinetic energy of the system:
KEfinal=KE1kg+KE2kg
The kinetic energy of the 1 kg block is:
KE1kg=12×1×(0)2=0J
The kinetic energy of the 2 kg block is:
KE2kg=12×2×(2)2=12×2×4=4J
Thus, the total final kinetic energy of the system is:
KEfinal_total=0J+4J=4J
The loss in kinetic energy (ΔKE) is given by:
ΔKE=KEinitial_total−KEfinal_total
Substituting the values we found:
ΔKE=8J−4J=4J
The loss in kinetic energy of the system is 4 J.
Topper's Solved these Questions
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level- II (C.W)
Explore 68 Videos
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level- III (C.W)
Explore 50 Videos
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:C.U.Q-Key
Explore 75 Videos
- WORK , ENERGY & POWER Book:NARAYNAChapter:WORK , ENERGY & POWER Exercise:EXERCISE IV
Explore 43 Videos
Similar Questions
A block of mass m moving at speed υ collides wilth another block of mass 2 m at rest. The lighter block comes to rest after the collision. Find the coefficient of restitution.
View SolutionA spring-block system is resting on a frictionless floor as shown in the figure. The spring constant is 2.0Nm−1 and the mass of the block is 2.0 kg. Ignore the mass of the spring. Initially the spring is in an unstretched condition. Another block of mass 1.0 kg moving with a speed of 2.0ms−1 collides elastically with the first block. The collision is such that the 2.0 kg block does not hit the wall. The distance, in metres, between the two blocks when the spring returns to its unstretched position for the first time after the collision is
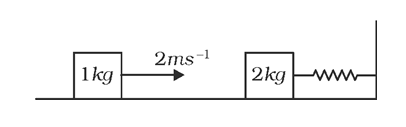
View Solution
Knowledge Check
A block of mass 1kg moving with a speed of 4ms−1, collides with another block of mass 2kg which is at rest. If the lighter block comes to rest after collision, then the speed of the heavier body is
A2ms−1B1ms−1C1.5ms−1D0.5ms−1A ball of mass m moving at a speed v collides with another ball of mass 3m at rest. The lighter block comes to rest after collisoin. The coefficient of restitution is
A(a) 12B(b) 23C(c) 14D(d) None of theseA body of mass 4kg moving with velocity 12m/s collides with another body of mass 6kg at rest. If two bodies stick together after collision , then the loss of kinetic energy of system is
AzeroB288JC172.8JD144J
A spring-block system is resting on a frictionless floor as shown in the figure. The spring constant is 2.0 Nm–1 and the mass of the block is 2.0 kg. Ignore the mass of the spring. Initially the spring is in an unstretched condition. Another block of mass 1.0 kg moving with a speed of 2.0 m s–1 collides elastically with the first block. The collision is such that the 2.0 kg block does not hit the wall. The distance, in metres, between the two blocks when the spring returns to its unstretched position for the first time after the collision is _________.

View SolutionA body of mass 5 kg moving with a velocity 10 m/s collides with another body of the mass 20 kg at rest, and comes to rest. The velocity of the second body due to collision is
View SolutionA body of mass 5 kg moving with a velocity 10 m/s collides with another body of the mass 20 kg at, rest and comes to rest. The velocity of the second body due to collision is
View SolutionA moving block having mass m , collides with another stationary block having mass 4m. The lighter block comes to rest after collision. When the initial velocity of the block is v, then the value of coefficient of restitution (e) will be
View SolutionA moving block having mass m, collides with another stationary block having mass 4m. The lighter block comes to rest after collision. When the initial velocity of the lighter block is v, then the value of coefficient of restitution (e) will be
View Solution
