A spring of certain length and having spring constant k is cut into two pieces of length in a ratio 1:2. The spring constants of the two pieces are in a ratio :
1:1
1:4
1:2
2:1
The correct Answer is:D
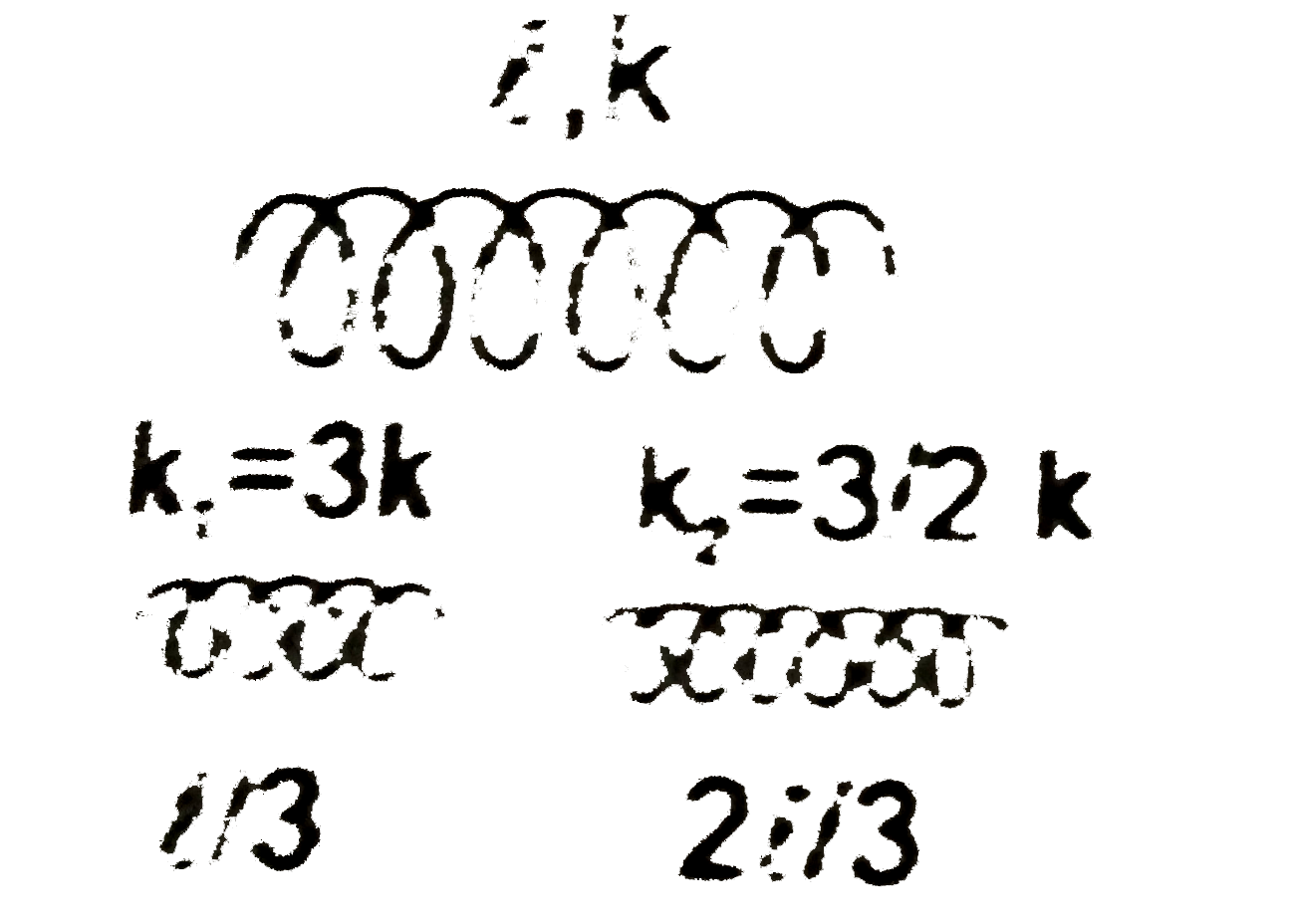
k1k2=3k3k/2=21Ans.(D)
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 88
Explore 7 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:Now answer the following :
Explore 20 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 86
Explore 6 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 54 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCEChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
Knowledge Check
A spring of constant K is cut into two parts of length in the ratio 2:3 . The spring constant of large spring is
A53KB23KCkD35kA spring of force constant k is cut into two pieces whose lengths are in the ratio 1:2. The force constant of the longer piece?
Ak/2B3k/2C2kD3kA spring fo spring constant k is broken in the length ratio 1:3. The spring constant of larger part will be
A4k/3B2k/3Ck/3D5k/3
If a spring of spring constant K is vcut into two parts A and B having lengths in the ratio of 1 : 4 .Calculate the ratio of spring constants of Aand B .
View SolutionA spring has length'l' and spring constant 'k'. It is cut into two pieces of lengths l1andl2 such that l1=nl2. The force constant of the spring of length l1 is
View SolutionA spring of spring constant k is cut in three equal pieces. The spring constant of each part will be
View SolutionAssertion A spring of force constatn k is cut in to two piece having lengths in the ratio 1:2 The force constant of series combination of the two parts is 3k2
The spring connected in series are represented by k=k1+k2
View SolutionA large magnet is broken into two pieces,so that their length are in the ratio 2:1.The pole strength of the two piece will be in the ratio
View Solution

