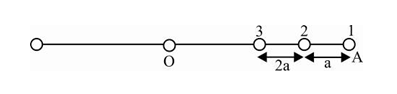
A particle moves with simple harmomonic motion in a straight line. In first τs, after starting from rest it travels a distance a, and in next τs it travels 2a, in same direction, then :-
amplitude of motion is 4a
time period of oscillations is 6π
time period of oscillations is 6π
time period of oscillations
The correct Answer is:B
As the particle starts from rest so we choose
x(t)=Acosωt
At t=0,x=A
When t=τ,x=A−a
when t=2τ,x=A−3a∴A−a=Acosωt
and A−3a=Acos2ωτ=A(2cos2ωt−1)
⇒(A−3a)=A[2(A−aA)2−1]⇒A−3aA=2(A−aA)2−1
on solving ,A=2a
Now A−a=Acosωτ, ⇒cosωτ=−12=cosπ3⇒ωτ=π3⇒
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:7-previous year question
Explore 46 Videos
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:LEVEL (2)
Explore 40 Videos
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:JEE Advanced (Archive) (True/False Type)
Explore 3 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBook:VMC MODULES ENGLISHChapter:SYSTEM OF A PARTICLES & ROTATIONAL MOTIONExercise:IN-CHAPTER EXERCISE F
Explore 10 Videos
Similar Questions
A particle moves with simple harmonic motion in a straight line. In first τs, after starting form rest it travels a destance a, and in next τs it travels 2a, in same direction, then:
View SolutionA particle moves with a simple harmonic motion in a straight line, in the first second starting from rest it travels a distance a and in the next second it travels a distance b in the same direction. The amplitude of the motion is
View SolutionA particle performs SHM in a straight line. In the first second, starting from rest, it travels a distance a and in the next second it travels a distance b in the same side of mean position. The amplitude of the SHM is
View SolutionA particle experiences a constant acceleration for 20 sec after starting from rest. If it travels distance S1 in the first 10 sec and a distance S2 in the next 10 sec, Then
View SolutionA particle experiences a constant acceleration for 20 sec after starting from rest. If it travels distance S1 in the first 10 sec and a distance S2 in the next 10 sec, Then
View SolutionA particle start moving from rest state along a straight line under the action of a constant force and travel distance x in first 5 seconds. The distance travelled by it in next five seconds will be
View SolutionA particle starts moving from position of rest under a constant acceleration. If it travels a distance x in t second, what distance will it travel in next t second?
View SolutionA particle at rest starts moving in a horizontal straight line with a uniform acceleration. The ratio of the distances covered during the fourth and third seconds is
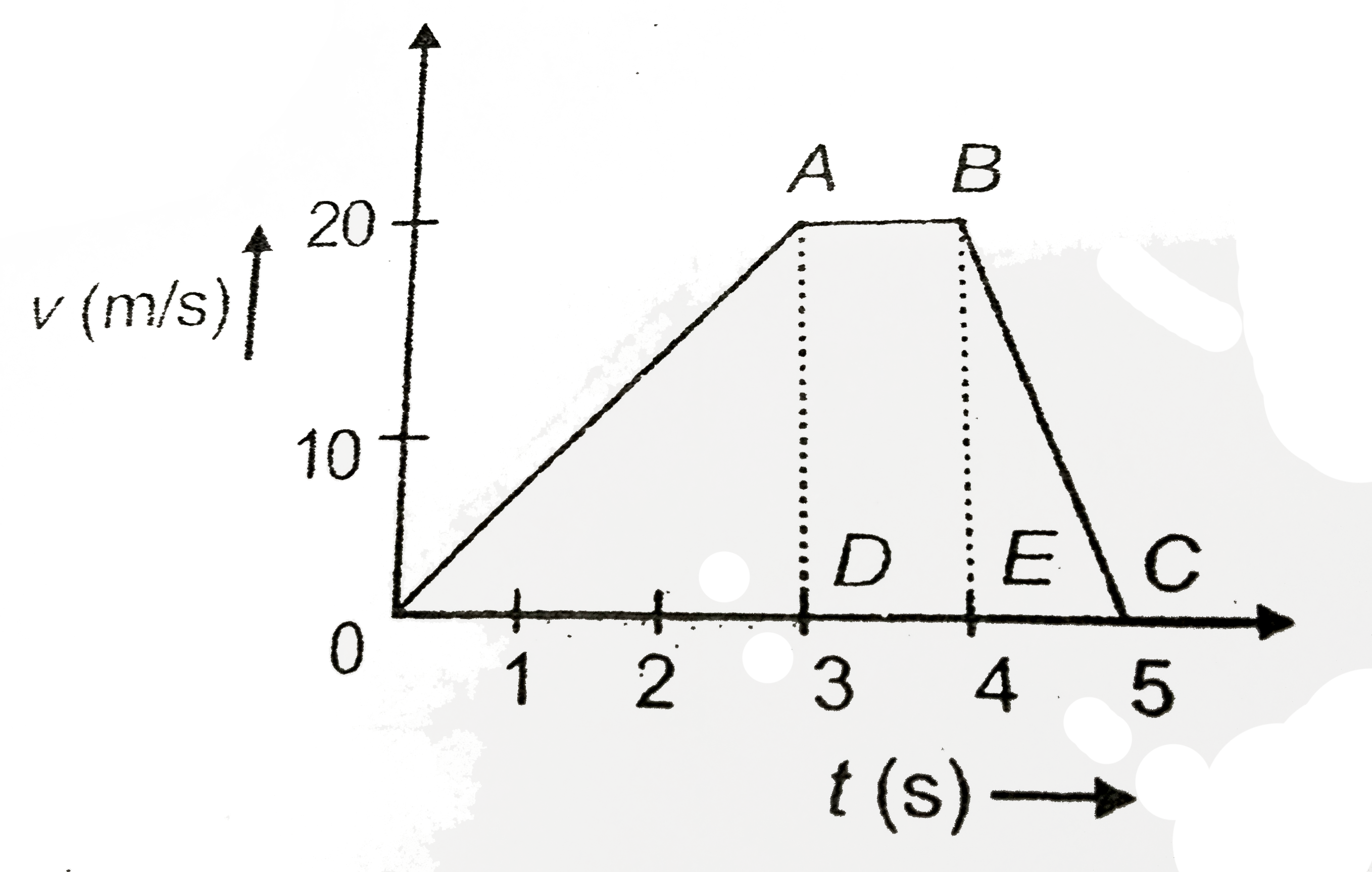
View SolutionThe variation of velocity of a particle moving along a straight line is as shown in the figure given below. The distance travelled by the particle in 5 s is
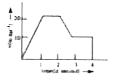
View SolutionThe variation of velocity of a particle moving along a straight line is shown in the figure. The distance travelled by the particle in 4s is
View Solution

