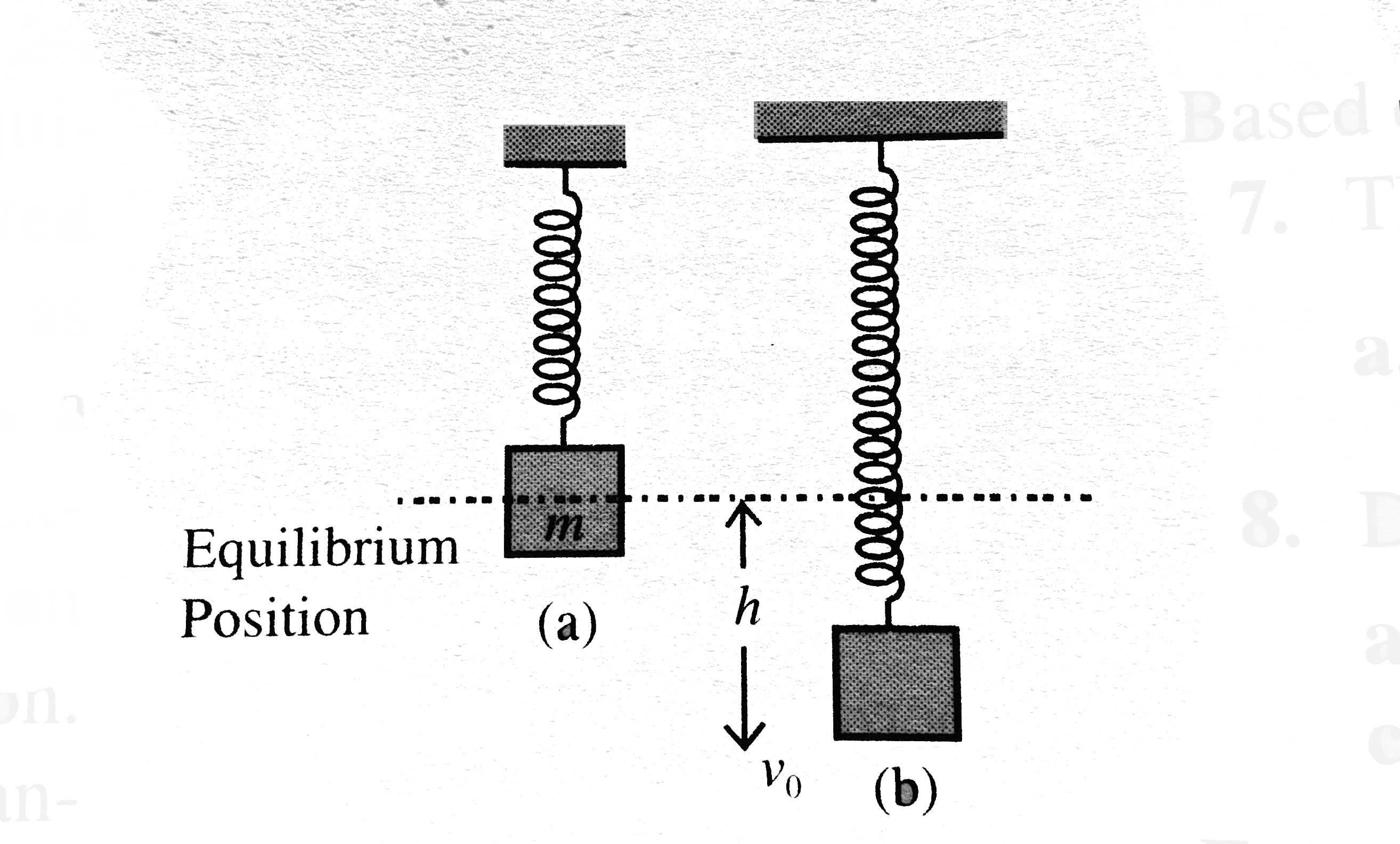
A block of mass m is connected to a spring constant k and is at rest in equilibrium as shown. Now, the block is Displacement by h below its equilibrium position and imparted a speed v0 towards down as shown in the Fig. As a result of the jerk, the block executes simple harmonic motion about its equilibrium position. Based on this information, answer the following question.
Q. The equation for the simple harmonic motion is
y=−Asin[√kmt+sin−1(hA)]
y=−Acos[√kmt+sin−1(hA)]
y=−Asin[√kmt+cos−1(hA)+π2]
y=−Asin[√kmt+cos−1(hA)+π4]
The correct Answer is:A
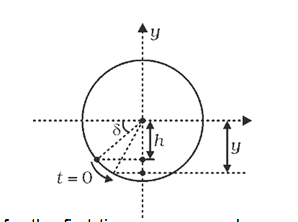
To have the equilibrium of simple harmonic motion, it is best to represent simple harmonic motion as uniform circular motion. At t=0 let particle is making an angle Σ with negative x-axis as shown, then
sinΣ=hA⇒Σ=sin−1(hA)
At time t, y=−Asin(ωt+Σ)
So the equation of simple harmonic motion is y=−√mv20k+h2{sin[√kmt+sin−1(hA)]}
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 6-previous year question56videos
SIMPLE HARMONIC MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question46videos
SIMPLE HARMONIC MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL (1)75videos
SIMPLE HARMONIC MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)3videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F10videos
SYSTEM OF A PARTICLES & ROTATIONAL MOTION
Similar Questions
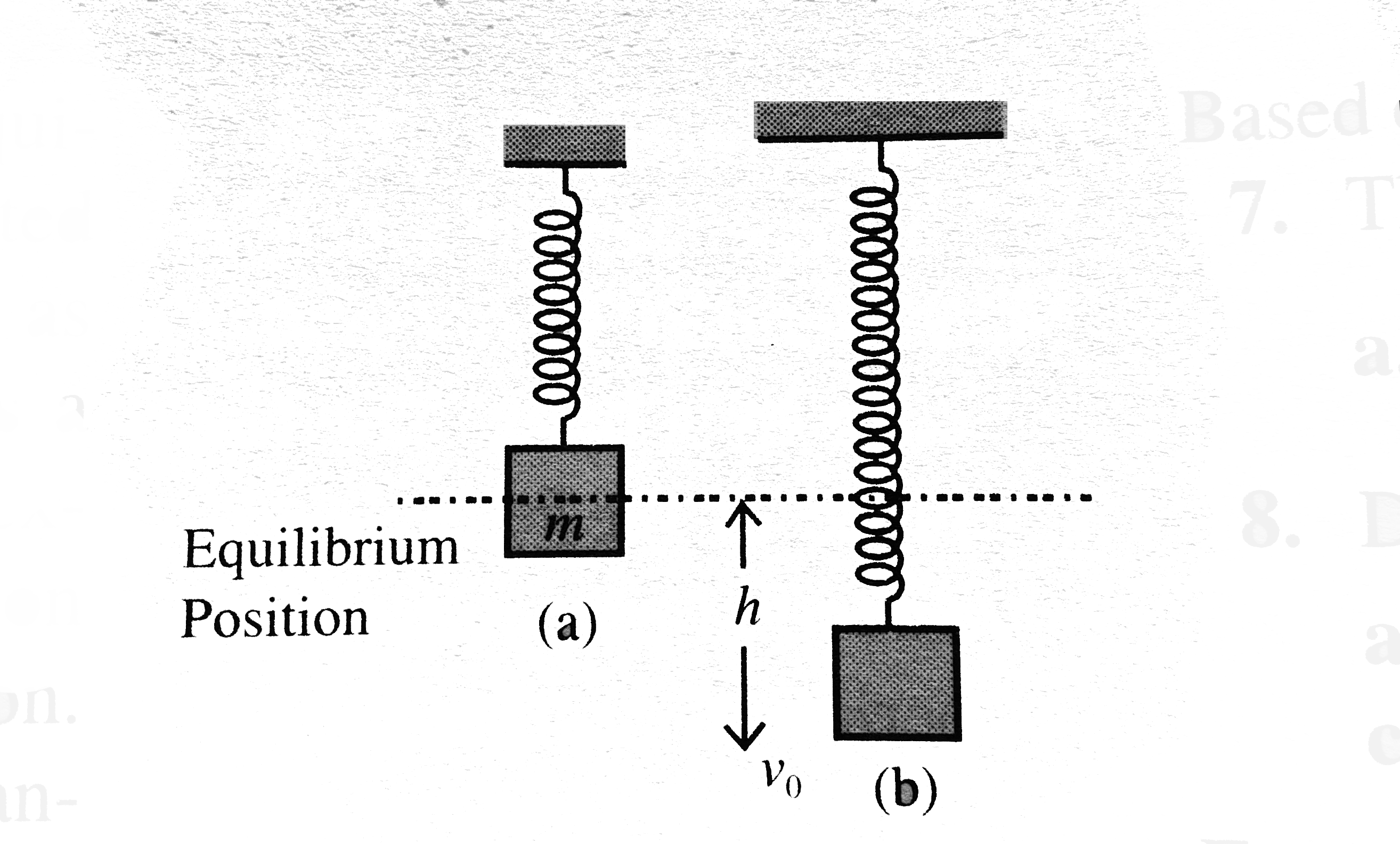
A block of mass m is connected to a spring constant k and is at rest in equilibrium as shown. Now, the block is Displacement by h below its equilibrium position and imparted a speed v0 towards down as shown in the Fig. As a result of the jerk, the block executes simple harmonic motion about its equilibrium position. Based on this information, answer the following question.
Q. The amplitude of oscillation isView Solution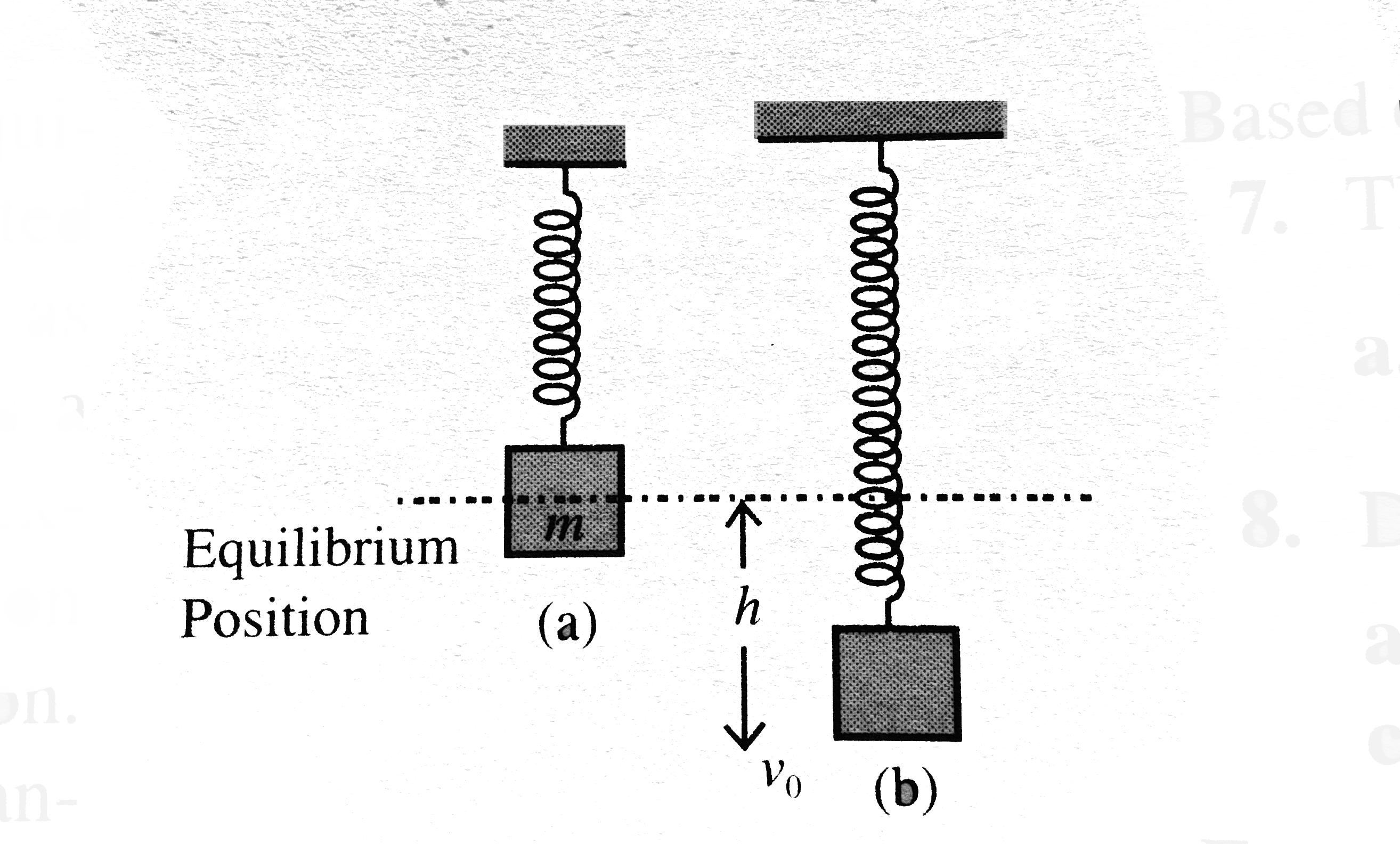
A block of mass m is connected to a spring constant k and is at rest in equilibrium as shown. Now, the block is Displacement by h below its equilibrium position and imparted a speed v0 towards down as shown in the Fig. As a result of the jerk, the block executes simple harmonic motion about its equilibrium position. Based on this information, answer the following question.
Q. Find the amplitude.View Solution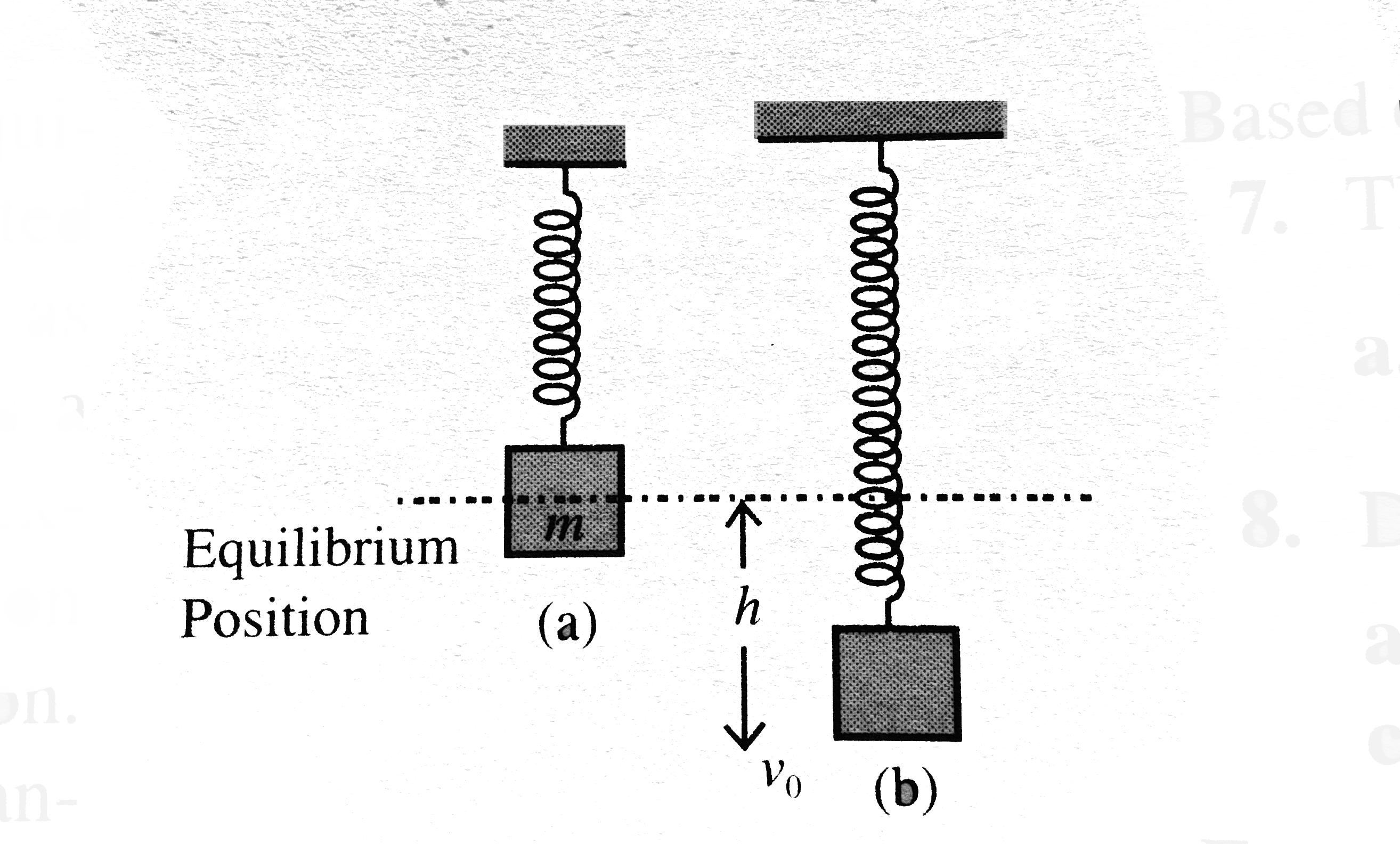
A block of mass m is connected to a spring constant k and is at rest in equilibrium as shown. Now, the block is Displacement by h below its equilibrium position and imparted a speed v0 towards down as shown in the Fig. As a result of the jerk, the block executes simple harmonic motion about its equilibrium position. Based on this information, answer the following question.
Q. Find the time taken by the block to cross the mean position for the first time.View SolutionA block of mass m is suspended through a spring of spring constant k and is in equilibrium. A sharp blow gives the block an initial downward velocity v. How far below the equilibrium position, the block comes to an instantaneous rest?
View SolutionThe progress of the reaction A→nB with time t is shown in Fig.
From this information answer the following questions
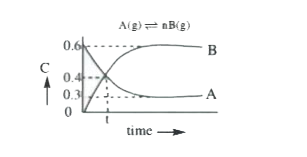
The equilibrium constant KC isView SolutionA block of mass m is connected two springs of spring constant 2k annd k , respectively , as shown in the vertical plane. At equilibrium , both springs are compressed by same length. If suddenly lower spring is cut, then acceleration of block, just after spring cut , is
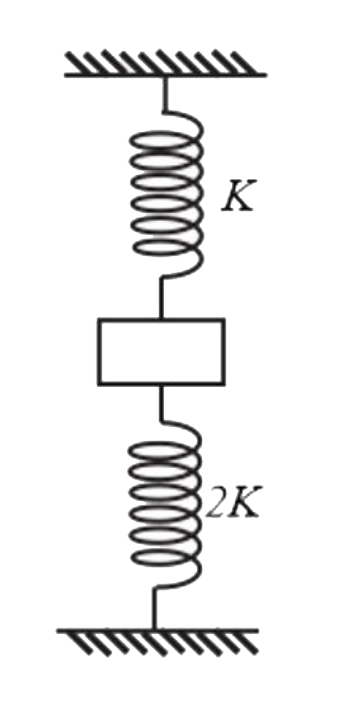 View Solution
View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.
 View Solution
View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.
 View Solution
View SolutionA block of mass m is connected with two ideal pullies and a massless spring of spring constant K as shown in figure. The block is slightly displaced from its equilibrium position. If the time period of oscillation is μπ√mK. Then find the value of μ.
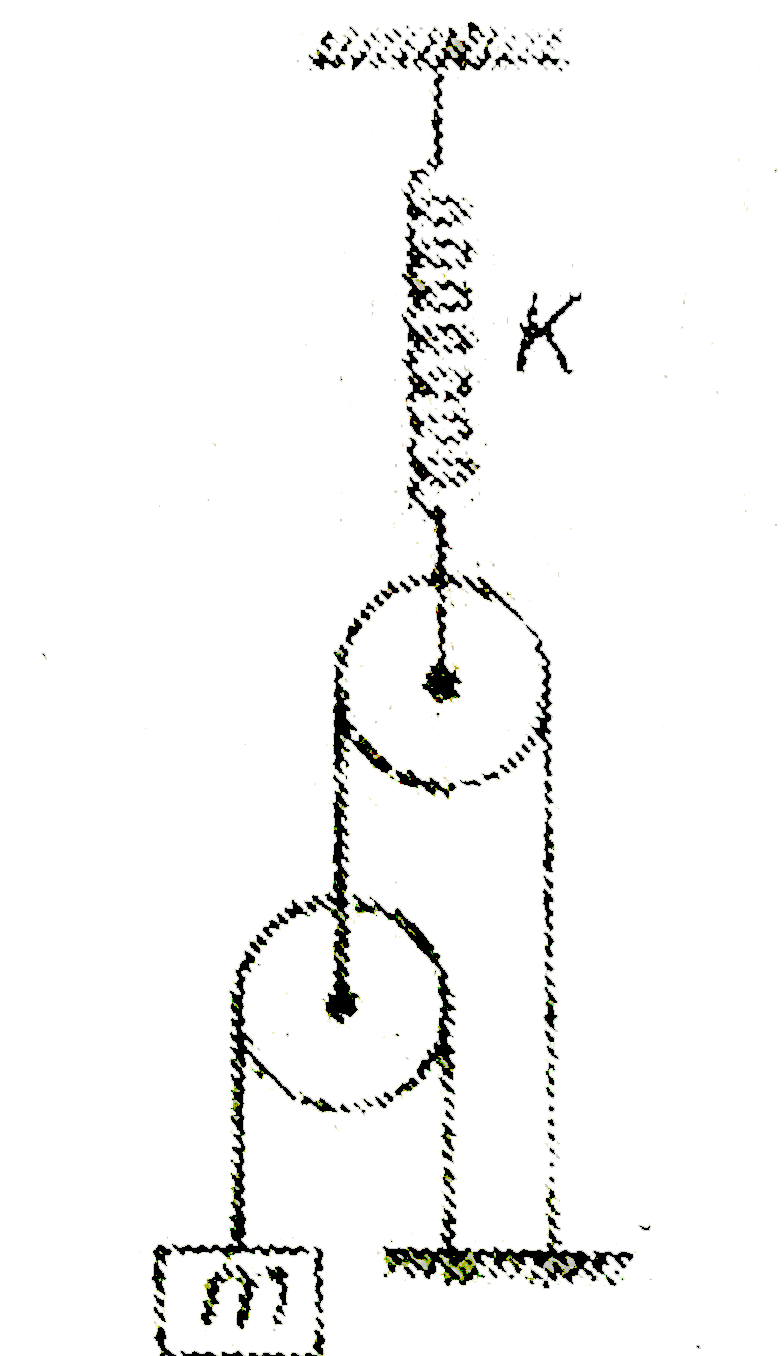 View Solution
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View Solution
