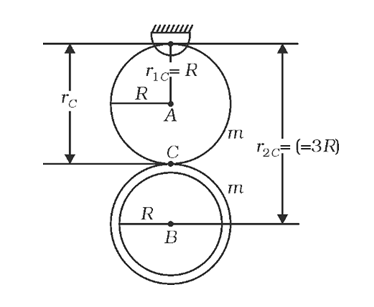
A uniform dics of mass m and radius $R = \frac{80}{23 π^{2}}$ m is pivoted smoothly at $P$ . If a uniform ring of mass $m$ and radius $R$ is welded at the lowest point of the disc, find the period of $S H M$ of the system (disc $+$ ring). (in seconds)

Video Solution

Text Solution

Verified by Experts

The correct Answer is:2

The time period of a physical pendulum is $T = 2 π \sqrt{\frac{I_{p}}{M g r}}$
Here we have three quantities $I_{p}$ ,m and r.
Let us calculate the quantities one by one as follows:
Finding $I_{p} : I_{p} = {(I_{p})}_{r i n g}$
$w h e r e {(I_{p})}_{r \in g} = I_{A} + m {(P A)}_{2} = \frac{m R^{2}}{2} + m R^{2} = \frac{3 m R^{2}}{2}$ and ${(I_{p})}_{r \in g} = I_{B} + m {(P B)}^{2} = m R^{2} + m (3 R^{2}) = 10 m R^{2}$ Then, we have $I_{p} = \frac{3}{2} m R^{2} = 10 m R^{2} = \frac{23}{2} m R^{2}$
Finding r, $r = 2$

Updated on:21/07/2023

|

Class 12 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

VMC MODULES ENGLISH-SIMPLE HARMONIC MOTION -LEVEL (2)

Home
Ask Doubt
Profile