Question

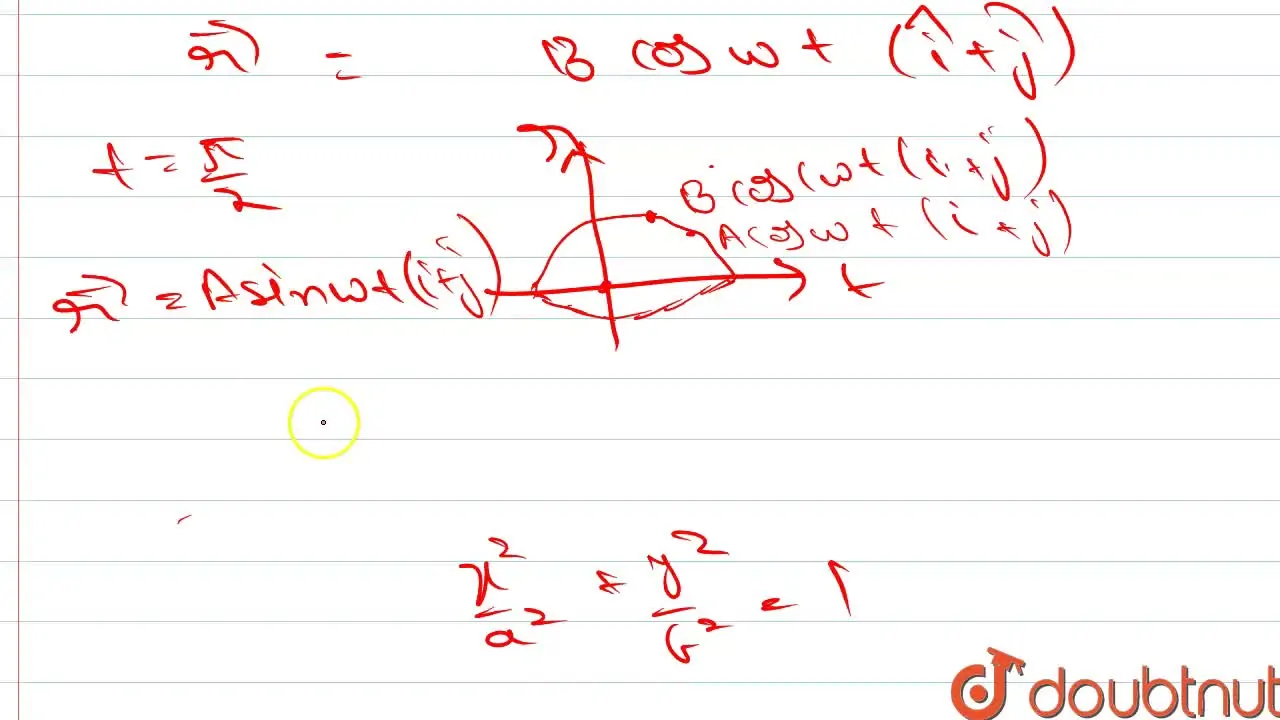
A particle moves in x-y plane according to the equation $\overrightarrow{r}=(A\sin \omega t+B\cos \omega t)(\hat{i}+\hat{j})$ :

Options

A. SHM and along a straight line
B. SHM and along an elliptical path
C. SHM and along a circular path
D. Not SHM, but periodic

Answer

A

Explanation

To solve the problem step by step, we will analyze the motion of the particle given by the vector equation:

$$\overrightarrow{r}=\left(A\sin \right(\omega t)+B\cos (\omega t\left)\right)\hat{i}+\hat{j}$$

Step 1: Identify the components of the motion

The position vector \(\vec{r}\) can be broken down into its x and y components:
- \(x(t) = A \sin(\omega t) + B \cos(\omega t)\)
- \(y(t) = 1\) (since the j component is constant)

Step 2: Determine the velocity components

To find the velocity, we differentiate the position components with respect to time \(t\):

\( v_x = \frac{dx}{dt} = \frac{d}{dt}(A \sin(\omega t) + B \cos(\omega t)) = A \omega \cos(\omega t) - B \omega \sin(\omega t) \)

\( v_y = \frac{dy}{dt} = 0 \)

Step 3: Determine the acceleration components

Next, we differentiate the velocity components to find the acceleration:

\( a_x = \frac{dv_x}{dt} = \frac{d}{dt}(A \omega \cos(\omega t) - B \omega \sin(\omega t)) = -A \omega^2 \sin(\omega t) - B \omega^2 \cos(\omega t) \)

\( a_y = \frac{dv_y}{dt} = 0 \)

Step 4: Check for Simple Harmonic Motion (SHM)

For SHM, the acceleration must be proportional to the displacement and directed towards the equilibrium position. The general form for SHM is:

\( a = -\omega^2 x \)

In our case, we can express the acceleration in terms of \(x(t)\):

\( a_x = -\omega^2 (A \sin(\omega t) + B \cos(\omega t)) \)

This shows that the motion in the x-direction is indeed SHM since the acceleration is proportional to the displacement \(x(t)\).

Step 5: Determine the path of motion

To determine the path, we can analyze the relationship between \(x\) and \(y\). Since \(y\) is constant (equal to 1), the motion will be constrained to a horizontal line at \(y = 1\).

To find the relationship between \(x\) and \(y\), we can express \(x\) in terms of \(y\):

\( y = 1 \implies \text{The particle moves horizontally, changing only in the x-direction.} \)

Conclusion

1. The particle performs Simple Harmonic Motion (SHM) in the x-direction.
2. The path of the particle is along a straight line at \(y = 1\).