Explain
(i) Undamped and damped oscillations and
(ii) free, forced and resonant oscillations with illustrations.
Step-by-Step Solution
1. Definition of Undamped Oscillations:
- Undamped oscillations are oscillations where the amplitude remains constant over time. This means that the energy of the system is conserved, and there are no external forces acting to dissipate energy (like friction or air resistance).
- Illustration: A mass attached to a spring that is oscillating in a vacuum (where there is no air resistance) is an example of undamped oscillation. The mass will continue to oscillate indefinitely with the same amplitude.
2. Definition of Damped Oscillations:
- Damped oscillations are those in which the amplitude decreases over time due to the presence of a damping force (like friction or air resistance). As time progresses, the energy of the system is lost, leading to a gradual reduction in amplitude.
- Illustration: A swinging pendulum in air experiences air resistance, which causes it to lose energy and gradually come to a stop. The amplitude of the pendulum's swing decreases over time, demonstrating damped oscillation.
Part (ii): Free, Forced, and Resonant Oscillations
1. Free Oscillations:
- Free oscillations occur when a system oscillates without any external force acting on it after being displaced from its equilibrium position. The system oscillates at its natural frequency.
- Illustration: A pendulum that is pulled to one side and then released will swing back and forth at its natural frequency, which is determined by its length.
2. Forced Oscillations:
- Forced oscillations occur when an external periodic force is applied to a system. The system oscillates at the frequency of the external force rather than its natural frequency.
- Illustration: If you push a child on a swing at regular intervals, the swing will oscillate at the frequency of your pushes, even if it is different from its natural frequency.
3. Resonant Oscillations:
- Resonant oscillations occur when the frequency of the external force matches the natural frequency of the system. This results in a significant increase in amplitude.
- Illustration: If you push a swing at just the right moment (matching its natural frequency), the swing will go higher and higher with each push, illustrating resonance.
- Undamped oscillations are oscillations where the amplitude remains constant over time. This means that the energy of the system is conserved, and there are no external forces acting to dissipate energy (like friction or air resistance).
- Illustration: A mass attached to a spring that is oscillating in a vacuum (where there is no air resistance) is an example of undamped oscillation. The mass will continue to oscillate indefinitely with the same amplitude.
- Damped oscillations are those in which the amplitude decreases over time due to the presence of a damping force (like friction or air resistance). As time progresses, the energy of the system is lost, leading to a gradual reduction in amplitude.
- Illustration: A swinging pendulum in air experiences air resistance, which causes it to lose energy and gradually come to a stop. The amplitude of the pendulum's swing decreases over time, demonstrating damped oscillation.
- Free oscillations occur when a system oscillates without any external force acting on it after being displaced from its equilibrium position. The system oscillates at its natural frequency.
- Illustration: A pendulum that is pulled to one side and then released will swing back and forth at its natural frequency, which is determined by its length.
- Forced oscillations occur when an external periodic force is applied to a system. The system oscillates at the frequency of the external force rather than its natural frequency.
- Illustration: If you push a child on a swing at regular intervals, the swing will oscillate at the frequency of your pushes, even if it is different from its natural frequency.
- Resonant oscillations occur when the frequency of the external force matches the natural frequency of the system. This results in a significant increase in amplitude.
- Illustration: If you push a swing at just the right moment (matching its natural frequency), the swing will go higher and higher with each push, illustrating resonance.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL 0 LONG ANSWER TYPE
2 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL (1)
75 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL 0 SHORT ANSWER TYPE - I
8 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)
3 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
Similar Questions
Knowledge Check
At resonance, the amplitude of forced oscillations is
AminimumBmaximumCzeroDnone of theseIn case of force oscillations of a body
Adriving force is constant throughout.Bdriving force is to be applied only momentarilyCdriving force has to be periodic and continuousDdriving force is not required.
Is an oscillation a wave? Explain.
View SolutionExplain (i) natural oscillation (ii) natural frequency.
View SolutionIn damped oscillation graph between velocity and position will be : -
View SolutionWhat are forced oscillations? Why are they called so ?
View SolutionTwo pendulums C and D suspended from a wire as shown in the figure given below. Pendulum C is made to oscillate by displacing it from its mean position. It is seen that D also starts oscillating.
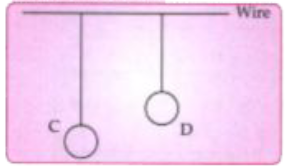
(i) Name the type of oscillation, C will execute.
(ii) Name the type of oscillation, D will execute.
(iii) If the length of D is made equal to C then what difference will you notice in the oscillations of D?
(iv) What is the name of the phenomenon when the length of D is made equal to C?
View SolutionA particle is performing damped oscillation with frequency 5Hz. After every 10 oscillations its amplitude becmoes half. Find time from beginning after which the amplitude becomes 1/1000 of its initial amplitude :
View Solution
