A solid cylinder of mass m is attached to a horizontal spring with force constant k. The cylinder can roll without slipping along the horizontal plane. (See the accompanying figure.) Show that the center of mass of the cylinder executes simple harmonic motion with a period T=2π√3m2k, if displaced from mean position.

(i) Time period ,T=2s
Amplitude,A=3cm
At time, t=0, the radius vector OP makes an angle π2 with the positive x-asix, i.e., phase Angle ϕ=+π2
Therefore, the equation of simple harmonic motion for the x-projection of OP,at time t, is given by the displacement equation:
x=Acos[2πtT+ϕ]=3cos(2πt2+π2)=−3sin(2πt2)
x=−3sinπtcm
(ii) Time period , T=4s
Amplitude, a=2m
At time t=0, OP makes an angle pi with the x-axis, in the anticlockwise direction. Hence phase angle ,ϕ=+π Therefore, the equation of simple harmonic motion for the x-proection of Op,at time t,is given as:
x=acos(2πtT+ϕ)=2cos(2πt4+π)
x=−2cos(πt2)m
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:LEVEL 0 LONG ANSWER TYPE
Explore 2 Videos
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:LEVEL (1)
Explore 75 Videos
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:LEVEL 0 SHORT ANSWER TYPE - I
Explore 8 Videos
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:JEE Advanced (Archive) (True/False Type)
Explore 3 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBook:VMC MODULES ENGLISHChapter:SYSTEM OF A PARTICLES & ROTATIONAL MOTIONExercise:IN-CHAPTER EXERCISE F
Explore 10 Videos
Similar Questions
A solid sphere of mass m is attached to a light spring of force constant k so that it can roll without slipping along a horizontal surface. Calculate the period of oscillation made by sphere.

View SolutionA solid cylinder attached to horizontal massless spring can roll without slipping along a horizontal surface. Find time period of oscillation.
View SolutionA solid cylinder of mass M and radius R rolls without slipping down an inclined plane of length L and height h. What is the speed of its center of mass when the cylinder reaches its bottom
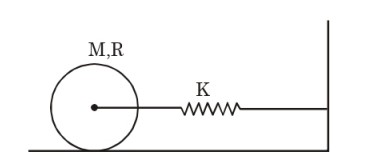
View SolutionA solid uniform cylinder of mass M attached to a massless spring of force constant k is placed on a horizontal surface in such a way that cylinder can roll without slipping. If system is released from the stretched position of the spring, then the period will be-
_E01_059_Q01.png)
View Solution
A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder is
View SolutionA solid cylinder of mass M and radius R rolls without slipping on a flat horizontal surface. Its moment of inertia about the line of contact is
View Solution
A uniform solid cylinder having mass M and radius R is pulled by a horiozntal force F acting through the center as shown. The cylinder rolls to the right without slipping. What is the magnitude of the force of friction between the cylinder and the ground?
View SolutionA particle of mass 3 kg , attached to a spring with force constant 48Nm−1execute simple harmonic motion on a frictionless horizontal surface. The time period of oscillation of the particle, is seconds , is
View SolutionConsider the situation in which one end of a massless spring of spring constant k is connected to a cylinder of mass m and the other to a rigid support. When cylinder is given a gentle push in horizontal direction it starts oscillating on the rough horizontal surface. During the oscillation cylinder rolls without slipping. When calculated, motion of cylinder is found to be S.H.M. with time period T=2π√3m2K and equation of SHM is x=Asinωt, where symbols have their usual meaning.

:
Q The minimum value of coefficient of friction such that the cylinder does not slip on the surface is:
View SolutionConsider the situation in which one end of a massless spring of spring constant k is connected to a cylinder of mass m and the other to a rigid support. When cylinder is given a gentle push in horizontal direction it starts oscillating on the rough horizontal surface. During the oscillation cylinder rolls without slipping. When calculated, motion of cylinder is found to be S.H.M. with time period T=2π√3m2K and equation of SHM is x=Asinωt, where symbols have their usual meaning.
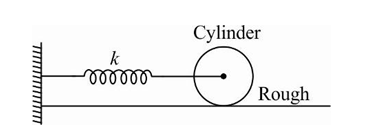
At a distance x1 from the equilibrium position, kinetic energy of the oscillating system becomes equal to potential energy then, x1is equal to:
View Solution

