In case of damped oscillation frequency of oscillation is
greater than natural frequency
less than natural frequency
equal to nature frequency
Both (a) and (b)
The correct Answer is:B
To solve the question regarding the frequency of oscillation in the case of damped oscillation, we will follow these steps:
1. Understand the Forces Acting on the Oscillator:
In a simple harmonic motion (SHM), the primary force acting on the mass (M) is the restoring force from the spring, which is given by Hooke's Law:
Fspring=−kx
where k is the spring constant and x is the displacement from the equilibrium position.
2. Introduce Damping Force:
In the case of damped oscillation, there is an additional damping force acting on the mass, which opposes the motion. This force can be expressed as:
Fdamping=−bv
where b is the damping constant and v is the velocity of the mass.
3. Calculate the Net Force:
The net force acting on the mass can be expressed as the sum of the spring force and the damping force:
Fnet=Fspring+Fdamping=−kx−bv
4. Set Up the Equation of Motion:
According to Newton's second law, the net force is also equal to the mass times acceleration:
Md2xdt2=−kx−bdxdt
Rearranging this gives us:
Md2xdt2+bdxdt+kx=0
5. Identify the Damped Angular Frequency:
The equation of motion for damped oscillations can be compared to the standard form of a second-order linear differential equation. The damped angular frequency ωd can be derived from the equation:
ωd=√km−(b2m)2
Here, km is the square of the natural frequency ω20.
6. Relate Damped Frequency to Natural Frequency:
The damped frequency fd can be related to the damped angular frequency as follows:
fd=ωd2π
Since ωd<ω0, it follows that:
fd<f0
where f0 is the natural frequency of the system.
Conclusion:
In the case of damped oscillation, the frequency of oscillation is less than the natural frequency of the system. Therefore, the correct answer is that the damped frequency fd is less than the natural frequency f0.
---
In a simple harmonic motion (SHM), the primary force acting on the mass (M) is the restoring force from the spring, which is given by Hooke's Law:
Fspring=−kx
where k is the spring constant and x is the displacement from the equilibrium position.
In the case of damped oscillation, there is an additional damping force acting on the mass, which opposes the motion. This force can be expressed as:
Fdamping=−bv
where b is the damping constant and v is the velocity of the mass.
The net force acting on the mass can be expressed as the sum of the spring force and the damping force:
Fnet=Fspring+Fdamping=−kx−bv
According to Newton's second law, the net force is also equal to the mass times acceleration:
Md2xdt2=−kx−bdxdt
Rearranging this gives us:
Md2xdt2+bdxdt+kx=0
The equation of motion for damped oscillations can be compared to the standard form of a second-order linear differential equation. The damped angular frequency ωd can be derived from the equation:
ωd=√km−(b2m)2
Here, km is the square of the natural frequency ω20.
The damped frequency fd can be related to the damped angular frequency as follows:
fd=ωd2π
Since ωd<ω0, it follows that:
fd<f0
where f0 is the natural frequency of the system.
In the case of damped oscillation, the frequency of oscillation is less than the natural frequency of the system. Therefore, the correct answer is that the damped frequency fd is less than the natural frequency f0.
Similar Questions
A small magnetic needle performs 10 oscillations/minute in the earth's horizontal magnetic field . When a bar magnet is placed near the small magnet in same position , frequency of oscillations becomes 10√2 oscillations/minute . If the bar magnet be turned around end to end , the rate of oscillation of small magnet will become
View SolutionGive examples of damped oscillation.
View Solution
Knowledge Check
In case of force oscillations of a body
Adriving force is constant throughout.Bdriving force is to be applied only momentarilyCdriving force has to be periodic and continuousDdriving force is not required.
A damped harmonic oscillator has a frequency of 5 oscillations per second . The amplitude drops to half its value for every 10 oscillation. The times it will take to drop to 11000 of the original amplitude is close to:
View SolutionA mass m is suspended from a spring. Its frequency of oscillation is f. The spring is cut into two halves and the same mass is suspended from one of the pieces of the spring. The frequency of oscillation of the mass will be
View SolutionThere is a LCR circuit , If it is compared with a damped oscillation of mass m oscillating with force constant k and damping coefficient 'b'. Compare the terms of damped oscillation with the devices in LCR circuit.
View SolutionIn damped oscillation graph between velocity and position will be : -
View SolutionThe velocity-time diagram of a harmonic oscillator is shown in the adjoining figure. The frequency of oscillation is
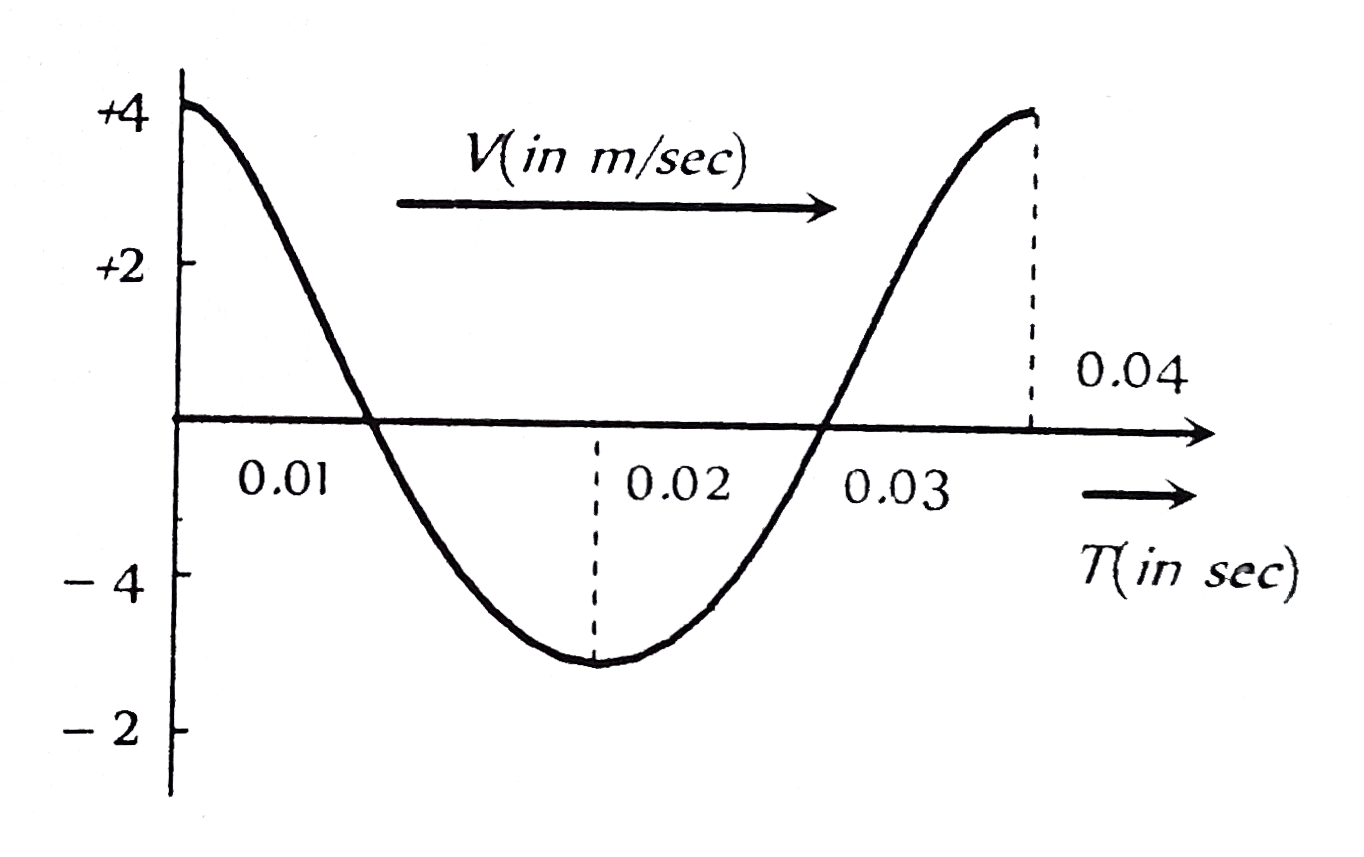
View SolutionA spring mass system oscillates in a car. If the car accelerates on a horizontal road, the frequency of oscillation will
View SolutionAn LC series circuit has an oscillation frequency f. Two isolated inductors, each with inductance L and two capacitors each with capacitance C, all are connected in series and circuit is completed. The oscillation frequency is
View Solution
