A body is thrown with the velocity v0 at an angle of θ to the horizontal. Determine v0inms−1 if the maximum height attained by the body is 5m and at the highest point of its trajectory the radius of curvature is r=3m. Neglect air resistance. [Use√80=9].
The correct Answer is:9
To solve the problem, we will follow these steps:
Step 1: Understand the relationship between maximum height and initial velocity
The maximum height h attained by a projectile is given by the formula:
h=v20sin2θ2g
where g is the acceleration due to gravity (approximately 10m/s2).
Step 2: Substitute the known values into the height equation
Given that the maximum height h=5m:
5=v20sin2θ2×10
This simplifies to:
5=v20sin2θ20
Multiplying both sides by 20 gives:
100=v20sin2θ
Thus, we have:
v20sin2θ=100(Equation 1)
Step 3: Use the radius of curvature at the highest point
At the highest point of the trajectory, the radius of curvature r is given by:
v2g=r
At the highest point, the vertical component of the velocity is zero, and the horizontal component is v0cosθ. Therefore, we can write:
(v0cosθ)2g=r
Substituting g=10m/s2 and r=3m:
(v0cosθ)210=3
This simplifies to:
(v0cosθ)2=30(Equation 2)
Step 4: Relate sin2θ and cos2θ
From the Pythagorean identity, we know:
sin2θ+cos2θ=1
Let cos2θ=x. Then sin2θ=1−x.
Step 5: Substitute sin2θ and cos2θ into the equations
From Equation 1:
v20(1−x)=100(Equation 3)
From Equation 2:
v20x=30(Equation 4)
Step 6: Solve the equations simultaneously
From Equation 4, we can express v20:
v20=30x
Substituting this into Equation 3:
30x(1−x)=100
Multiplying through by x gives:
30(1−x)=100x
Expanding and rearranging:
30−30x=100x
30=130x
x=30130=313
Step 7: Find v20
Substituting x back into Equation 4:
v20=30313=30⋅133=130
Thus:
v0=√130≈11.4m/s
Final Answer
The initial velocity v0 is approximately 11.4m/s.
---
The maximum height h attained by a projectile is given by the formula:
h=v20sin2θ2g
where g is the acceleration due to gravity (approximately 10m/s2).
Given that the maximum height h=5m:
5=v20sin2θ2×10
This simplifies to:
5=v20sin2θ20
Multiplying both sides by 20 gives:
100=v20sin2θ
Thus, we have:
v20sin2θ=100(Equation 1)
At the highest point of the trajectory, the radius of curvature r is given by:
v2g=r
At the highest point, the vertical component of the velocity is zero, and the horizontal component is v0cosθ. Therefore, we can write:
(v0cosθ)2g=r
Substituting g=10m/s2 and r=3m:
(v0cosθ)210=3
This simplifies to:
(v0cosθ)2=30(Equation 2)
From the Pythagorean identity, we know:
sin2θ+cos2θ=1
Let cos2θ=x. Then sin2θ=1−x.
From Equation 1:
v20(1−x)=100(Equation 3)
From Equation 2:
v20x=30(Equation 4)
From Equation 4, we can express v20:
v20=30x
Substituting this into Equation 3:
30x(1−x)=100
Multiplying through by x gives:
30(1−x)=100x
Expanding and rearranging:
30−30x=100x
30=130x
x=30130=313
Substituting x back into Equation 4:
v20=30313=30⋅133=130
Thus:
v0=√130≈11.4m/s
The initial velocity v0 is approximately 11.4m/s.
Topper's Solved these Questions
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Main (Archive)
Explore 19 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Advanced (Archive)
Explore 19 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:Long Answer Type
Explore 5 Videos
- Motion in Straight Line Book:VMC MODULES ENGLISHChapter:Motion in Straight Line Exercise:IN-CHAPTER EXERCISE-J
Explore 10 Videos
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:IN-CHAPTER EXERCISE-K
Explore 10 Videos
Similar Questions
A body is thrown with the velocity v0 at an angle of θ to the horizon. Determine v0inms−1 if the maximum height attained by the body is 5m and at the highest point of its trajectory the radius of curvature is r=3m. Neglect air resistance. [Use√80as9].
View SolutionA particle of mass m is projected with velocity v at an angle θ with the horizontal. Find its angular momentum about the point of projection when it is at the highest point of its trajectory.
View Solution
Knowledge Check
A body is thrown with a velocity of 9.8 m/s making an angle of 30∘ with the horizontal. It will hit the ground after a time
A3 sB2sC1.5 sD1 s
Two bodies are thrown with the same initial velocity of 30 m/s. One at 17°, other at 73° to the horizontal. The sum of the maximum heights reached by them is [g = 10 m/s2]
View SolutionA body of mass m is projected with a velocity u at an angle θ with the horizontal. The angular momentum of the body, about the point of projection, when it at highest point on its trajectory is
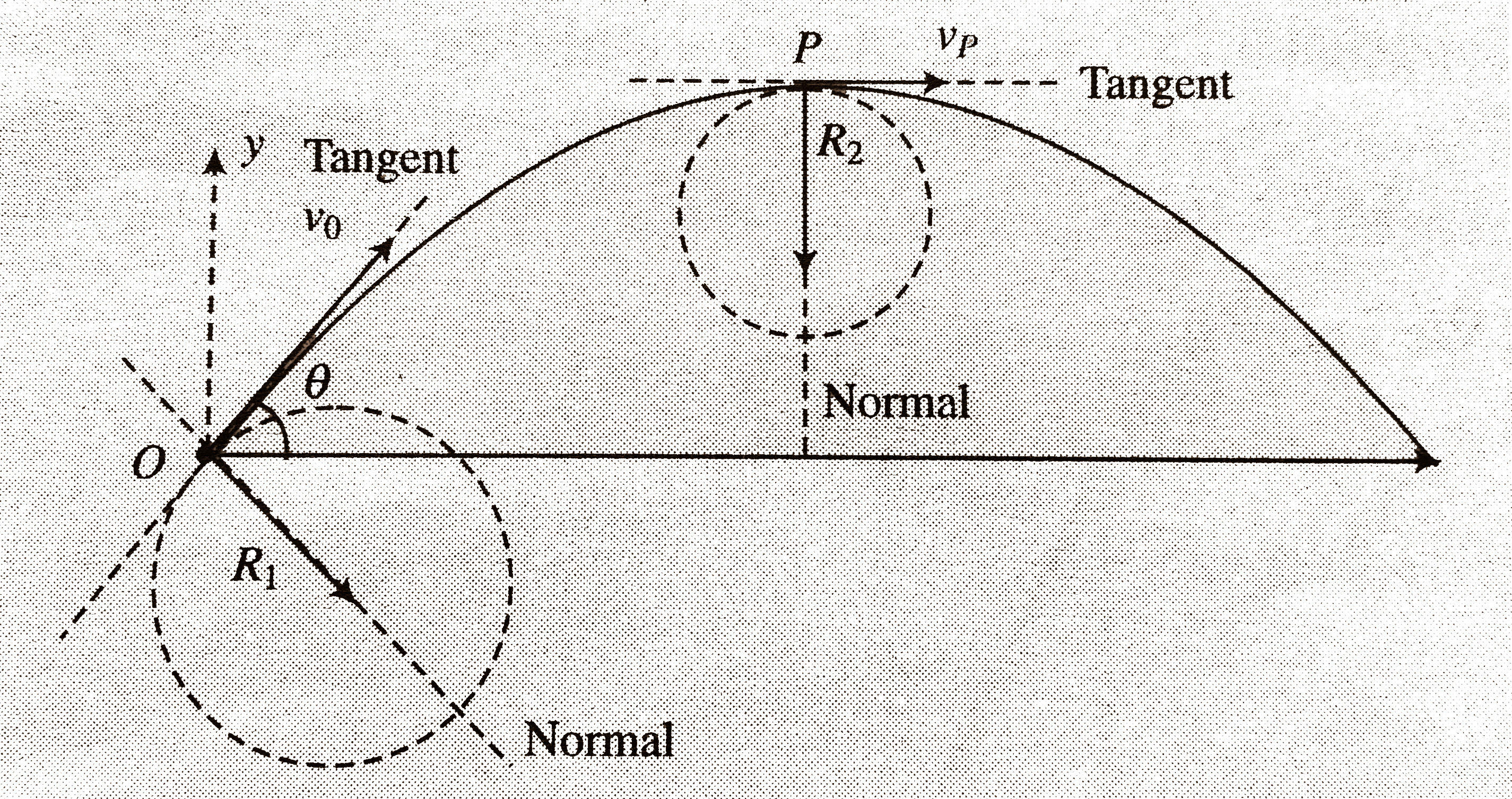
View SolutionA particle is projected at angle θ with horizontal with velocity v0att=0. Find
(a) tangential and normal acceleration of the particle at t=0 and at highest point of its trajectory.
(b) the radius of curvature a=0 and highest point.
 .
.
View SolutionA particle is thrown vertically upward. Its velocity at half of the height is 10 m/s. Then the maximum height attained by it : -
(g=10m/s2)
View SolutionA particle of mass m is projected with a velocity v at an angle of θ with horizontal. The angular momentum of the particle at the highest point of its trajectory is equal to :
View SolutionA javelin thrown into air at an angle with the horizontal has a range of 200 m. If the time of flight is 5 second, then the horizontal component of velocity of the projectile at the highest point of the trajectory is
View SolutionA particle is thrown vertically upwards. If its velocity is half of the maximum height is 20m/s, then maximum height attained by it is
View Solution