If PR = RQ, then :
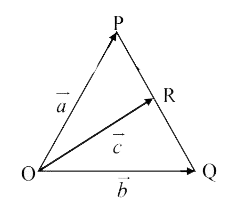
→a+→b=2→c
→a−→b=→c
→a−→b=2→c
→a+→b=→c
The correct Answer is:a
¯c=¯a+¯¯¯PR but ¯¯¯PR=¯¯¯RQ (equal in magnitude same in direction)
→¯c−¯a=¯b−¯c→¯a+¯b=2¯c
Topper's Solved these Questions
- INTRODUCTION TO VECTORS & FORCES Book:VMC MODULES ENGLISHChapter:INTRODUCTION TO VECTORS & FORCES Exercise:JEE Main ( ARCHIVE ) ( LEVEL-1)
Explore 12 Videos
- INTRODUCTION TO VECTORS & FORCES Book:VMC MODULES ENGLISHChapter:INTRODUCTION TO VECTORS & FORCES Exercise:JEE Advanced ( ARCHIVE LEVEL-2)
Explore 12 Videos
- INTRODUCTION TO VECTORS & FORCES Book:VMC MODULES ENGLISHChapter:INTRODUCTION TO VECTORS & FORCES Exercise:level 1
Explore 75 Videos
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:JEE Advance (Archive) TRUE/FALSE
Explore 1 Video
- JEE MAIN - 5Book:VMC MODULES ENGLISHChapter:JEE MAIN - 5Exercise:PART I : PHYSICS (SECTION - 2)
Explore 5 Videos
Similar Questions
two tangents RQ and RP are drawn from an external point R to the circle with centre O. If ∠PRQ=120∘ , then prove that OR= PR+ RQ
View SolutionRQ means
View SolutionRQ is
View SolutionIf P, Q and R are three points with coordinates (1,4),(4,5)and(m,m) respectively, then the value of m for which PR+RQ is minimum, is :
View SolutionIn a ΔPQR, N is a point on PR, such that QN⊥PR. If PN⋅NR=QN2, then prove that ∠PQR=90∘.
View SolutionPQRS is a rectangle such that PR+PQ=5PS and PR−PS=8. Then area (in sq. units) of rectangle is-
View SolutionGiven points P(2,3),Q(4,−2),andR(α,0). Find the value of a if PR+RQ is minimum.
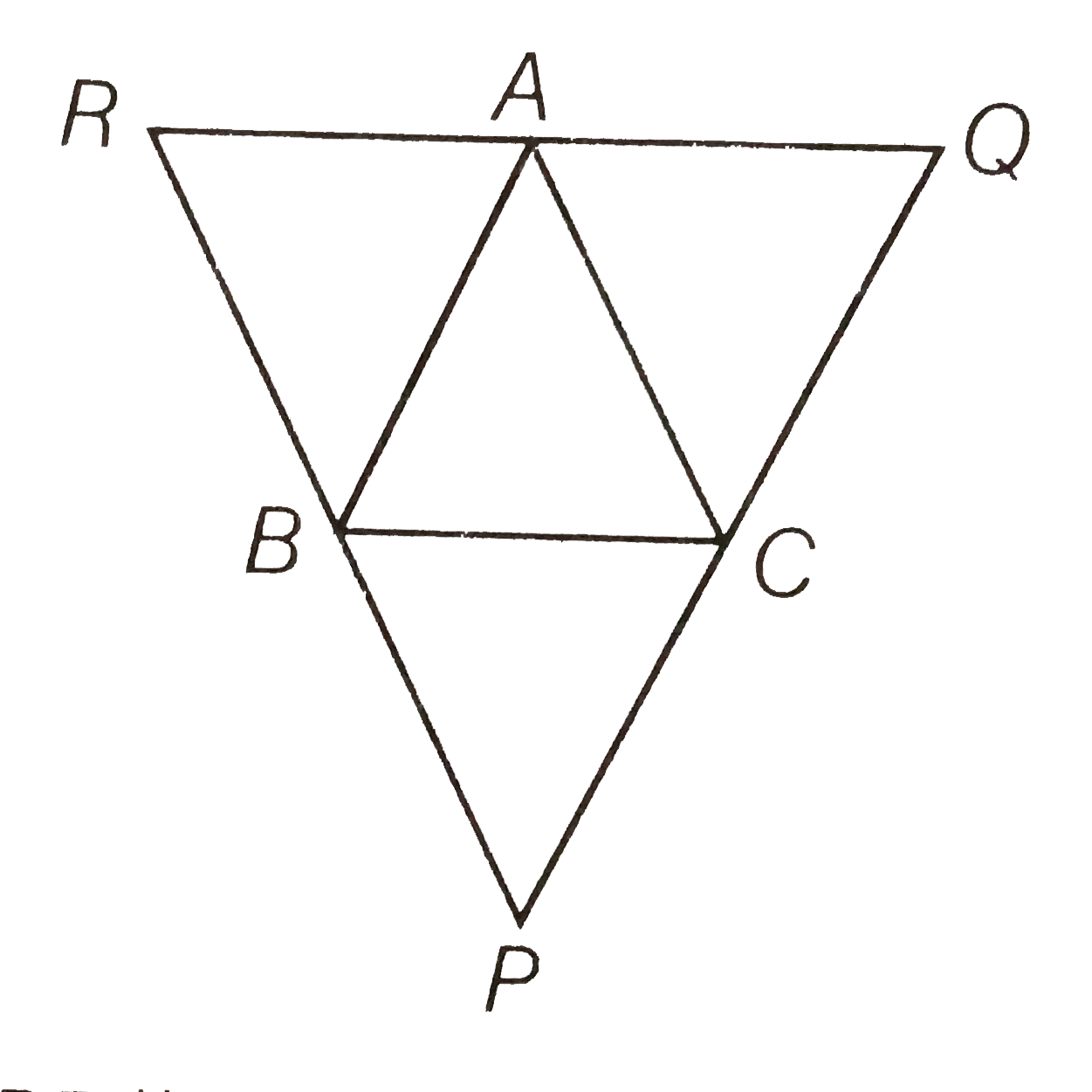
View SolutionThrough A, B and C lines RQ, PR and QP have been drawn, respectively parallel to sides BC, CA and AB of a ΔABC as shown in figure. Show that BC=12QR.
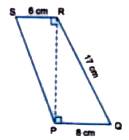
View SolutionCalculate the area of the quadrilateral PQRS shown in the adjoining figure, it being given that PR = 8 cm , RQ = 17 cm , ∠RPQ=90∘,RS=6cmand∠PRS=90∘
View SolutionLet P be a point on the ellipse x2a2+y2b2=1,0<b<a and let the line parallel to y-axis passing through P meet the circle x2+y2=a2 at the point Q such that P and Q are on the same side of x-axis. For two positive real numbers r and s, find the locus of the point R on PQ such that PR:RQ=r:s and P varies over the ellipse.
View Solution

