Through A, B and C lines RQ, PR and QP have been drawn, respectively parallel to sides BC, CA and AB of a ΔABC as shown in figure. Show that BC=12QR.
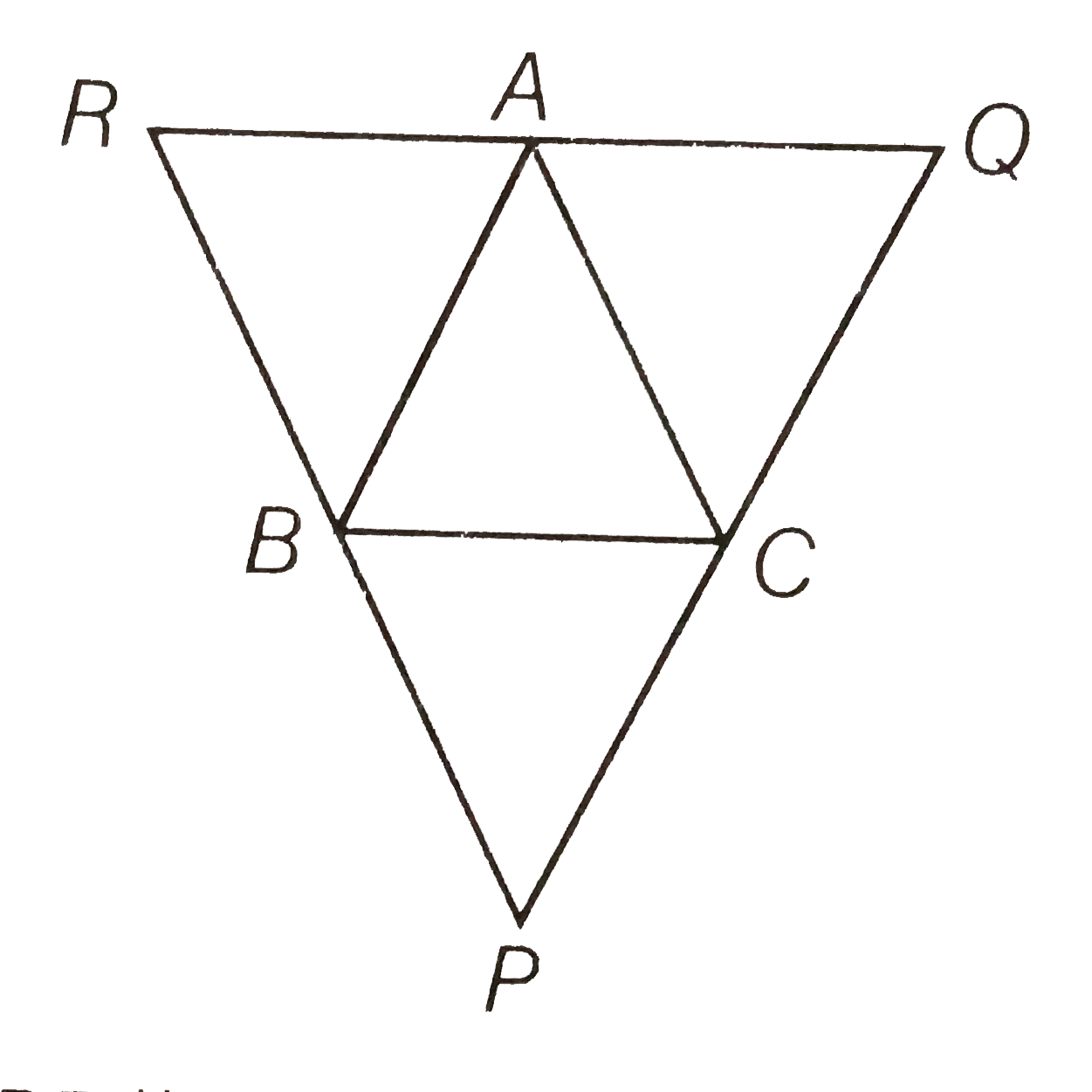
Given In ΔABC, PQ ∣∣ AB and PR ∣∣ AC and RQ ∣∣ BC.
To show BC=12QR
Proof In qudrilateral BCAR, BR||CAandBC||RA
So, quadrilateral, BCAR is a parallelogram.
∴ BC=AR ...(i)
Now, in quadrilateral BCQA, BC∣∣AQ
and AB∣∣QC
So, quadrilateral BCQA is a parallelogram,
∴ BC=AQ ...(ii)
On adding Eqs. (i) and (ii), we get
2BC=AR + AQ
⇒ 2BC=RQ
⇒ BC=12QR
Hence proved.
Topper's Solved these Questions
- QUADRILATERALS Book:NCERT EXEMPLAR ENGLISHChapter:QUADRILATERALS Exercise:LONG ANSWER TYPE QUESTIONS
Explore 18 Videos
- QUADRILATERALS Book:NCERT EXEMPLAR ENGLISHChapter:QUADRILATERALS Exercise:VERY SHORT ANSWER TYPE QUESTIONS
Explore 14 Videos
- POLYNOMIALSBook:NCERT EXEMPLAR ENGLISHChapter:POLYNOMIALSExercise:EXERCISE 2.4 Long Answer type Questions
Explore 9 Videos
- STATISTICS AND PROBABILITYBook:NCERT EXEMPLAR ENGLISHChapter:STATISTICS AND PROBABILITYExercise:LONG ANSWER TYPE QUESTIONS
Explore 12 Videos
Similar Questions
Given ABC , lines are drawn through A, B and C parallel respectively to the sides BC, CA and AB, forming triangle P Q R . Show that BC=1/2QR.
View SolutionIn the adjoining figure, ΔPQR is formed by the sides PQ, QR and RP which are drawn parallel to sides AB,BC and CA respectively of ΔABC. Prove that
PQ+QR+RP=2(AB+BC+CA).

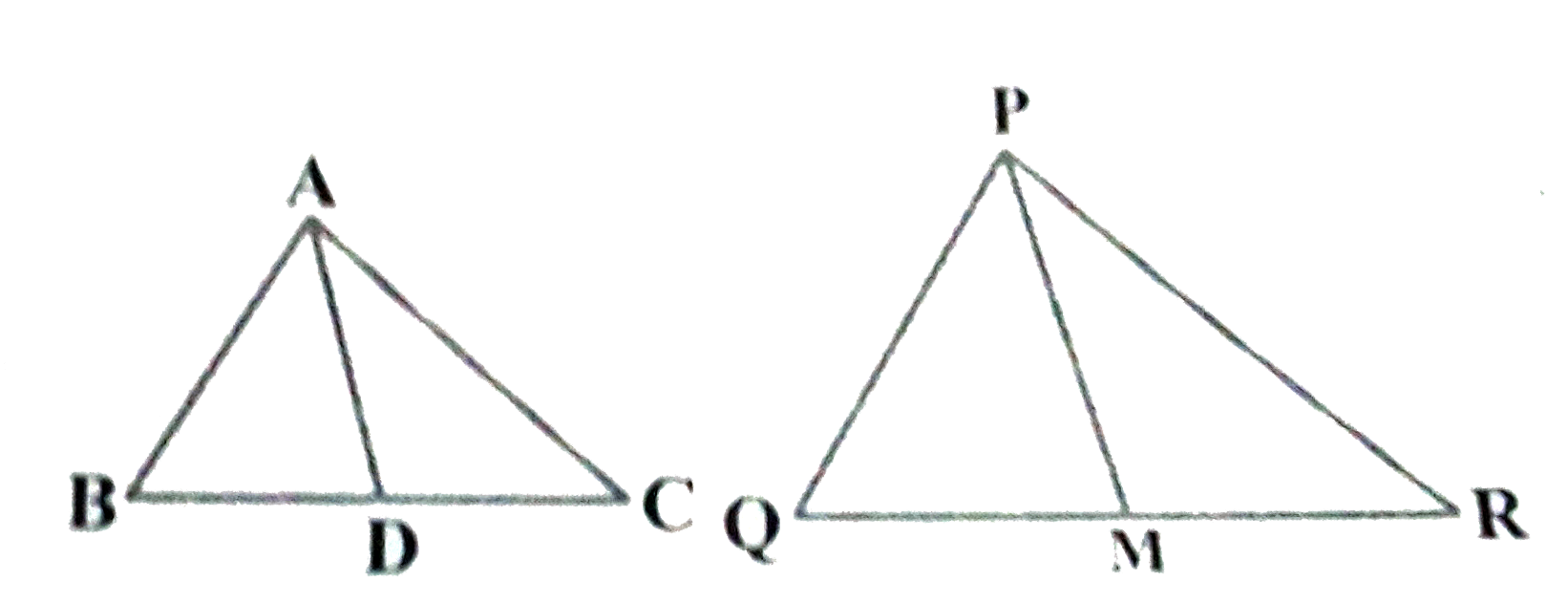
View SolutionSides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ΔPQR. Show that ΔABC~ΔPQR.
View SolutionIn triangle ABC, AB>AC and D is a point in side BC. Show that : AB>AD.
View SolutionIn triangle ABC, AB>AC and D is a point in side BC. Show that : AB>AD.
View SolutionTwo sides AB and BC and median AD of triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR. Show that:
ΔABD=ΔPQN
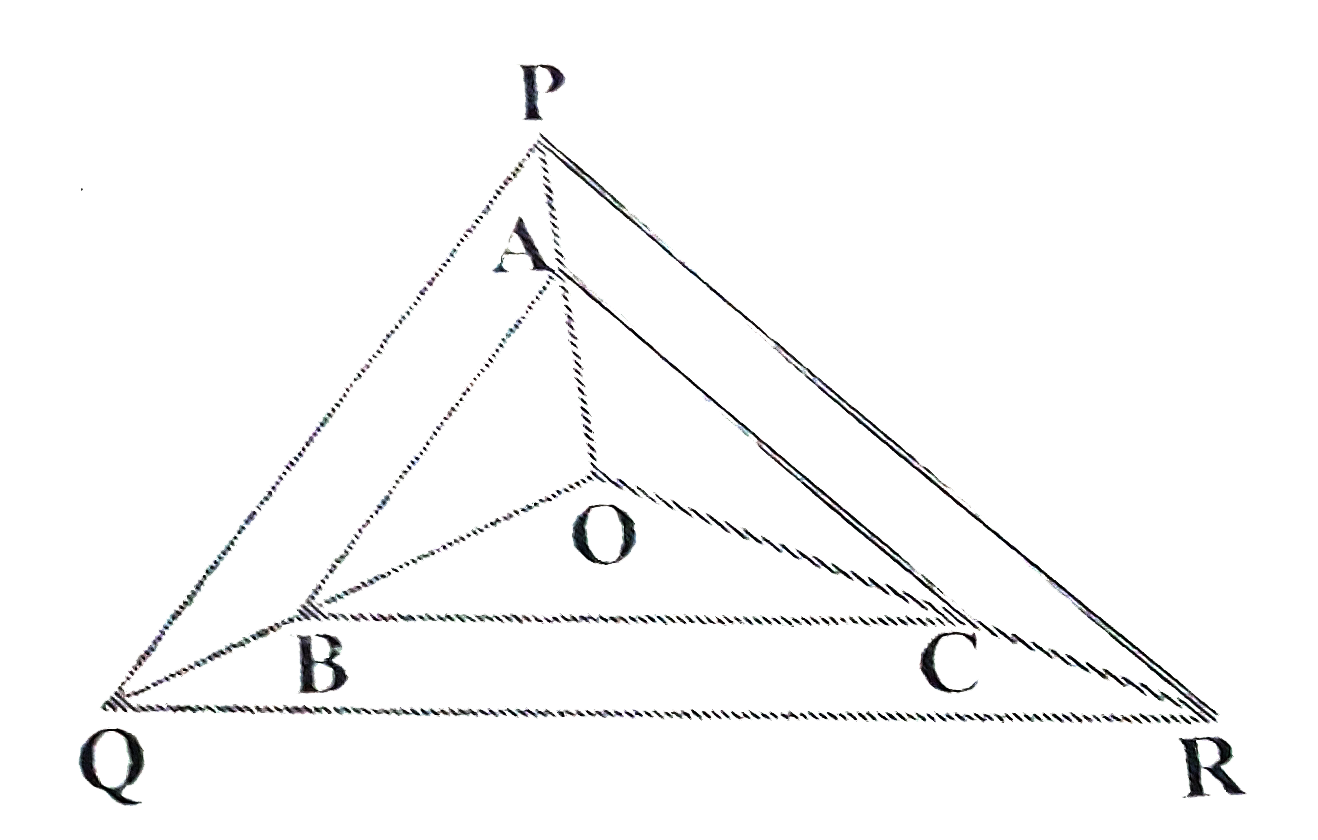
View SolutionIn figure A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.
View SolutionLet A, B, C respresent the vertices of a triangle, where A is the origin and B and C have position b and c respectively. Points M, N and P are taken on sides AB, BC and CA respectively, such that (AM)/(AB)=(BN)/(BC)=(CP)/(CA)=alpha Q. AN+BP+CM is
View SolutionLet →a,→b,→c represent respectively −−→BC,−−→CAand−−→AB where ABC is a triangle , Then ,
View SolutionLet the incircle of a ΔABC touches sides BC, CA and AB at D,E and F, respectively. Let area of ΔABC be Δ and thatof DEF be Δ'. If a, b and c are side of DetlaABC, then the value of abc(a+b+c)Δ'Δ3 is
View Solution