Points P and Q have been taken on opposite sides AB and CD, respectively of a parallelogram ABCD such that AP=CQ. Show that AC and PQ bisect each other.
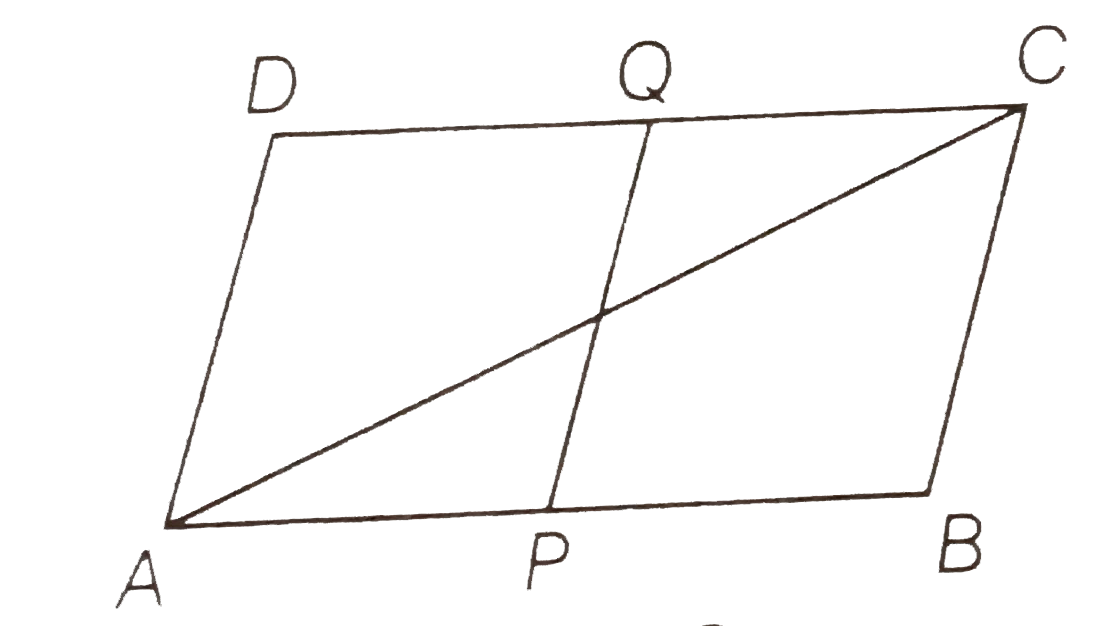
Given ABCD is a parallelogram and AP = CQ
To show AC and PQ bisect each each other.

Proof In ΔAMP and ΔCMQ,
∠MAP=∠MCQ [alternate interior angles]
AP=CQ [given]
and ∠APM=∠CQM [alternate interior angles]
∴ ΔAMP≅ΔCMQ [by ASA congruence rule]
⇒ AM=CM [by CPCT rule]
and PM=MQ [by CPCT rule]
Hence, AC and PQ bisect each other. Hence proved.
Topper's Solved these Questions
- QUADRILATERALS Book:NCERT EXEMPLAR ENGLISHChapter:QUADRILATERALS Exercise:LONG ANSWER TYPE QUESTIONS
Explore 18 Videos
- QUADRILATERALS Book:NCERT EXEMPLAR ENGLISHChapter:QUADRILATERALS Exercise:VERY SHORT ANSWER TYPE QUESTIONS
Explore 14 Videos
- POLYNOMIALSBook:NCERT EXEMPLAR ENGLISHChapter:POLYNOMIALSExercise:EXERCISE 2.4 Long Answer type Questions
Explore 9 Videos
- STATISTICS AND PROBABILITYBook:NCERT EXEMPLAR ENGLISHChapter:STATISTICS AND PROBABILITYExercise:LONG ANSWER TYPE QUESTIONS
Explore 12 Videos
Similar Questions
P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar (APB) = ar (BQC).
View SolutionL and M are the mid-points of sides AB and DC respectively of parallelogram ABCD. Prove that segments DL and BM trisect diagonal AC.
View SolutionP,Q,R are the points on the sides AB, BC and CA respectively of triangle ABC such that AP:PB=BQ:QC=AR:RC=1:2. Show that PBQR is a parallelogram.
View SolutionP and Q are points on opposite sides AD and BC of a parallelogram ABCD such that PQ passes through the point of intersection O of its diagonals AC and BD. Show that PQ is bisected at O.
View SolutionIf P and Q are the middle points of the sides BC and CD of the parallelogram ABCD, then AP+AQ is equal to
View SolutionP and Q are the mid-point of the opposite sides AB and CD of a parallelogram ABCD. AQ intersects DP at S and BQ intersects CP at R. Show that PQRS is a parallelogram.

View SolutionPQRS is a parallelogram. L and M are points on PQ and SR respectively such that PL = MR. Show that LM and QS bisect each other.
View SolutionP and Q are points on the sides AB and AC respectively of a △ABC. If AP= 2cm, PB = 4cm AQ= 3cm and QC= 6cm. Show that BC= 3PQ.
View SolutionX and Y are the mid-points of the opposite sides AB and DC of a parallelogram ABCD. Prove that □AXCY is a parallelogram.
View SolutionIn the diagram below, P and Q are midpoints of sides BC and AD respectively of the parallelogram ABCD. If side AB = diagonal BD: prove that the quadrilateral BPDQ is a rectangle.

View Solution