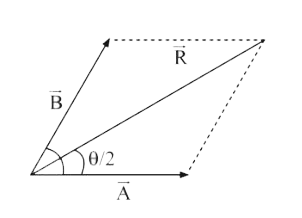
The angle between two vectors →A and →B is θ. The resultant of these vectors →R makes an angle of θ/2 with →A. which of the following is true?
A=2B
A=B2
A=B
AB=1
The correct Answer is:c
¯¯¯R is the angle bisectro
∴∣∣¯¯¯A∣∣=∣∣¯¯¯A∣∣
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - level 265videos
INTRODUCTION TO VECTORS & FORCES
- BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - JEE Main ( ARCHIVE ) ( LEVEL-1)12videos
INTRODUCTION TO VECTORS & FORCES
- BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - JEE Advanced ( ARCHIVE LEVEL-2)12videos
INTRODUCTION TO VECTORS & FORCES
- BOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive) TRUE/FALSE1videos
GRAVITATION
- BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN - 5EXERCISE - PART I : PHYSICS (SECTION - 2)5videos
JEE MAIN - 5
Similar Questions
The angle between two vector A and B is θ. Vector R is the resultant of the two vectors. If R makes an angle θ2 with A, then
View SolutionThe angle between Vectors (→A×→B) and (→B×→A) is
View SolutionWhat is the angle between the vector →A and →B as shown in figure ?
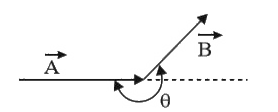 View Solution
View SolutionThe angle between the vector →A and →B is θ. Find the value of triple product →A.(→B×→A).
View SolutionThe angle between the vector →A and →B is θ. Find the value of triple product →A.(→B×→A).
View SolutionThe angle between the vector →A and →B is θ. Find the value of triple product →A.(→B×→A).
View SolutionThe angle between the vector →A and →B is θ. Find the value of triple product →A.(→B×→A).
View SolutionThe angle between vectors →Aand→B is 60∘ What is the ratio →A.→B and ∣∣→A×→B∣∣
View SolutionIf the angle between the vectors →a and →b is an acute angle, then the diffrence →a−→b is
View SolutionTwo vectors →Aand→B are at right angles to each other then
View Solution
