To get a resultant displacement of 10 m, two displacement vectors, one of magnitude 6 m another of 8 m should be combined :
parallel
anti-parallel
at an angle of
perpendicular to each other
The correct Answer is:d
To solve the problem of finding the correct configuration of two displacement vectors (6 m and 8 m) that results in a resultant displacement of 10 m, we will analyze each option step by step.
Step 1: Understand the vectors
We have two displacement vectors:
- →F1 with a magnitude of 6 m
- →F2 with a magnitude of 8 m
Step 2: Check the first option - Parallel
If the two vectors are parallel, the resultant displacement R is given by:
R=F1+F2=6m+8m=14m
Since we need a resultant of 10 m, this option is not valid.
Step 3: Check the second option - Anti-parallel
If the two vectors are anti-parallel, the resultant displacement R is given by:
R=F2−F1=8m−6m=2m
Again, since we need a resultant of 10 m, this option is also not valid.
Step 4: Check the third option - At an angle
If the two vectors are at an angle θ, the resultant displacement R can be calculated using the formula:
R=√F21+F22+2F1F2cos(θ)
However, we will analyze the fourth option before making a conclusion.
Step 5: Check the fourth option - Perpendicular
If the two vectors are perpendicular to each other, the resultant displacement R is given by:
R=√F21+F22=√62+82=√36+64=√100=10m
This matches our requirement of a resultant displacement of 10 m.
Conclusion
The correct configuration of the two displacement vectors (6 m and 8 m) that results in a resultant displacement of 10 m is when they are perpendicular to each other.
We have two displacement vectors:
- →F1 with a magnitude of 6 m
- →F2 with a magnitude of 8 m
If the two vectors are parallel, the resultant displacement R is given by:
R=F1+F2=6m+8m=14m
Since we need a resultant of 10 m, this option is not valid.
If the two vectors are anti-parallel, the resultant displacement R is given by:
R=F2−F1=8m−6m=2m
Again, since we need a resultant of 10 m, this option is also not valid.
If the two vectors are at an angle θ, the resultant displacement R can be calculated using the formula:
R=√F21+F22+2F1F2cos(θ)
However, we will analyze the fourth option before making a conclusion.
If the two vectors are perpendicular to each other, the resultant displacement R is given by:
R=√F21+F22=√62+82=√36+64=√100=10m
This matches our requirement of a resultant displacement of 10 m.
The correct configuration of the two displacement vectors (6 m and 8 m) that results in a resultant displacement of 10 m is when they are perpendicular to each other.
Topper's Solved these Questions
- INTRODUCTION TO VECTORS & FORCES BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - level 2
65 Videos
- INTRODUCTION TO VECTORS & FORCES BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - JEE Main ( ARCHIVE ) ( LEVEL-1)
12 Videos
- INTRODUCTION TO VECTORS & FORCES BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - JEE Advanced ( ARCHIVE LEVEL-2)
12 Videos
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive) TRUE/FALSE
1 Videos
- JEE MAIN - 5BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN - 5EXERCISE - PART I : PHYSICS (SECTION - 2)
5 Videos
Similar Questions
Represent graphically: A displacement of 20 m, north east.
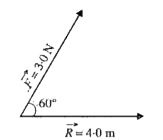
View SolutionThe vector →F is a force of 3.0 newton making an angle of 60∘ with the displacement . →R of magnitude 4.0 m , find
the magnitude and direction of the cross product →R×→F

View SolutionThe vector →F is a force of 3.0 newton making an angle of 60∘ with the displacement . →R of magnitude 4.0 m , find
the value of the dot product →F.→R
View SolutionA car makes a displacement of 100 m towards east and then 200 m towards north. Find the magnitude and direction of the resultant.
View SolutionA force of 25 N causes a displacement of 4 m in its own direction. What is the magnitude of work done ?
View SolutionThe magnetitude of pairs of displacement vectors are given. Which pairs of displacement vector cannot be added to give a resultant vector of magnitude 13 cm?
View SolutionThe resultant of two vectors is perpendicular to first vector of magnitude 6N. If the resultant has magnitude 6√3N, then magnitude of second vector is
View SolutionRepresent graphically: A displacement of 50 m, 600 south of east
View SolutionA bird moves in such a way that it has a displacement of 12 m towards east, 5 m towards north and 9 m vertically upwards. Find the magnitude of its displacement.
View SolutionThe SI unit of distance is m, whereas the SI unit of displacement is km.
View Solution
