Question

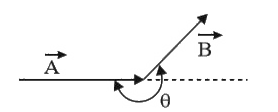
If the angle between the vectors $\overrightarrow{a}$ and $\overrightarrow{b}$ is an acute angle, then the diffrence $\overrightarrow{a}-\overrightarrow{b}$ is

Options

A. The major diagonal of the parallelogram
B. The minor diagnol of the parallelogram
C. Any of the above
D. None of the above

Answer

B

Explanation

To solve the problem, we need to analyze the vectors $$\overrightarrow{a}$$ and $$\overrightarrow{b}$$ and their relationship when the angle between them is acute. Here’s a step-by-step solution:

Step 1: Understand the Vectors
We have two vectors, \(\vec{a}\) and \(\vec{b}\), with an acute angle \(\theta\) between them. An acute angle means \(0 < \theta < 90^\circ\).

Hint: Remember that an acute angle is less than 90 degrees.

Step 2: Visualize the Vectors
Draw the vectors \(\vec{a}\) and \(\vec{b}\) originating from the same point. Since the angle is acute, \(\vec{b}\) will be positioned such that it is within the first quadrant relative to \(\vec{a}\).

Hint: Sketch the vectors on a coordinate plane to visualize their positions.

Step 3: Construct the Parallelogram
To find \(\vec{a} - \vec{b}\), we can use the parallelogram law. Draw \(\vec{b}\) in the opposite direction to get \(-\vec{b}\). Now, you can form a parallelogram with \(\vec{a}\) and \(-\vec{b}\).

Hint: The diagonal of the parallelogram formed by \(\vec{a}\) and \(-\vec{b}\) represents the vector \(\vec{a} - \vec{b}\).

Step 4: Analyze the Resulting Vector
The diagonal that represents \(\vec{a} - \vec{b}\) will be the minor diagonal of the parallelogram. Since \(\vec{a}\) is longer than \(\vec{b}\) (as the angle is acute), \(\vec{a} - \vec{b}\) will also point in the same general direction as \(\vec{a}\).

Hint: The direction of \(\vec{a} - \vec{b}\) will be similar to that of \(\vec{a}\) because \(\vec{a}\) is greater than \(\vec{b}\).

Step 5: Conclusion
Since \(\vec{a}\) is greater than \(\vec{b}\) and the angle between them is acute, the resultant vector \(\vec{a} - \vec{b}\) will also be a vector pointing in the same direction as \(\vec{a}\) but with a smaller magnitude than \(\vec{a}\).

Final Answer: The difference \(\vec{a} - \vec{b}\) is a vector that points in the same direction as \(\vec{a}\) and has a magnitude less than that of \(\vec{a}\).