Question

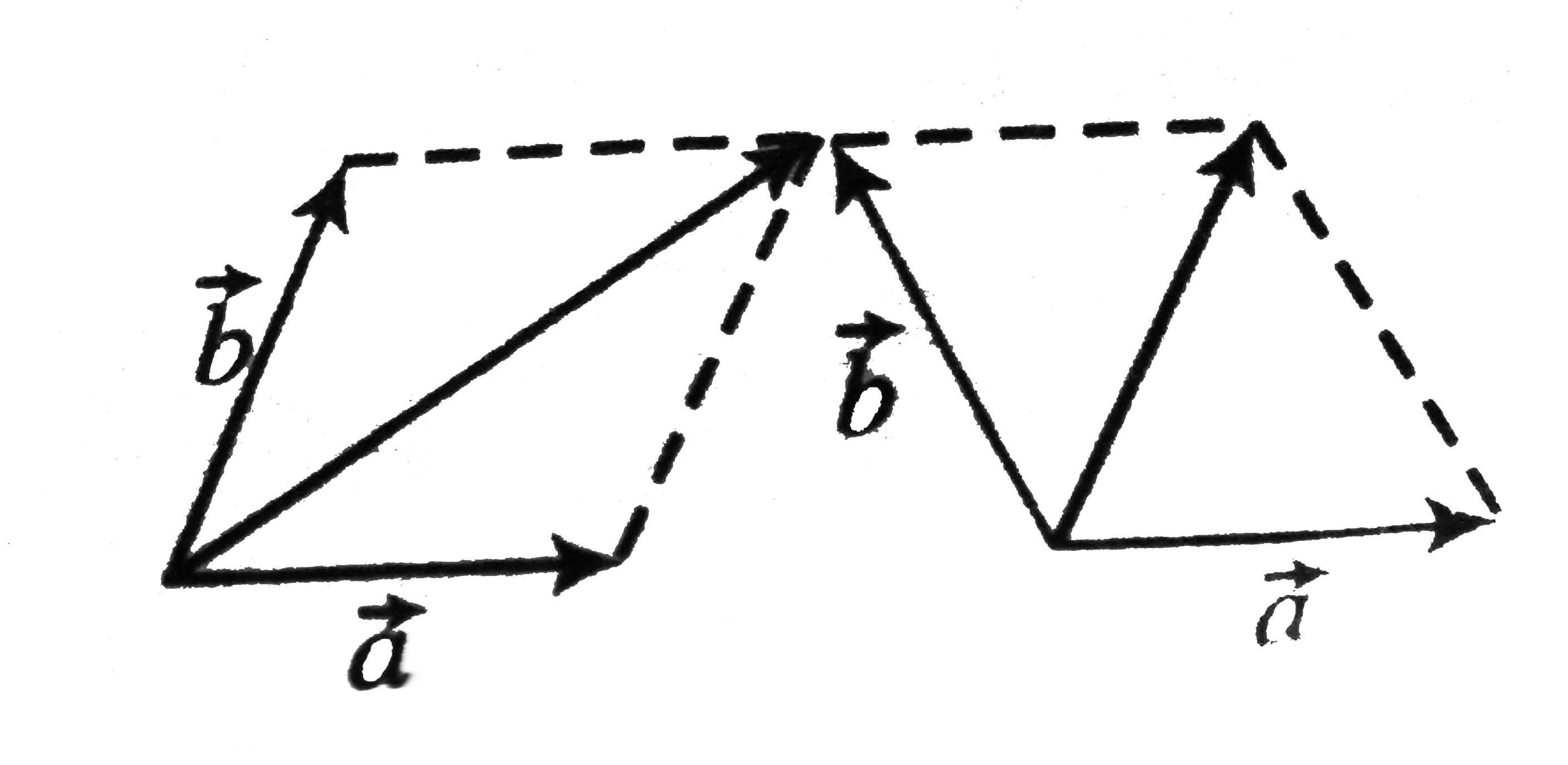
If a parallelogram is formed with two sides represented by vector $\overrightarrow{a}$ and $\overrightarrow{b}$, then $\overrightarrow{a}+\overrightarrow{b}$ represents the

Options

A. Major diagonal when the angle between vectors is acute
B. Minor diagonal when the angle between vector is obtuse
C. Both of the above
D. None of the above

Answer

C

Explanation

To solve the problem, we need to analyze the properties of vectors and how they relate to the geometry of a parallelogram.

1. Understanding the Vectors:
- We are given two vectors, \( \vec{a} \) and \( \vec{b} \), which represent two adjacent sides of a parallelogram.

2. Visualizing the Parallelogram:
- When we draw the vectors \( \vec{a} \) and \( \vec{b} \) from a common point, they form a parallelogram where:
- One vertex is at the origin (where both vectors start).
- The opposite vertex is reached by moving along \( \vec{a} \) and then along \( \vec{b} \).

3. Identifying the Diagonals:
- In a parallelogram, there are two diagonals:
- One diagonal connects the origin to the vertex opposite to the one reached by \( \vec{a} \) and \( \vec{b} \).
- The other diagonal connects the endpoints of \( \vec{a} \) and \( \vec{b} \).

4. Calculating the Major Diagonal:
- The major diagonal of the parallelogram is represented by the vector sum \( \vec{a} + \vec{b} \). This diagonal stretches from the origin to the point reached by moving along both vectors.

5. Calculating the Minor Diagonal:
- The minor diagonal can be represented by the vector \( \vec{b} - \vec{a} \). This diagonal connects the endpoints of the two vectors.

6. Conclusion:
- Therefore, the vector \( \vec{a} + \vec{b} \) represents the major diagonal of the parallelogram formed by the vectors \( \vec{a} \) and \( \vec{b} \).

Final Answer:
\( \vec{a} + \vec{b} \) represents the major diagonal of the parallelogram formed by the vectors \( \vec{a} \) and \( \vec{b} \).

---