The resultant of two vectors →P and →Q is →R. If →Q is doubled then the new resultant vector is perpendicular to →P. Then magnitude of →R is :-
P+Q
P
P−Q
Q
The correct Answer is:D
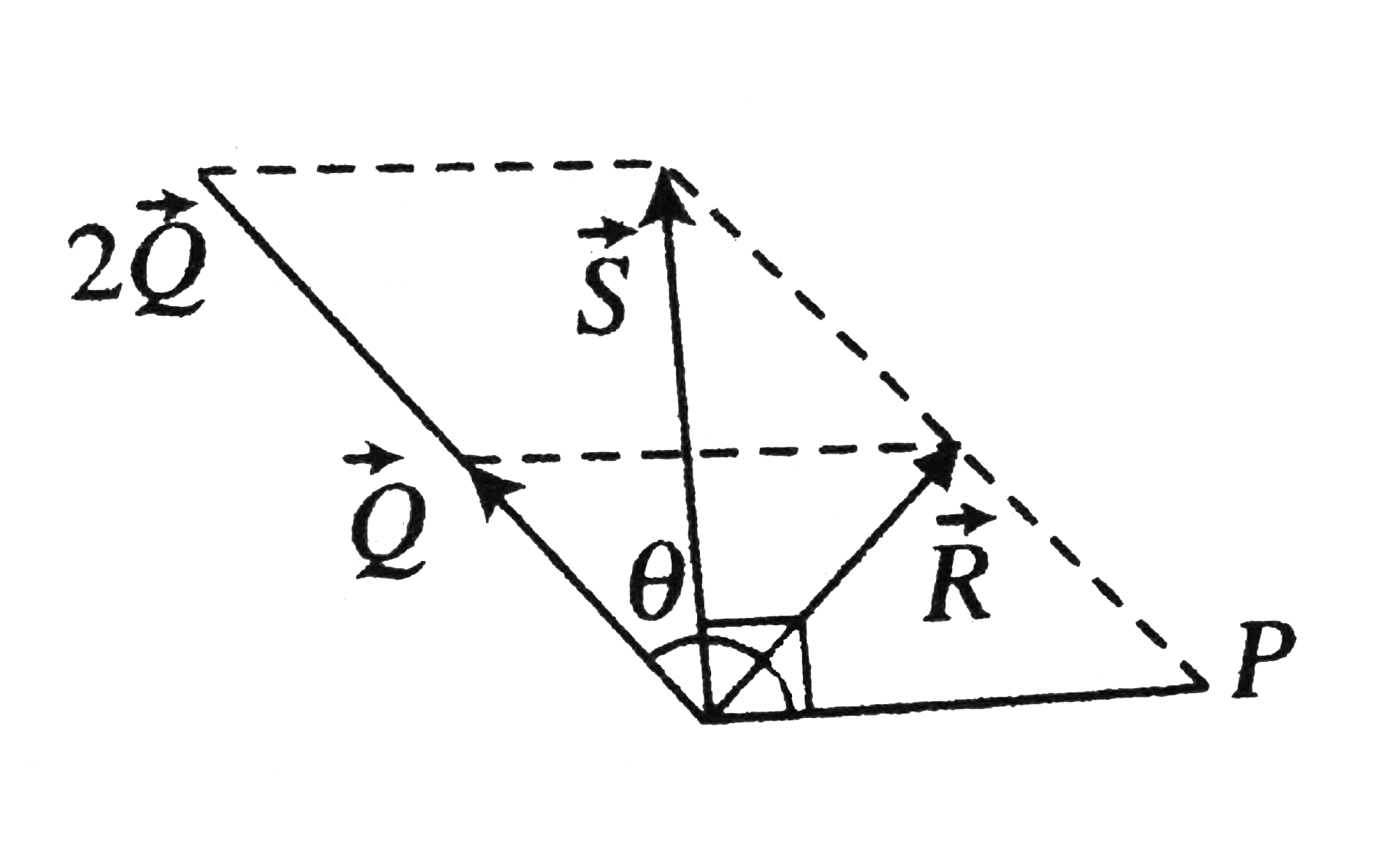
tan90∘=2QsinθP+2Qcosθ⇒∞=2QsinθP+2Qcosθ
⇒P+2Qcosθ=0
Now R2=P2+Q2+2PQcosθ
Q2+P[P+2Qcosθ]
R2=Q2⇒R=Q
Alternative method:
→R=→P+→Q⇒→P=→R−→Q
and →S=→P+2→Q=→R−→Q+2→Q=→R+→Q
Now, →S and →P are perpendicular(figure), So
→S.→P=0⇒(→R+→Q).(→R−→Q)=0
⇒→R=Q2⇒R=Q
Topper's Solved these Questions
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise Subjective
Explore 28 Videos
- TRAVELLING WAVESBook:CENGAGE PHYSICS ENGLISHChapter:TRAVELLING WAVESExercise:Integer
Explore 9 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Archives (integer)
Explore 4 Videos
Similar Questions
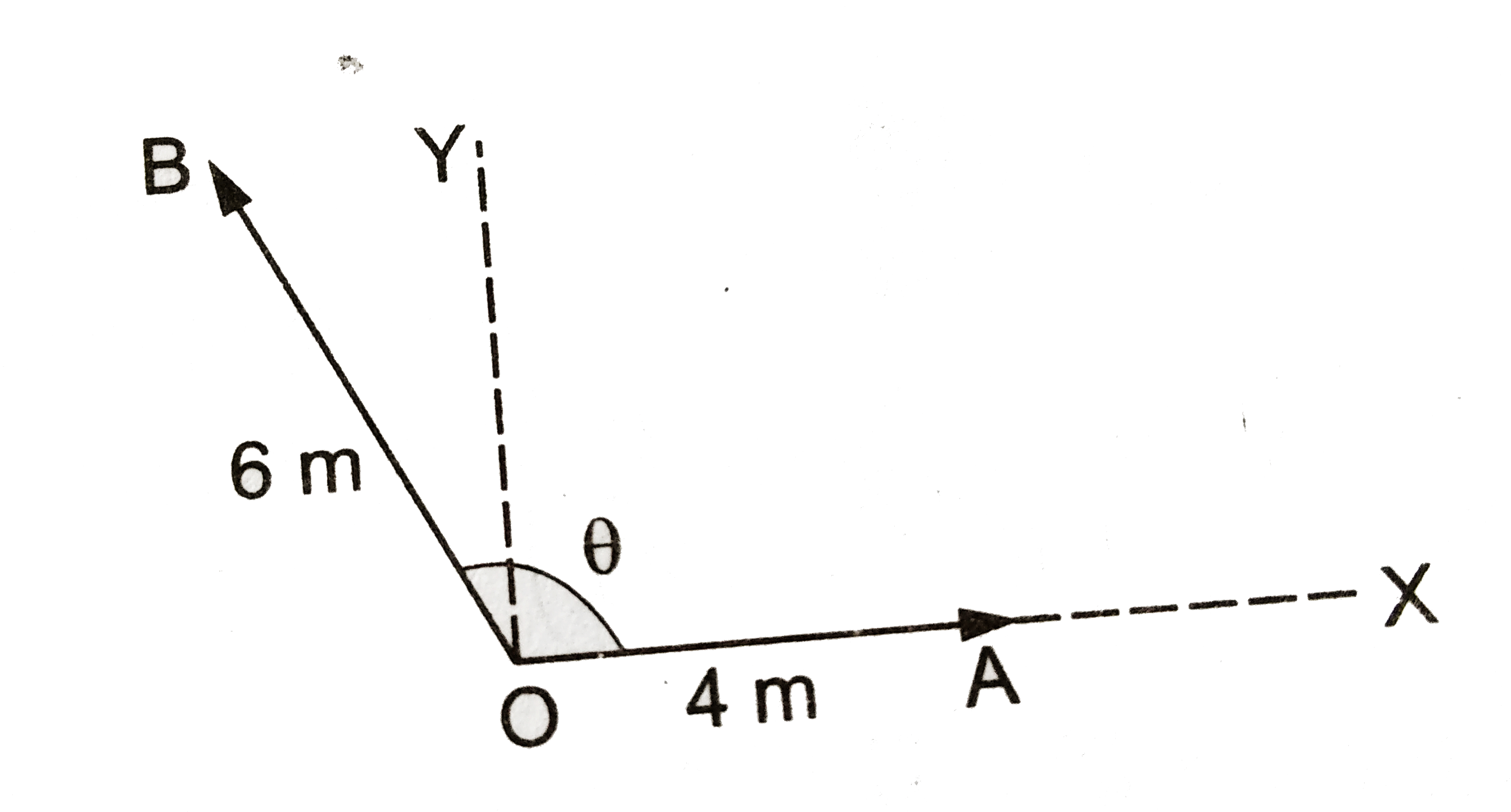
The resultant of vectors −−→OAand−−→OB is perpendicular to −−→OA. Find the angle AOB.
View SolutionThe resultant of →P and →Q is →R. If →Q is doubled, →R is doubled, when →Q is reversed, →R is again doubled. Find P:Q:R.
View SolutionThe resultant and dot product of two vectors →aand→b is equal to the magnitude of →a. Show that when the vector →a is doubled , the new resultant is perpendicular to →b .
View SolutionIf →aand→b are two vector such that ∣∣→a+→b∣∣=|→a|, then show that vector |2a+b| is perpendicular to →b.
View SolutionThe resultant vector of →P and →Q is →R. On reversing the direction of →Q the resultant vector becomes →S. Show that R2+S2=2(P2+Q2)
View SolutionThe resultant →Pand→Q is perpendicular to →P. What is the angle between →Pand→Q?
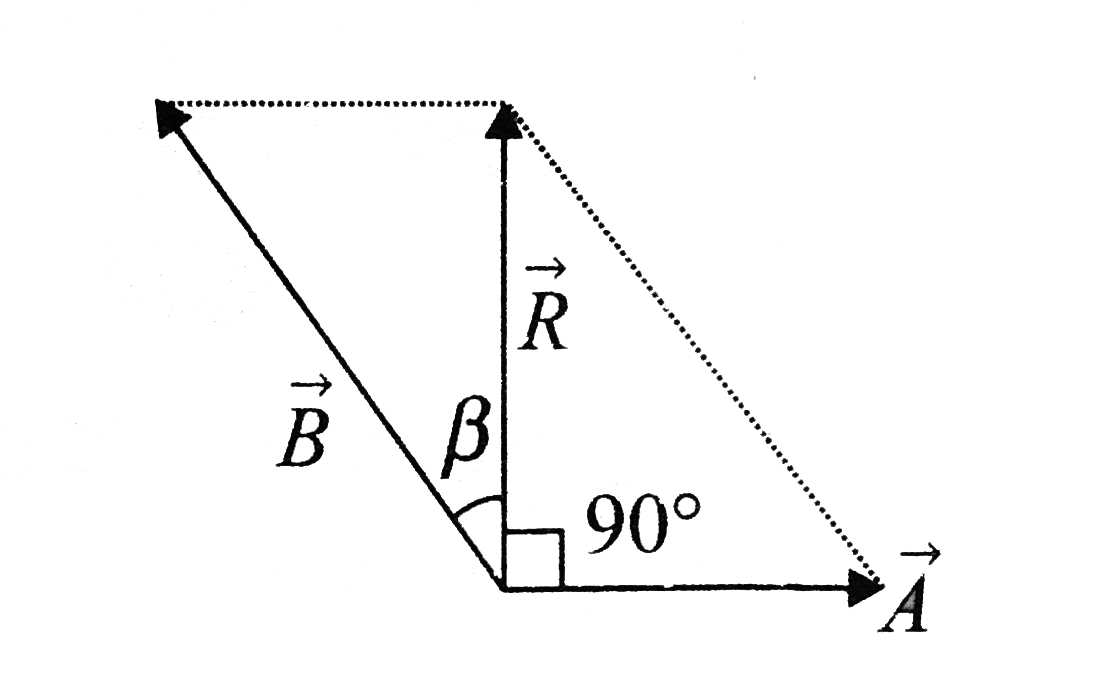
View SolutionThe resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitudes is equal to half of the magnitudes of vector →B (figure). The angle between →A and →B is
View SolutionIf ∣∣→P+→Q∣∣=∣∣→P−→Q∣∣ , find the angle between →P and →Q.
View SolutionIf →a,→b are two vectors such that ∣∣→a+→b∣∣=∣∣→b∣∣, then prove that →a+2→b is perpendicular to →a .
View SolutionIf two vectors →aand→b are such that ∣∣→a.→b∣∣=∣∣→a×→b∣∣, then find the angle the vectors →aand→b
View Solution