The de Broglie wavelenght (λ) associated with a photoelectron varies with the frequency (v) of the incident radiation as,[v0 is threshold frequency]:
λ∝1(v−v0)32
λ∝1(v−v0)14
∝1(v−v0)12
λ∝1(v−v0)
The correct Answer is:C
To solve the problem regarding the de Broglie wavelength (λ) associated with a photoelectron in relation to the frequency (ν) of the incident radiation, we can follow these steps:
1. Understand the Photoelectric Effect:
The photoelectric effect states that when light of sufficient frequency (ν) strikes a material, it can eject electrons. The energy of the incident photons is given by the equation:
E=hν
where h is Planck's constant.
2. Define the Threshold Frequency:
The threshold frequency (ν₀) is the minimum frequency required to eject an electron from the material. The energy corresponding to this frequency is:
E0=hν0
3. Energy Conservation:
The total energy of the incident photon is used to overcome the work function (φ) of the material and to provide kinetic energy (KE) to the ejected electron:
hν=φ+KE
where KE=12mv2 (m is the mass of the electron and v is its velocity).
4. Express Kinetic Energy:
Rearranging the energy equation gives:
KE=hν−hν0
Substituting for KE:
12mv2=hν−hν0
5. Solve for Velocity (v):
From the above equation, we can express the velocity (v) of the photoelectron:
v=√2(hν−hν0)m
6. Relate Velocity to de Broglie Wavelength:
The de Broglie wavelength (λ) is given by:
λ=hp
where p is the momentum. The momentum p can be expressed as:
p=mv
Therefore, substituting for v:
λ=hmv
7. Substitute for v:
Substituting the expression for v into the equation for λ:
λ=hm√2(hν−hν0)m
Simplifying this gives:
λ=h√m√2(hν−hν0)
This can be rewritten as:
λ∝1√hν−hν0
8. Final Expression:
Since hν−hν0=h(ν−ν0), we can express the relationship as:
λ∝1√ν−ν0
Thus, the de Broglie wavelength (λ) is inversely proportional to the square root of the difference between the frequency of the incident radiation and the threshold frequency.
Conclusion:
The correct relationship is:
λ∝1√ν−ν0
Thus, the answer is option C, which indicates that the de Broglie wavelength is inversely proportional to the square root of ν−ν0.
The photoelectric effect states that when light of sufficient frequency (ν) strikes a material, it can eject electrons. The energy of the incident photons is given by the equation:
E=hν
where h is Planck's constant.
The threshold frequency (ν₀) is the minimum frequency required to eject an electron from the material. The energy corresponding to this frequency is:
E0=hν0
The total energy of the incident photon is used to overcome the work function (φ) of the material and to provide kinetic energy (KE) to the ejected electron:
hν=φ+KE
where KE=12mv2 (m is the mass of the electron and v is its velocity).
Rearranging the energy equation gives:
KE=hν−hν0
Substituting for KE:
12mv2=hν−hν0
From the above equation, we can express the velocity (v) of the photoelectron:
v=√2(hν−hν0)m
The de Broglie wavelength (λ) is given by:
λ=hp
where p is the momentum. The momentum p can be expressed as:
p=mv
Therefore, substituting for v:
λ=hmv
Substituting the expression for v into the equation for λ:
λ=hm√2(hν−hν0)m
Simplifying this gives:
λ=h√m√2(hν−hν0)
This can be rewritten as:
λ∝1√hν−hν0
Since hν−hν0=h(ν−ν0), we can express the relationship as:
λ∝1√ν−ν0
Thus, the de Broglie wavelength (λ) is inversely proportional to the square root of the difference between the frequency of the incident radiation and the threshold frequency.
The correct relationship is:
λ∝1√ν−ν0
Thus, the answer is option C, which indicates that the de Broglie wavelength is inversely proportional to the square root of ν−ν0.
Topper's Solved these Questions
- ATOMIC STRUCTUREBOOK - VMC MODULES ENGLISHCHAPTER - ATOMIC STRUCTUREEXERCISE - JEE Advanced (Archive )
67 Videos
- ATOMIC STRUCTUREBOOK - VMC MODULES ENGLISHCHAPTER - ATOMIC STRUCTUREEXERCISE - LEVEL - 2 ( Numerical value type for JEE Main )
16 Videos
- AMINESBOOK - VMC MODULES ENGLISHCHAPTER - AMINESEXERCISE - IN CHAPTER EXERCISE H
10 Videos
- CHEMICAL BONDING & CHEMICAL STRUCTURE BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL BONDING & CHEMICAL STRUCTURE EXERCISE - IMPECCABLE
50 Videos
Similar Questions
Maximum kinetic energy (Ek) of a photoelectron varies with the frequency (v) of the incident radiation as
View SolutionDe Broglie wavelength λ associated with neutrons is related with absolute temperature T as
View SolutionThe de - Broglie wavelength associated with the particle of mass m moving with velocity v is
View SolutionCalculate de Broglie wavelength associated with an electron, accelerated through a potential difference of 400V.
View SolutionIn an experiment of photo-electric effect, the graph of maximum kinetic energy Ek of the emitted photoelectrons versus the frequency v of the incident light is a straight line AB as shown in figure below :

Threshold frequency of the metal.
View SolutionThe group velocity of the de Broglie wave packet associated with a particle moving with velocity v is-
View SolutionIn an experiment of photoelectric effect, the graph of maximum kinetic energy EK of the emitted photoelectrons versus the frequency v of the incident light is a straight line AB as shown in Figure below:
Find : (i) Threshold frequency of the metal.
(ii) work function of the metal
(iii) Stopping potential for the photoelectrons emitted by the light of frequency v=30×1014 Hz.
View Solution(i) Plot a labelled graph of |Vs| where Vs is stopping potential versus frequency f of the incident radiation.
(ii) State how will you use this graph to determine the value of Planck.s constant.
View SolutionIn an experiment of photo-electric effect, the graph of maximum kinetic energy Ek of the emitted photoelectrons versus the frequency v of the incident light is a straight line AB as shown in figure below :
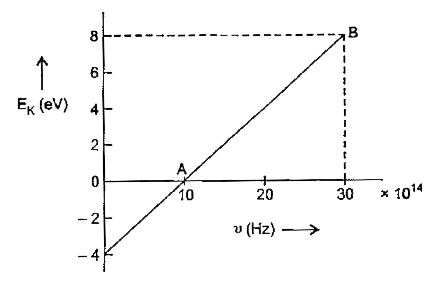
Stopping potential for the photoelectrons emitted by the light of frequency
v=30×1014Hz
View SolutionExplain giving reasons for the following :
(a) Photoelectric current in a photocell increases with the increase in intensity of the incident radiation.
(b) The stopping potential V0 varies linearly with the frequency ν of the incident radiation for a given photosensitive surface with the slope remaining the same for different surfaces.
(c) Maximum kinetic energy of the photoelectrons is independent of the intensity of incident radiation.
View Solution
