Ejection of the photoelectron from metal in the photoelectric effect experiment can be stopped by applying 0.5 V when the radiation of 250 nm is used. The work function of the metal is
5 eV
4 eV
5.5 eV
4.5 eV
The correct Answer is:D
To find the work function (φ) of the metal in the photoelectric effect experiment, we can use the following steps:
Step 1: Understand the relationship between energy, work function, and kinetic energy
The energy of the incoming photon (E) can be expressed as:
E=ϕ+KE
Where:
- E is the energy of the photon,
- ϕ is the work function of the metal,
- KE is the kinetic energy of the ejected electron.
Step 2: Calculate the energy of the photon
The energy of the photon can be calculated using the formula:
E=hcλ
Where:
- h is Planck's constant (6.626×10−34J s),
- c is the speed of light (3×108m/s),
- λ is the wavelength of the radiation (in meters).
Given that the wavelength λ=250nm=250×10−9m, we can substitute the values into the equation.
Step 3: Substitute the values into the energy equation
Substituting the values into the energy equation:
E=(6.626×10−34J s)(3×108m/s)250×10−9m
Step 4: Calculate the energy in joules
Calculating this gives:
E=(6.626×10−34)(3×108)250×10−9
E=1.9878×10−25250×10−9
E=7.9512×10−19J
Step 5: Convert energy from joules to electron volts
To convert joules to electron volts, we use the conversion factor 1eV=1.6×10−19J:
E=7.9512×10−191.6×10−19≈4.969eV
Step 6: Use the stopping potential to find kinetic energy
The stopping potential Vs is given as 0.5 V, which is equivalent to 0.5 eV. The kinetic energy of the ejected electron can be expressed as:
KE=eVs=0.5eV
Step 7: Substitute into the energy equation
Now, substituting the values into the energy equation:
4.969eV=ϕ+0.5eV
Step 8: Solve for the work function
Rearranging the equation to solve for φ:
ϕ=4.969eV−0.5eV
ϕ=4.469eV
Step 9: Round to the appropriate significant figures
Rounding this to one decimal place gives:
ϕ≈4.5eV
Final Answer
The work function of the metal is approximately 4.5 eV.
---
The energy of the incoming photon (E) can be expressed as:
E=ϕ+KE
Where:
- E is the energy of the photon,
- ϕ is the work function of the metal,
- KE is the kinetic energy of the ejected electron.
The energy of the photon can be calculated using the formula:
E=hcλ
Where:
- h is Planck's constant (6.626×10−34J s),
- c is the speed of light (3×108m/s),
- λ is the wavelength of the radiation (in meters).
Substituting the values into the energy equation:
E=(6.626×10−34J s)(3×108m/s)250×10−9m
Calculating this gives:
E=(6.626×10−34)(3×108)250×10−9
E=1.9878×10−25250×10−9
E=7.9512×10−19J
To convert joules to electron volts, we use the conversion factor 1eV=1.6×10−19J:
E=7.9512×10−191.6×10−19≈4.969eV
The stopping potential Vs is given as 0.5 V, which is equivalent to 0.5 eV. The kinetic energy of the ejected electron can be expressed as:
KE=eVs=0.5eV
Now, substituting the values into the energy equation:
4.969eV=ϕ+0.5eV
Rearranging the equation to solve for φ:
ϕ=4.969eV−0.5eV
ϕ=4.469eV
Rounding this to one decimal place gives:
ϕ≈4.5eV
The work function of the metal is approximately 4.5 eV.
Topper's Solved these Questions
- ATOMIC STRUCTUREBook:VMC MODULES ENGLISHChapter:ATOMIC STRUCTUREExercise:JEE Advanced (Archive )
Explore 67 Videos
- ATOMIC STRUCTUREBook:VMC MODULES ENGLISHChapter:ATOMIC STRUCTUREExercise:LEVEL - 2 ( Numerical value type for JEE Main )
Explore 16 Videos
- AMINESBook:VMC MODULES ENGLISHChapter:AMINESExercise:IN CHAPTER EXERCISE H
Explore 10 Videos
- CHEMICAL BONDING & CHEMICAL STRUCTURE Book:VMC MODULES ENGLISHChapter:CHEMICAL BONDING & CHEMICAL STRUCTURE Exercise:IMPECCABLE
Explore 50 Videos
Similar Questions
The ejection of the photoelectron from the silver metal in the photoelectric effect experiment can be stopped by applying the voltage of 0.35V when the radiation 256.7nm is used. Calculate the work function for silver metal.
View SolutionThe ejection of the photoelectron from the silver metal in the photoelectric effect experiment can be stopped by applying the voltage of 0.35 V when the radiation 256.7 nm is used, Calculate the work function for silver metal.
View SolutionEnergy required to stop the ejection of electrons from certain metal plate was found to be 0.2 eV when an electromagnetic radiation of 330 nm was made to fall on it the work function of the metal is
View SolutionIn photoelectric effect the work function of a metal is 3.5 eV. The emitted electrons can be stopped by applying a potential of –1.2 V. Then
View SolutionIn the photoelectric effect, the maximum speed of electrons is found to be 6×105ms−1. The wavelength used is 4000Å. The work function of the metal is
View SolutionThe kinetic energy of the most energetic photoelectrons emitted from a metal surface is doubled when the wavelength of the incident radiation is reduced from λ1 to λ2 The work function of the metal is
View SolutionElectrons in hydrogen like atom (Z=3) make transition from the fifth to the fourth orbit and from the third orbit. The resulting radiation are incident normally on a metal plate and eject photoelectrons. The stopping potential for the photoelectrons ejected by the shorter wavelength is 3.95 volts. Calculate the work function of the metal and the stopping potential for the photoelectron ejected by longer wavelength
(Rydberg constant=1.094×107m−1
View SolutionThe kinetic energy of most energetic electrons emitted from a metallic surface is doubled when the wavelength λ of the incident radiation is changed from 400 nm to 310 nm. The work function of the metal is
View Solution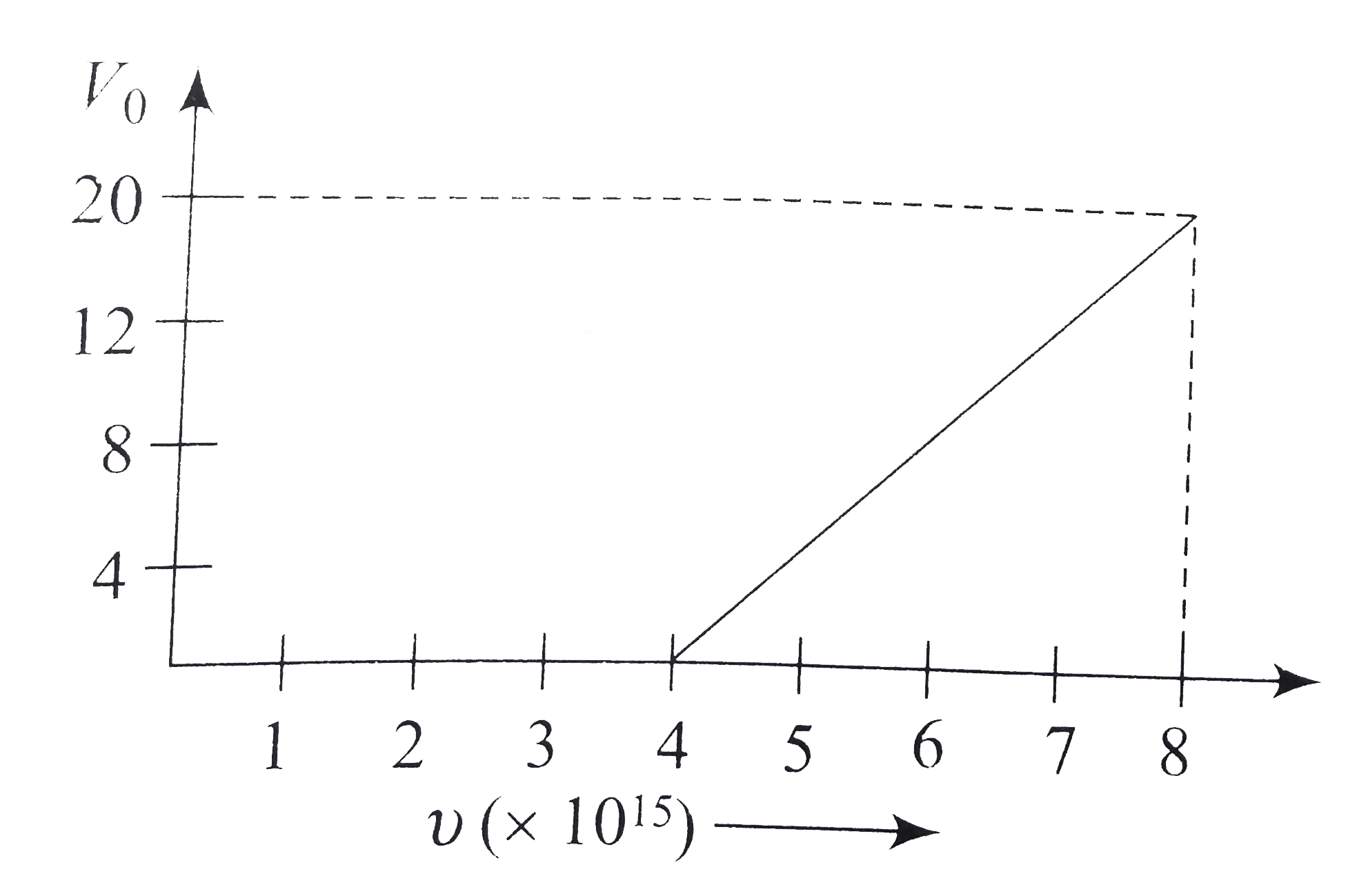
When a high frequency electromagnetic radiation is incident on a metallic surface, electrons are emitted from the surface. Energy of emitted photoelectrons depends only on the frequency of incident electromagnetic radiation and the number of emitted electrons depends only on the intensity of incident light.
Einstein's protoelectron equation [Kmax=hv−ϕ] correctly ecplains the PE, where υ= frequency of incident light and ϕ= work function.
Q. For photoelectric effect in a metal, the graph of the stopping potential V0 (in volt) versus frequency υ (in hertz) of the incident radiation is shown in Fig. The work function of the metal (in eV) is.
View SolutionWhen the energy of the incident radiation is increased by 20% , kinetic energy of the photoelectrons emitted from a metal surface increased from 0.5eV→0.8eV. The work function of the metal is
View Solution

