State True or False :
The Graphical solution set of the inequation 0≤y,x≥0
lies in second quadrant.
The correct Answer is:False
To determine whether the statement is true or false, we need to analyze the given inequations: 0≤y and x≥0.
1. Understanding the Inequations:
- The inequation 0≤y indicates that y must be greater than or equal to 0. This means that the values of y can be 0 or any positive number.
- The inequation x≥0 indicates that x must be greater than or equal to 0. This means that the values of x can be 0 or any positive number.
2. Identifying the Quadrants:
- In the Cartesian coordinate system, the quadrants are defined as follows:
- First Quadrant: x>0 and y>0
- Second Quadrant: x<0 and y>0
- Third Quadrant: x<0 and y<0
- Fourth Quadrant: x>0 and y<0
3. Finding the Graphical Solution Set:
- Since both x and y are non-negative (i.e., x≥0 and y≥0), the solution set will only include points in the first quadrant and along the axes where x and y are both non-negative.
- Specifically, this includes the points where x=0 (the y-axis) and y=0 (the x-axis), as well as all points in the first quadrant where both x and y are positive.
4. Conclusion:
- The graphical solution set of the inequations 0≤y and x≥0 does not lie in the second quadrant. Instead, it lies in the first quadrant and along the axes.
- Therefore, the statement "The Graphical solution set of the inequation 0≤y,x≥0 lies in the second quadrant" is False.
Final Answer:
False
- The inequation 0≤y indicates that y must be greater than or equal to 0. This means that the values of y can be 0 or any positive number.
- The inequation x≥0 indicates that x must be greater than or equal to 0. This means that the values of x can be 0 or any positive number.
- In the Cartesian coordinate system, the quadrants are defined as follows:
- First Quadrant: x>0 and y>0
- Second Quadrant: x<0 and y>0
- Third Quadrant: x<0 and y<0
- Fourth Quadrant: x>0 and y<0
- Since both x and y are non-negative (i.e., x≥0 and y≥0), the solution set will only include points in the first quadrant and along the axes where x and y are both non-negative.
- Specifically, this includes the points where x=0 (the y-axis) and y=0 (the x-axis), as well as all points in the first quadrant where both x and y are positive.
- The graphical solution set of the inequations 0≤y and x≥0 does not lie in the second quadrant. Instead, it lies in the first quadrant and along the axes.
- Therefore, the statement "The Graphical solution set of the inequation 0≤y,x≥0 lies in the second quadrant" is False.
False
Topper's Solved these Questions
- QUESTION BANK 2021Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:QUESTION BANK 2021Exercise:Part II LINEAR PROGRAMMING PROBLEMS (C. Fill in each of the following blanks)
Explore 12 Videos
- QUESTION BANK 2021Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:QUESTION BANK 2021Exercise:Part II LINEAR PROGRAMMING PROBLEMS (D. Solve the following problems)
Explore 12 Videos
- QUESTION BANK 2021Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:QUESTION BANK 2021Exercise:Part II LINEAR PROGRAMMING PROBLEMS (1. Select the most appropriate option for each of the following. )
Explore 12 Videos
- PROBABILITY DISTRIBUTIONBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:PROBABILITY DISTRIBUTIONExercise:MULTIPLE CHOICE QUESTIONS
Explore 9 Videos
- THREE DIMENSIONAL GEOMETRY Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:THREE DIMENSIONAL GEOMETRY Exercise:MULTIPLE CHOICE QUESTIONS
Explore 8 Videos
Similar Questions
Knowledge Check
Solution set of inequation x≥0 is
AHalf-plane on the left of y-axisBHalf-plane on the right of y-axis excluding the points on y-axisCHalf-plane on the right of y-axis including the points on y-axisDNone of theseThe graphical solution of 3x−6≥0 is
A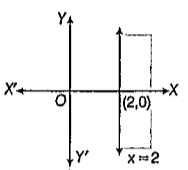 B
B C
C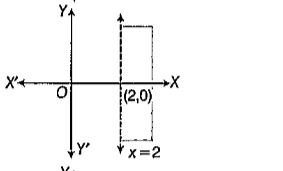 D
D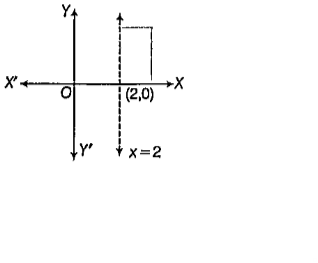
The solution set of the inequation 15+3x≤0 is
Ax∈(−53,∞)Bx∈(−∞,53)Cx∈(53,∞)Dx∈(∞,−53)
Graph the solution sets of the following inequations:
x−y≤3
View SolutionGraph the solution sets of the following inequations:
y−2≤3x
View SolutionFind the solutions set of inequalities 0≤x≤5,0≤2y≤7
View SolutionThe solution set of the inequalities 2x+y≥4,x+y≤x,2x−3y≤6 is
View SolutionThe graphical solution of linear inequalities x+y≥5 and x−y≤3,
View Solution