A company produces two types of goods A and B, that require gold and silver. Each unit of type A requires 3 g of silver and 1 g of gold while that of type B requires 1 g of silver and 2 g of gold. The company can procure a maximum of 9 g of silver and 8 g of gold. If each unit of type A brings a profit of < 40 and that of type B < 50, formulate LPP to maximize profit.
The correct Answer is:Max Z = 25000 at x =100/3 , y = 70/3
Step by step video, text & image solution for A company produces two types of goods A and B, that require gold and silver. Each unit of type A requires 3 g of silver and 1 g of gold while that of type B requires 1 g of silver and 2 g of gold. The company can procure a maximum of 9 g of silver and 8 g of gold. If each unit of type A brings a profit of < 40 and that of type B < 50, formulate LPP to maximize profit. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUESTION BANK 2021Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:QUESTION BANK 2021Exercise:Part II LINEAR PROGRAMMING PROBLEMS (E. Activities)
Explore 3 Videos
- QUESTION BANK 2021Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:QUESTION BANK 2021Exercise:Part II ASSIGNMENT PROBLEMS AND SEQUENCING (I. Select and write the most appropriate answer from the given alternatives for each sub question.)
Explore 12 Videos
- QUESTION BANK 2021Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:QUESTION BANK 2021Exercise:Part II LINEAR PROGRAMMING PROBLEMS (C. Fill in each of the following blanks)
Explore 12 Videos
- PROBABILITY DISTRIBUTIONBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:PROBABILITY DISTRIBUTIONExercise:MULTIPLE CHOICE QUESTIONS
Explore 9 Videos
- THREE DIMENSIONAL GEOMETRY Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:THREE DIMENSIONAL GEOMETRY Exercise:MULTIPLE CHOICE QUESTIONS
Explore 8 Videos
Similar Questions
A company produces two types of belts A and B. Profits on these belts are Rs. 2 and Rs. 1.50 per belt respectively. A belt of type A requires twice as much time as belt of type B. The company can produce at most 1000 belts of type B per day. Material for 800 belts per day is available. At most 400 buckles for belts of type A and 700 for type B are available per day. How much belts of each type should the company produce so as to maximise the profit?
View SolutionA company produces two types of leather belts A and B on which the profits are Rs. 40 and Rs. 30 per belt respectively. Each belt of type A requires twice as much time as required by a belt to type B.If all belts were of type B the company could produce 1000 belts per day. But the supply of leather is sufficient only for 800 belts per day. Belt A requires a fancy buckle and only 400 fancy buckles are available per day. For belt of type B only 700 buckles are available per day. How should the company manufacture the two types of belts in order to have maximum overall profit?
View Solution
Knowledge Check
A company manufactures two types of telephone sets A and B . The A type telephone requires 2 hour and B type telephone requires 2 hour and B type telephone requires 4 hours to make . The company has 800 work hours per day . 300 telephones can pack in a day . The selling prices of A and B type telephones are Rs.300 and 400 respectively . For maximum profits company produces x telephones of a type and y telephones of B types . Then except x≥0andy≥0 , linear constraints and the probable region of the LPP is of the type .
Ax+2y≤400,x+y≤300,
Max z = 300x +400y, boundedB2x+y≤400,x+y≥300,
Max z = 400x +300y, unboundedC2x+y≥400,x+y≥300,
Max z = 300x +400y, parallelogramD2x+y≤400,x+y≥300,
Max z = 300x +400y, square
A manufacturing company makes two types of teaching aids A and B . Each type of A requires 9 labour hours for fabricating and 1 labour hours for finishing.Each type of B requires 12 labour hours for fabricating and 3 labour hours for finishing.For fabricating and finishing, the maximum labour hours abailable per week are 180 and 30 respectively.The company makes a profit of ₹ 80 on each type A and ₹ 120 on each type B. How many pieces of type A and type B should be manufactured per week to get a maximum profit? Make it as an LPP and solve graphically.What is the maximum profit per week?
View SolutionA manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the time (in minutes) required for each purpose and the time (in minutes) required for each toy on the machines is given below:
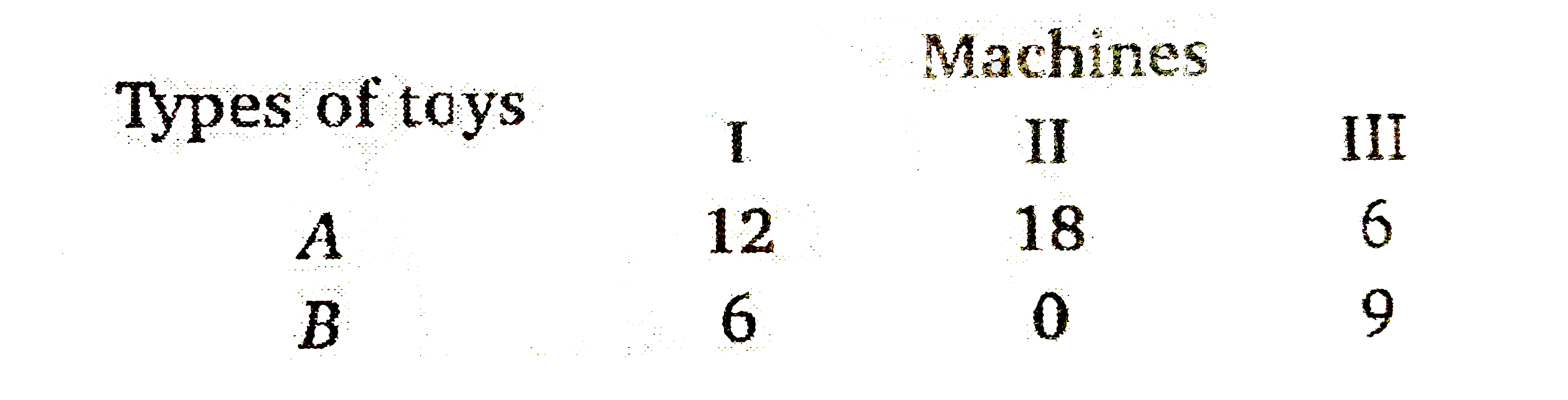
Each machine is available for a maximum of 6 hours per day. If the profit on each toy of type A is Rs. 7.50 and that on each toy of type B is Rs. 5, show that 15 toys of type A and 30 of type B should be manufactured in a day to get maximum profit.
View SolutionA company manufactures two types of toys A and B. Type A requires 5 minutes each for cutting and 10 minutes each for assembling. Type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours available for cutting and 4 hours available for assembling in a day. He earns a profit of Rs.50 each on type A and Rs.60 each on type. B. How many toys of each type should the company manufacture in a day to maximize the profit ?
View SolutionSilver has an atomic radius of 144 pm and the density of silver is 10.6 g cm–3 . To which type of cubic crystal, silver belongs?
View SolutionCalculate the number of coulombs required to deposit 50 g of silver at cathode from silver nitrate solution.
(Atomic mass of silver = 108)
View SolutionA manufacturing company makes two types of teaching aids A and B . Each type of A requires 9 labour hours for fabricating and 1 labour hours for finishing.Each type of B requires 12 labour hours for fabricating and 3 labour hours for finishing.For fabricating and finishing, the maximum labour hours abailable per week are 180 and 30 respectively.The company makes a profit of ₹ 80 on each type A and ₹ 120 on each type B. How many pieces of type A and type B should be manufactured per week to get a maximum profit? Make it as an LPP and solve graphically.What is the maximum profit per week?
View SolutionA copany manufactures two types of toys, A and B. Type A requires 5 minutes each for cutting and 10 minutes each for assembling. Type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours available for cutting and 4 hours available for assembling in a day. The profit is Rs.50 each on type A and Rs.60 each on type B. How many toys of each type should the company manufacture in a day to maximize the profit?
View Solution

