If the regression equation x on y is 3x+2y=26 then bxy equals to
3/2
2/3
−3/2
−2/3
The correct Answer is:D
To find the regression coefficient bxy from the regression equation 3x+2y=26, we can follow these steps:
Step 1: Rearrange the regression equation
Start with the given regression equation:
3x+2y=26
We want to express x in terms of y. To do this, isolate x:
3x=26−2y
Now, divide both sides by 3:
x=26−2y3
Step 2: Simplify the equation
Rewrite the equation:
x=−23y+263
This is now in the form x=bxyy+a, where bxy is the slope of the line.
Step 3: Identify the regression coefficient
From the equation x=−23y+263, we can see that:
bxy=−23
Conclusion
Thus, the value of bxy is:
bxy=−23
Start with the given regression equation:
3x+2y=26
We want to express x in terms of y. To do this, isolate x:
3x=26−2y
Now, divide both sides by 3:
x=26−2y3
Rewrite the equation:
x=−23y+263
This is now in the form x=bxyy+a, where bxy is the slope of the line.
From the equation x=−23y+263, we can see that:
bxy=−23
Thus, the value of bxy is:
bxy=−23
Topper's Solved these Questions
- QUESTION BANK 2021Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:QUESTION BANK 2021Exercise:Part II 3. LINEAR REGRESSION (II State whether the following statements are true or false:)
Explore 17 Videos
- QUESTION BANK 2021Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:QUESTION BANK 2021Exercise:Part II 3. LINEAR REGRESSION (III. Fill in the following blanks:)
Explore 11 Videos
- QUESTION BANK 2021Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:QUESTION BANK 2021Exercise:Part II 2. Insurance and Annuity (Activity based Question)
Explore 3 Videos
- PROBABILITY DISTRIBUTIONBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:PROBABILITY DISTRIBUTIONExercise:MULTIPLE CHOICE QUESTIONS
Explore 9 Videos
- THREE DIMENSIONAL GEOMETRY Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:THREE DIMENSIONAL GEOMETRY Exercise:MULTIPLE CHOICE QUESTIONS
Explore 8 Videos
Similar Questions
The regression equation of x on y is 40x-18y = 214… (i)
The regression equation of y on x is 8x -10y +66 =0….. (ii)
Solving equations i and ii,
¯x=□
¯y=□
∴byx=□□
∴bxy=□□
∴r=□
View Solution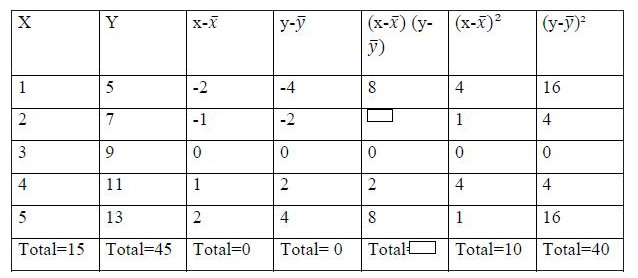
Mean of x=¯x=□
Mean y=¯y=□
bxy=□□
byx=□□
Regression equation of x on y is x−¯x=bxy(y−¯y)
∴ Regression equation of x on y is □
Regression equation of y on x is y−¯y=byx(x−¯x)
∴ Regression equation of y on x is □
View Solution
Knowledge Check
In the regression equation of X on Y
AX is independent and Y is dependent.BY is independent and X is dependent.CBoth X and Y are independent.DBoth X and Y are dependent.If the regression equation of y is y=λx+4 and that of X on Y be 4x=y-5 then
A0<4λ≤1B0≤λ≤4C0<λ≤4DNone of theseRegression equation of yon is 8x-10y+66=0 σx=3. Hence cov(x,y) is equal to
A11,25B7.2C2,4DNone of these
If 2x+3y−1=0 is the regression line of y on x, then byx is ……………..
View Solution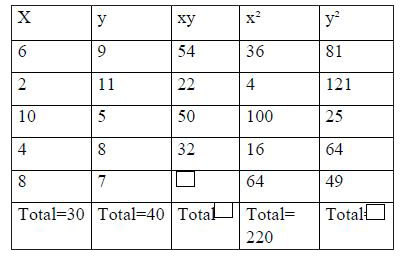
bxy=□□
byx=□□
∴ Regression equation of x on y is □
∴ Regression equation of y on x is □
View SolutionThe regression equation of y on x is 2x-5y +60 =0.
Mean of x = 18
∴¯y=□
σx:σy=3:2
∴byx=□□
∴r=□
View SolutionState True or False: The equations of two regression lines are 10x−4y=80 and 10y−9x=40 . then bxy=0.9
View SolutionRegression equation of Y on X 2x+3y-12=0. The value of byx is
View Solution

