Regression equation of Y on X 2x+3y-12=0. The value of byx is
The correct Answer is:A
To find the value of the regression coefficient byx from the regression equation of Y on X, given by the equation 2x+3y−12=0, we can follow these steps:
Step 1: Rearranging the Equation
We start with the regression equation:
2x+3y−12=0
We can rearrange this equation to express y in terms of x:
3y=12−2x
Step 2: Solve for y
Now, we divide the entire equation by 3 to isolate y:
y=123−23x
y=4−23x
Step 3: Identify the Coefficient of x
In the equation y=4−23x, we can identify the coefficient of x. The coefficient of x is:
−23
Step 4: Determine byx
The coefficient of x in the regression equation of Y on X is equal to byx:
byx=−23
Final Answer
Thus, the value of byx is:
−23
---
We start with the regression equation:
2x+3y−12=0
3y=12−2x
Now, we divide the entire equation by 3 to isolate y:
y=123−23x
y=4−23x
In the equation y=4−23x, we can identify the coefficient of x. The coefficient of x is:
−23
The coefficient of x in the regression equation of Y on X is equal to byx:
byx=−23
Thus, the value of byx is:
−23
Topper's Solved these Questions
- STATISTICSBook:FIITJEEChapter:STATISTICSExercise:Assignment Problems (Objective) Level II
Explore 25 Videos
- STATISTICSBook:FIITJEEChapter:STATISTICSExercise:Assertion -Reasoning Type MCQ Single Correct(Level II)
Explore 2 Videos
- STATISTICSBook:FIITJEEChapter:STATISTICSExercise:Assignment Problems (Subjective)
Explore 14 Videos
- SET, RELATION & FUNCTIONBook:FIITJEEChapter:SET, RELATION & FUNCTIONExercise:Exercise 3
Explore 8 Videos
- STRAIGHT LINE Book:FIITJEEChapter:STRAIGHT LINE Exercise:NUMERICAL BASED
Explore 4 Videos
Similar Questions
Knowledge Check
In the regression equation of X on Y
AX is independent and Y is dependent.BY is independent and X is dependent.CBoth X and Y are independent.DBoth X and Y are dependent.Regression equation of yon is 8x-10y+66=0 σx=3. Hence cov(x,y) is equal to
A11,25B7.2C2,4DNone of theseIf the regression equation x on y is 3x+2y=26 then bxy equals to
A3/2B2/3C−3/2D−2/3
If x=3k−2,y=2k is a solution of equation 4x−7y+12=0 then value of k is
View SolutionThe equations of the two lines of regression are 3x+y=5 and 2x+3y=6. Find
(a) The regression line of Y and X.
(b) mean values of x and y
(c) correlation coefficient x and y
(d) the angle between the regression lines.
View Solution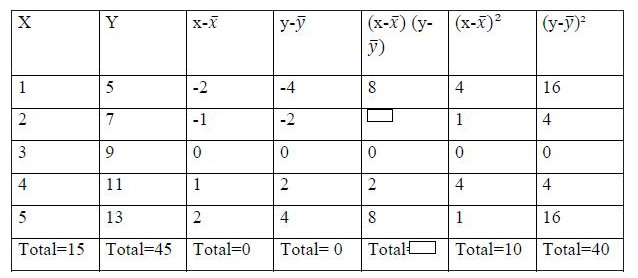
Mean of x=¯x=□
Mean y=¯y=□
bxy=□□
byx=□□
Regression equation of x on y is x−¯x=bxy(y−¯y)
∴ Regression equation of x on y is □
Regression equation of y on x is y−¯y=byx(x−¯x)
∴ Regression equation of y on x is □
View SolutionState True or False: If equation of regression lines are 3x+2y−26=0 and 6x+y−31=0 then mean of x is 7.
View SolutionAre the following statement correct? Given the reasons:
(a) The regression coefficient of X and Y is 3.2 and that of y on x is 0.8.
(b) The regression coefficient of X and Y is -2.5 and the correlation coefficient is 0.3.
View Solution

