In the following circuit the switch is closed at t=0.Intially there is no current in inductor.Find out current the inductor coil as a function of time.
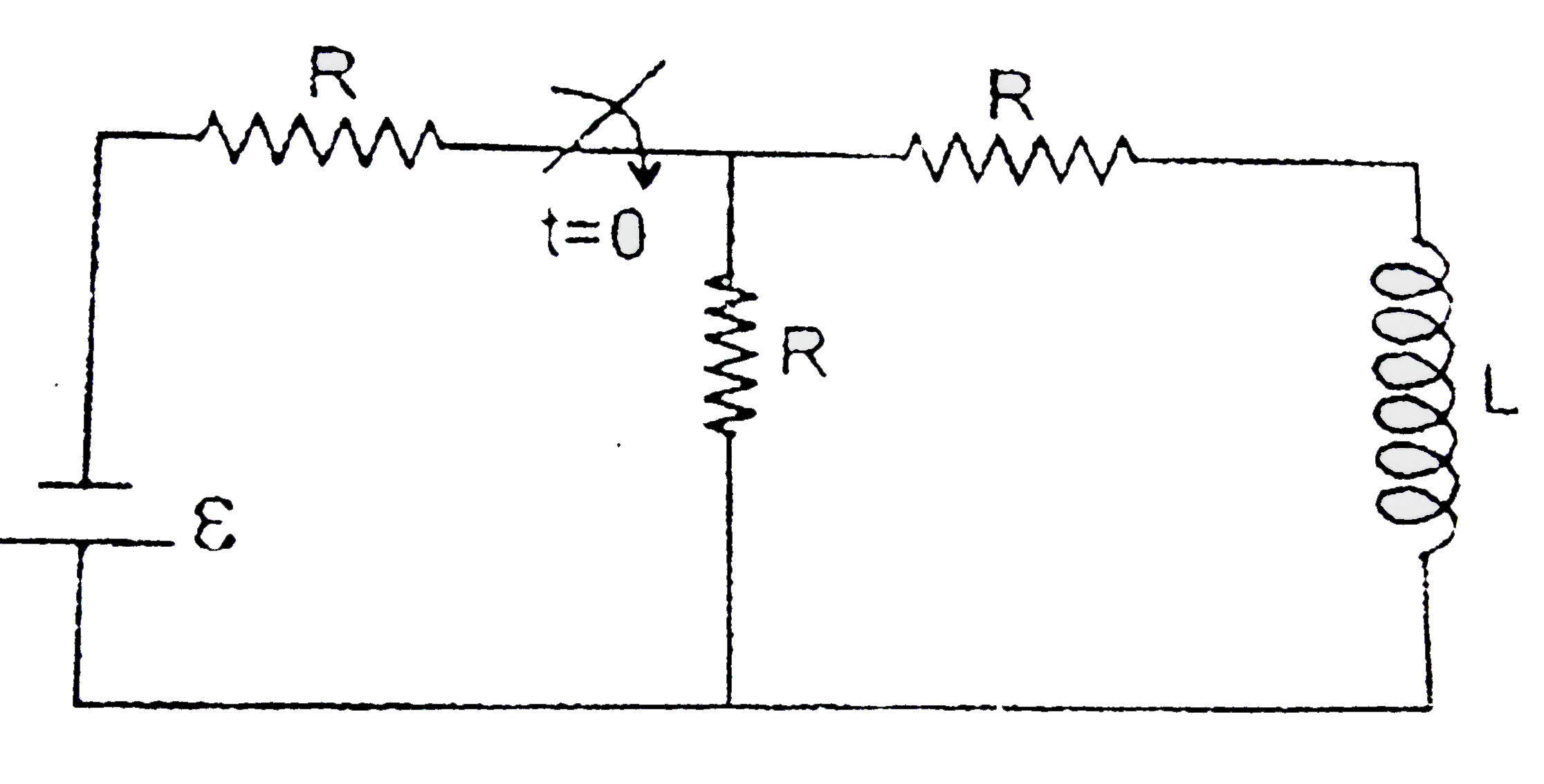
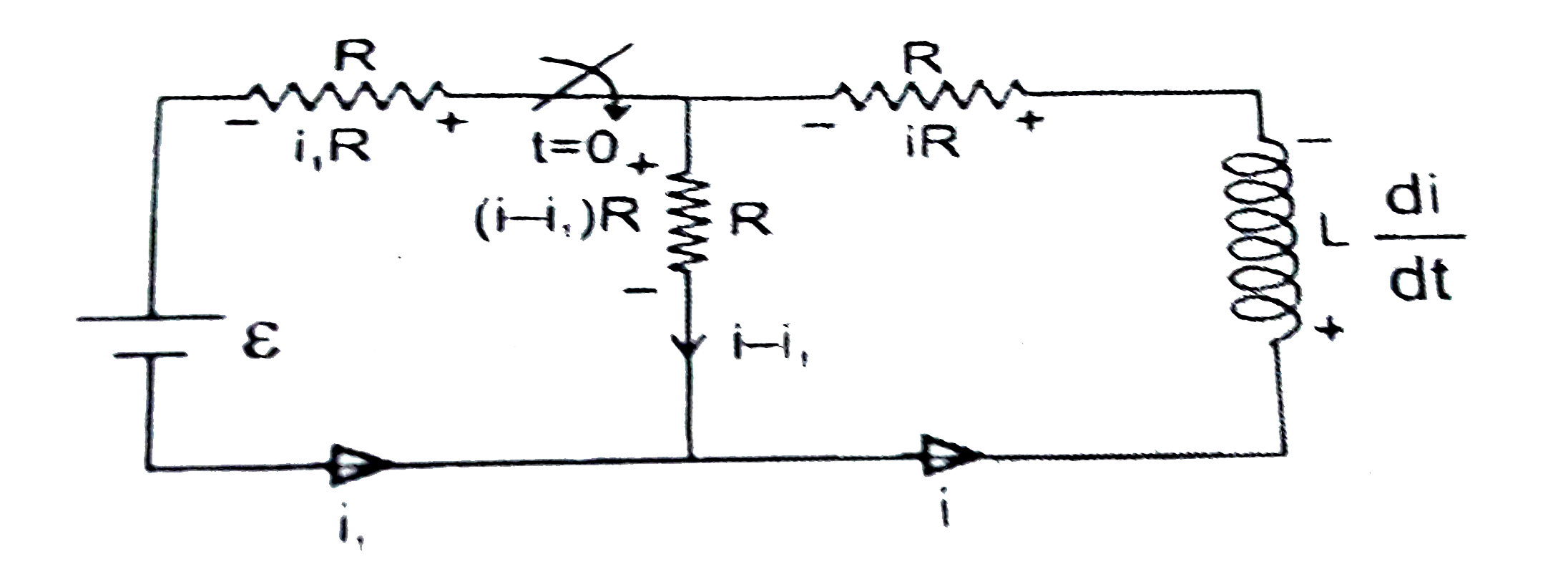
At any time t
−ε+i1R−(i−i1)R=0
−ε+2i1R−iR=0
i1=iR+ε2R Now,−ε+i1R+iR+L.didt=0
=ε+(iR+ε2)+iR+L.didt=0 ⇒=ε2+3iR2=−L.didt
(−ε+3iR2)dt=−L.di ⇒−−dt2L=di−ε+3iR
−∫t0dt2L=∫i0di−ε+3iR ⇒−t2L=13RIn(−ε+3iR−ε)
−In(−ε+3iR−ε)=3Rt2L ⇒i=+ε3R(1−e−3Rt2L)
Similar Questions
In the following circuit (Fig.)the switch is closed at t=0. Intially, there is no current in inductor. Find out the equation of current in the inductor coil as s function of time.
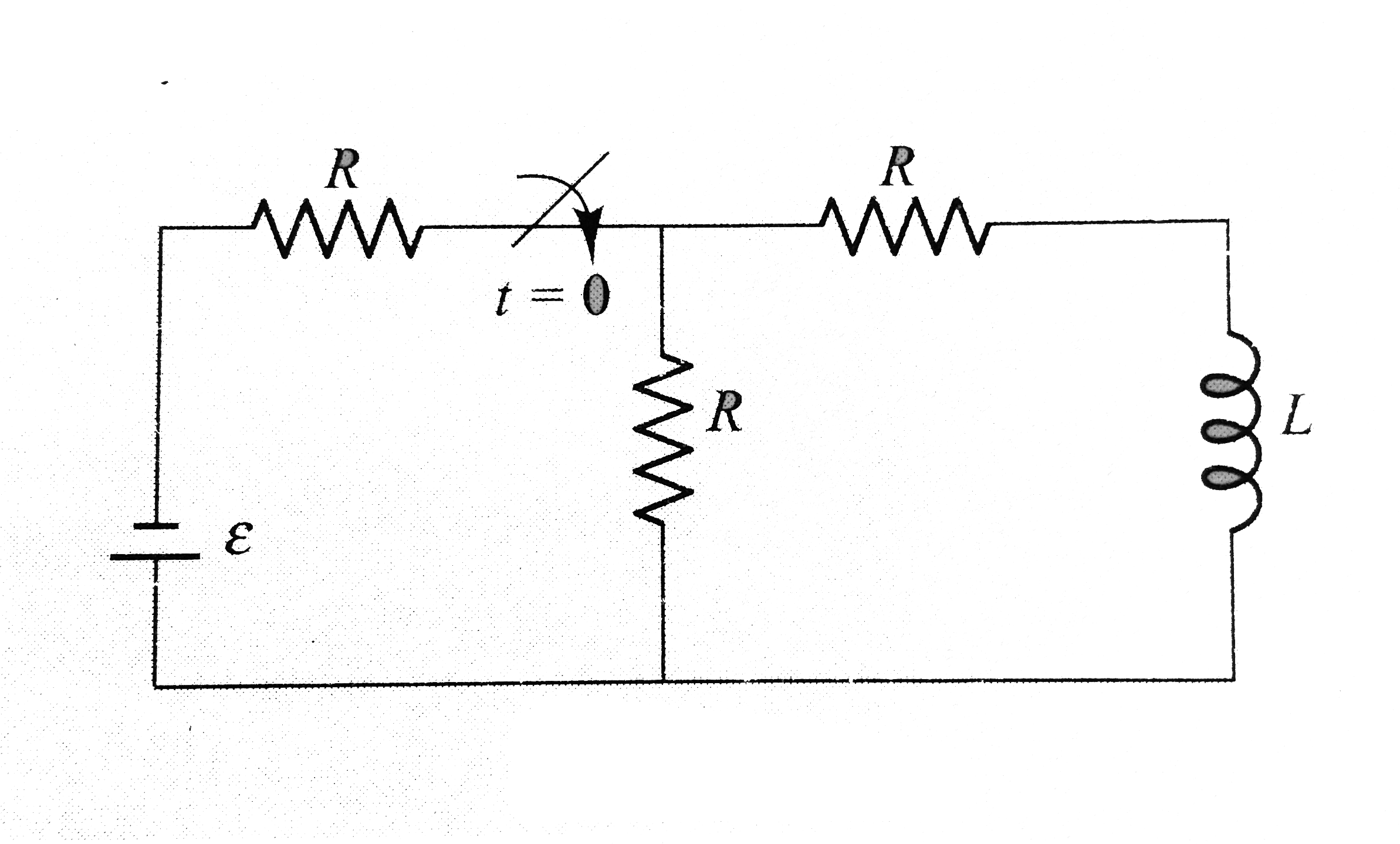
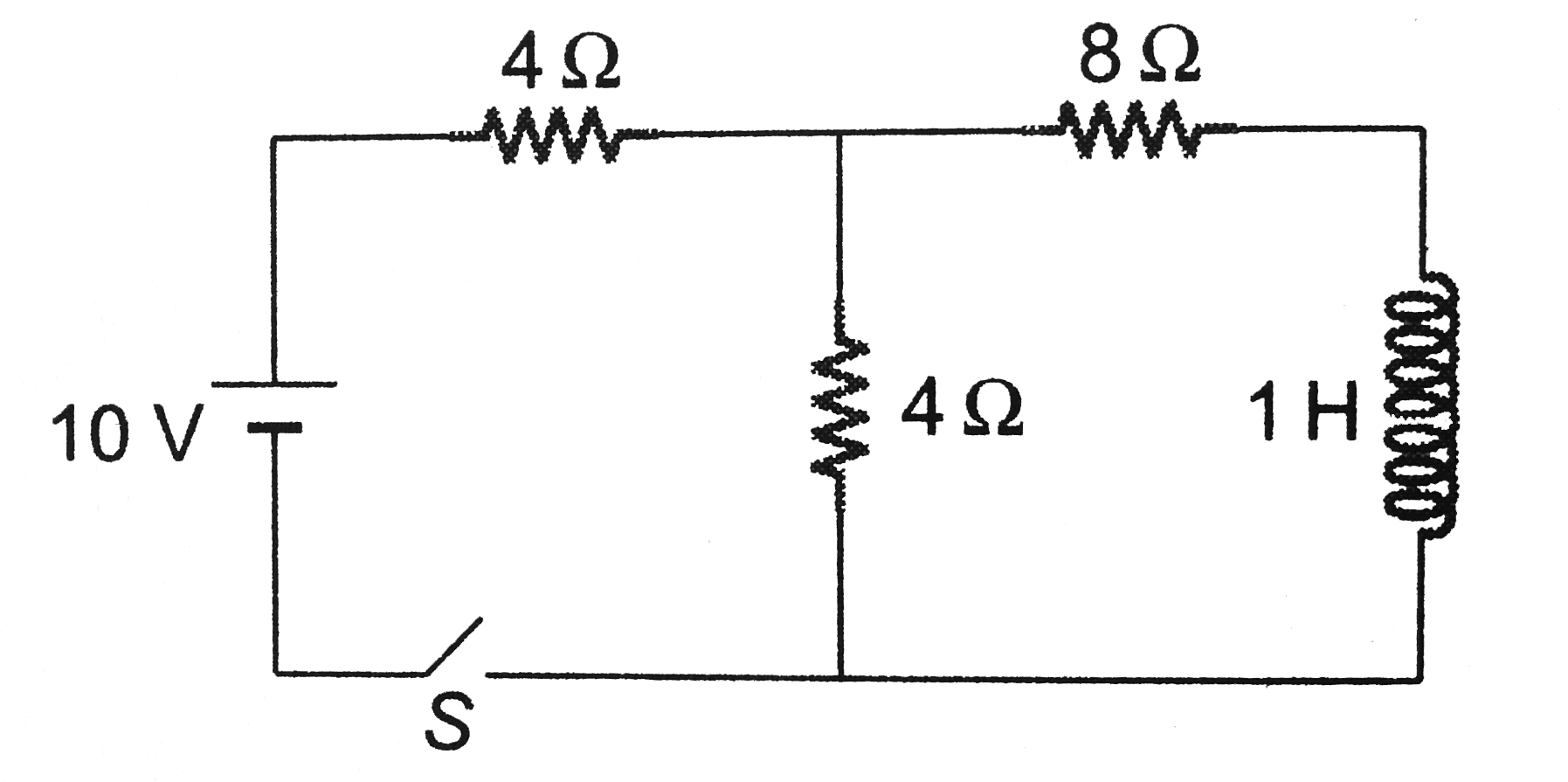
View SolutionThe switch in figure is closed at time t=0. Find the current in the inductor and the current through the switch as functions of time thereafter.
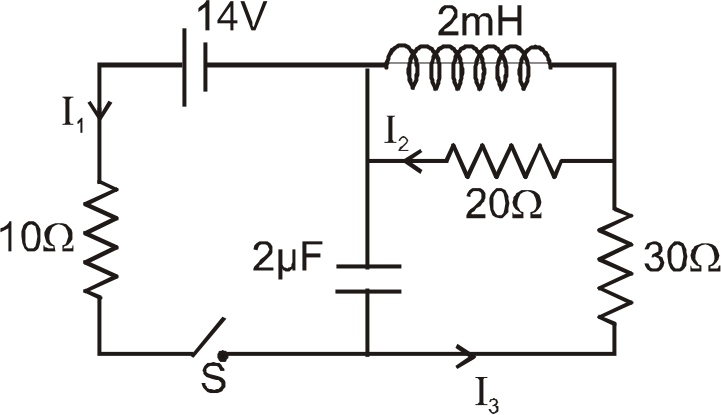
View SolutionIn the circuit shown, the switch is closed at t=0, the currents I1,I2 and I3 are
View SolutionIn the circuit shown, switch S is closed at time t=0. Find the current through the inductor as a function of time t.

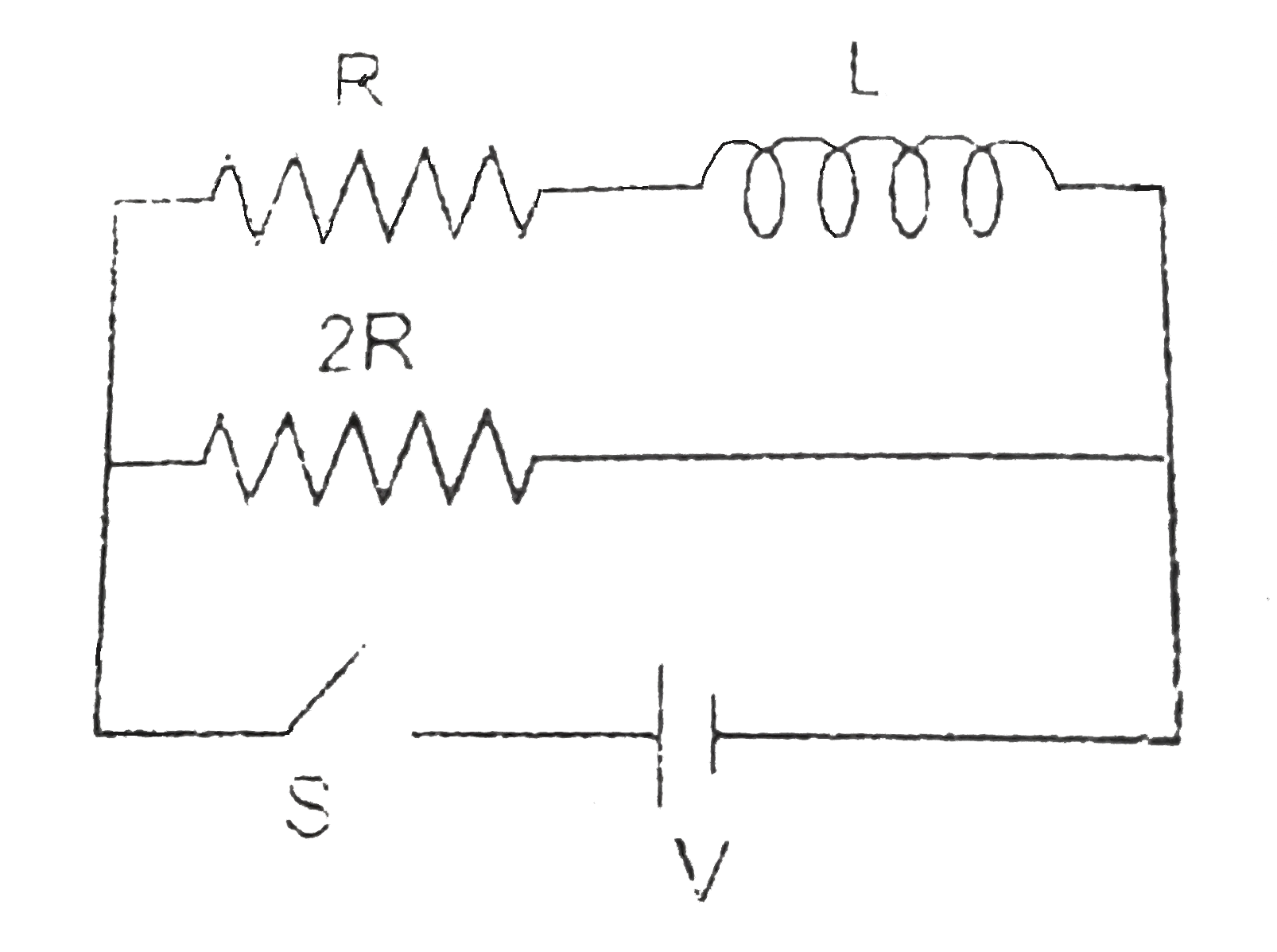
View SolutionConsider a L-R circuit shown in figure. There is no current in circuit switch S is closed at t = 0, time instant when current in inductor is equal to current in resistor 2R will be :
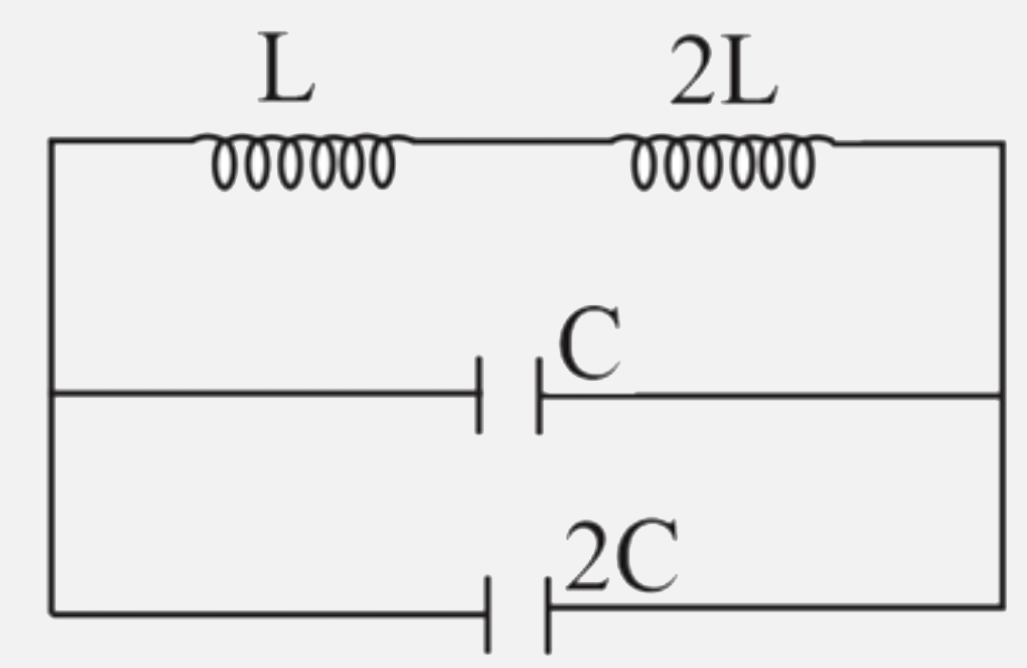
View SolutionThe frequency of oscillation of current in the inductor is -
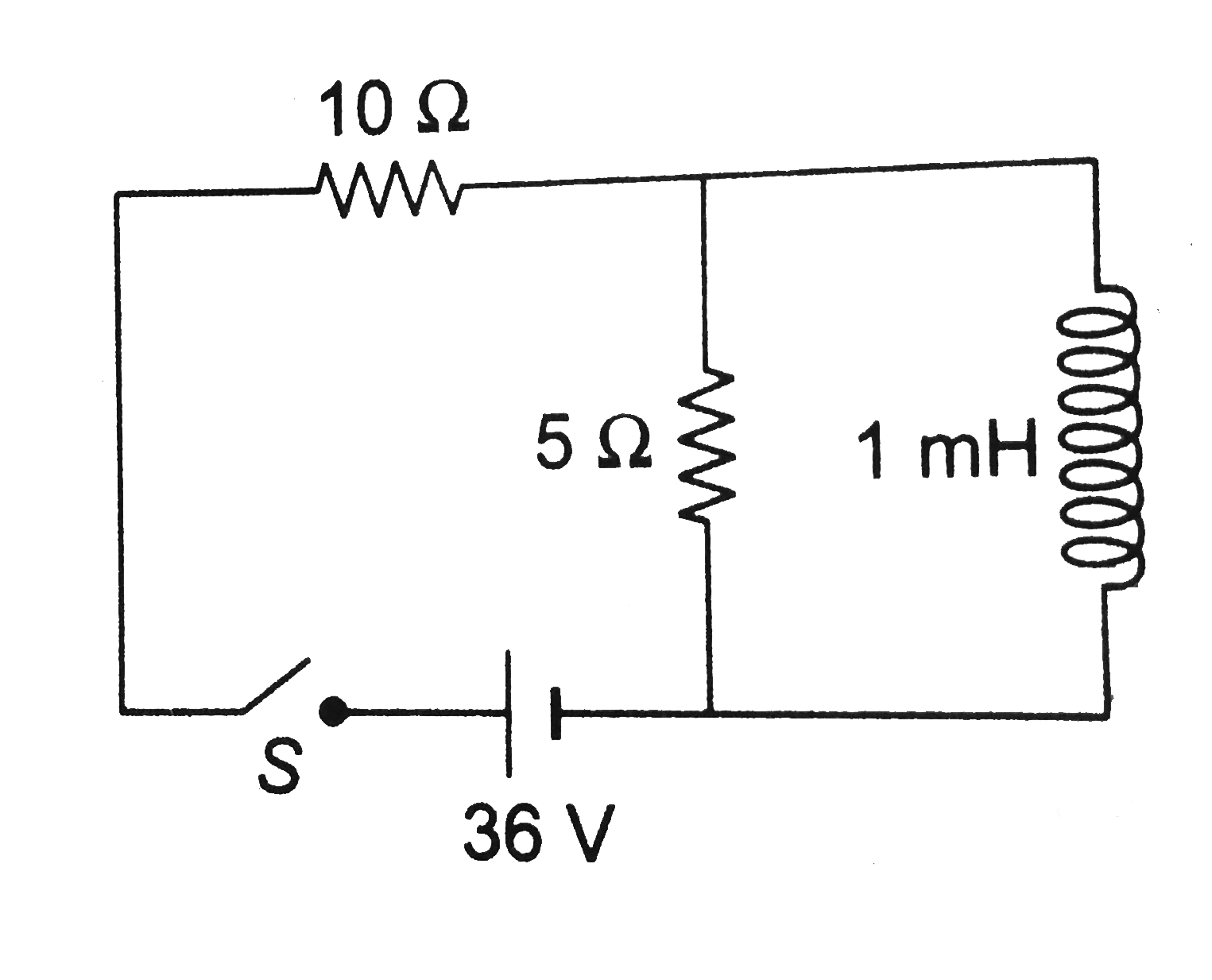
View SolutionIn the circuit arrangement shown in figure, the switch S is closed at t=0. Find the current in the inductance as a function of time? Does the current through 10Ω resistor vary with time or remains constant.
View SolutionThe frequency of oscillation of current in the inductor is:
View SolutionSwitch is closed at t=0 then the current in the circuit at t=L2R is
_PHY_E06_157_Q01.png)
View SolutionIn the following circuit (Fig.) the switch is closed at t=0. Find the current i1,i2,i3 and di3/dt at t=0 and at t=∞. Initially, all current are zero.

View Solution
