One mole of a monoatomic real gas satisfies the equation p(V−b)=RT where b is a constant. The relationship of interatomic potential V(r) and interatomic distance r for the gas is given by:




The correct Answer is:C
P(V−b)=RT
⇒PV=Pb=RT
⇒PVRT=PbRT+1
⇒Z=1+PbRT
Hence Z>1 at all pressure.
This means, repulsive tendencies will be dominant when interatomic distance are small.
This means, interatomic potential is never negative but becomes positive at small interatomic distances.
Hence answer is (C )
Topper's Solved these Questions
- GASEOUS STATEBook:RESONANCE ENGLISHChapter:GASEOUS STATEExercise:Exercise-3
Explore 1 Video
- GASEOUS STATEBook:RESONANCE ENGLISHChapter:GASEOUS STATEExercise:Exercise-2
Explore 1 Video
- FUNDAMENTAL CONCEPTBook:RESONANCE ENGLISHChapter:FUNDAMENTAL CONCEPTExercise:ORGANIC CHEMISTRY(Fundamental Concept )
Explore 40 Videos
- HYDROCARBONBook:RESONANCE ENGLISHChapter:HYDROCARBONExercise:ORGANIC CHEMISTRY(Hydrocarbon)
Explore 50 Videos
Similar Questions
One mole of a monoatomic real gas satisfies the equation p(V−b)=RT where b is a constant. The relationship of interatomic potential V(r) and interatomic distance r for gas is given by
View SolutionA gas obeys the equation of state P(V−b)=RT (The parameter b is a constnat The slope for an isochore will be .
View SolutionIn a process, temperature and volume of one mole of an ideal monoatomic gas are varied according to the relation VT= K, where K is a constant. In this process the temperataure of the gas is increased by ΔT. The amount of heat absorbed by gas is (R is gas constant).
View SolutionIn a process, temperature and volume of one mole of an ideal monoatomic gas are varied according to the relation VT= K, where K is a constant. In this process the temperataure of the gas is increased by ΔT. The amount of heat absorbed by gas is (R is gas constant).
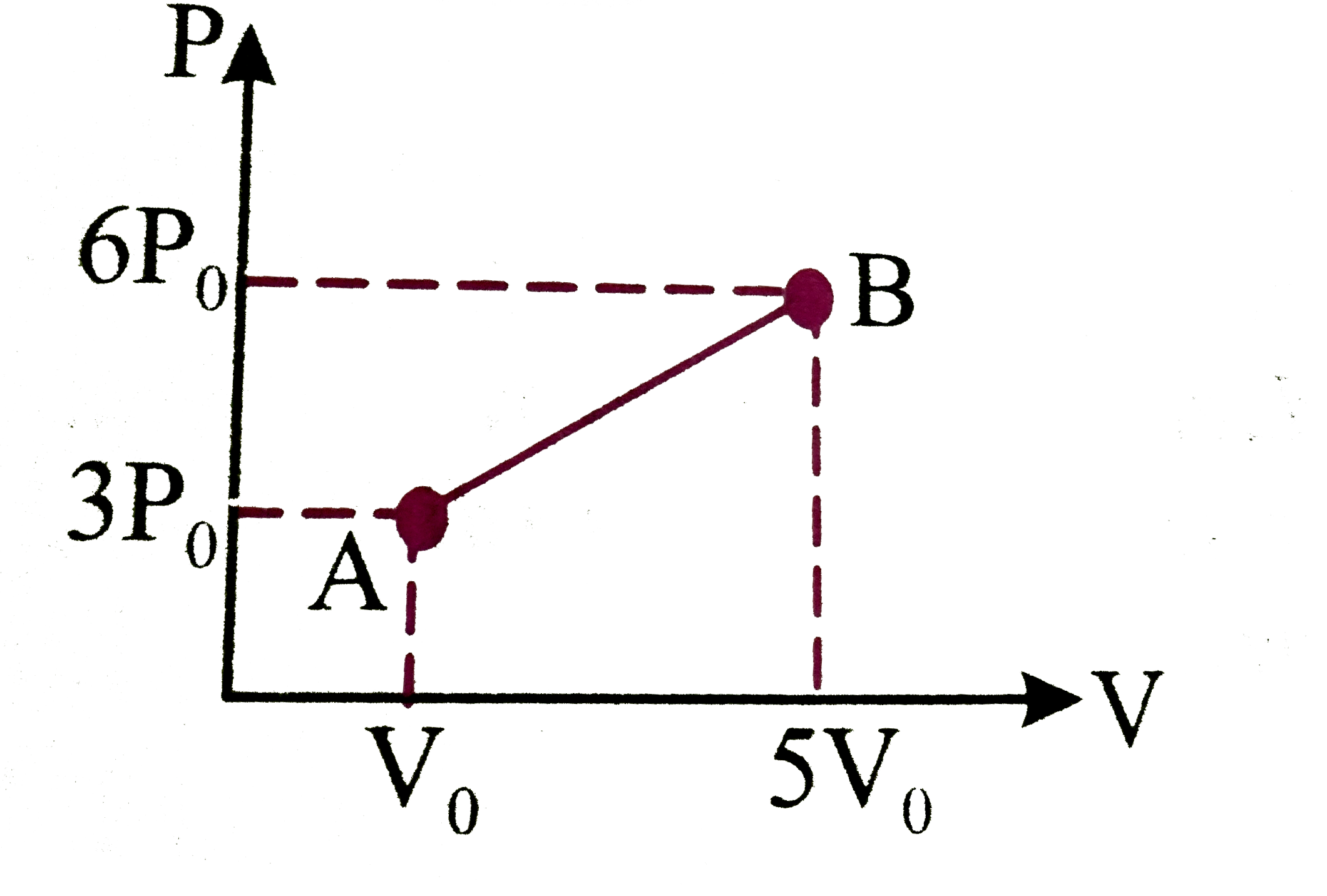
View SolutionOne mole of a monoatomic ideal gas undergoes the process A→B in the given P-V diagram. What is the specific heat for this process?
View SolutionOne mole of a diatomic gas undergoes a process P=P0/[1+(V/V30)] where P0 and V0 are constant. The translational kinetic energy of the gas when V=V0 is given by
View SolutionOne mole of an ideal monoatomic gas is taken through a polytropic process P2T = constant. The heat required to increase the temperature of the gas by ΔT is
View SolutionOne mole of an ideal monatomic gas undergoes the process P=αT1/2, where α is constant . If molar heat capacity of the gas is βR1 when R = gas constant then find the value of β.
View Solution1 mol of a real gas obeys P(Vm−b)=RT , where 'b' and 'R' are constants. If the compressibility factor of gas is 1.11 and occupied volume of the gas is Xb then determine value of X/2.
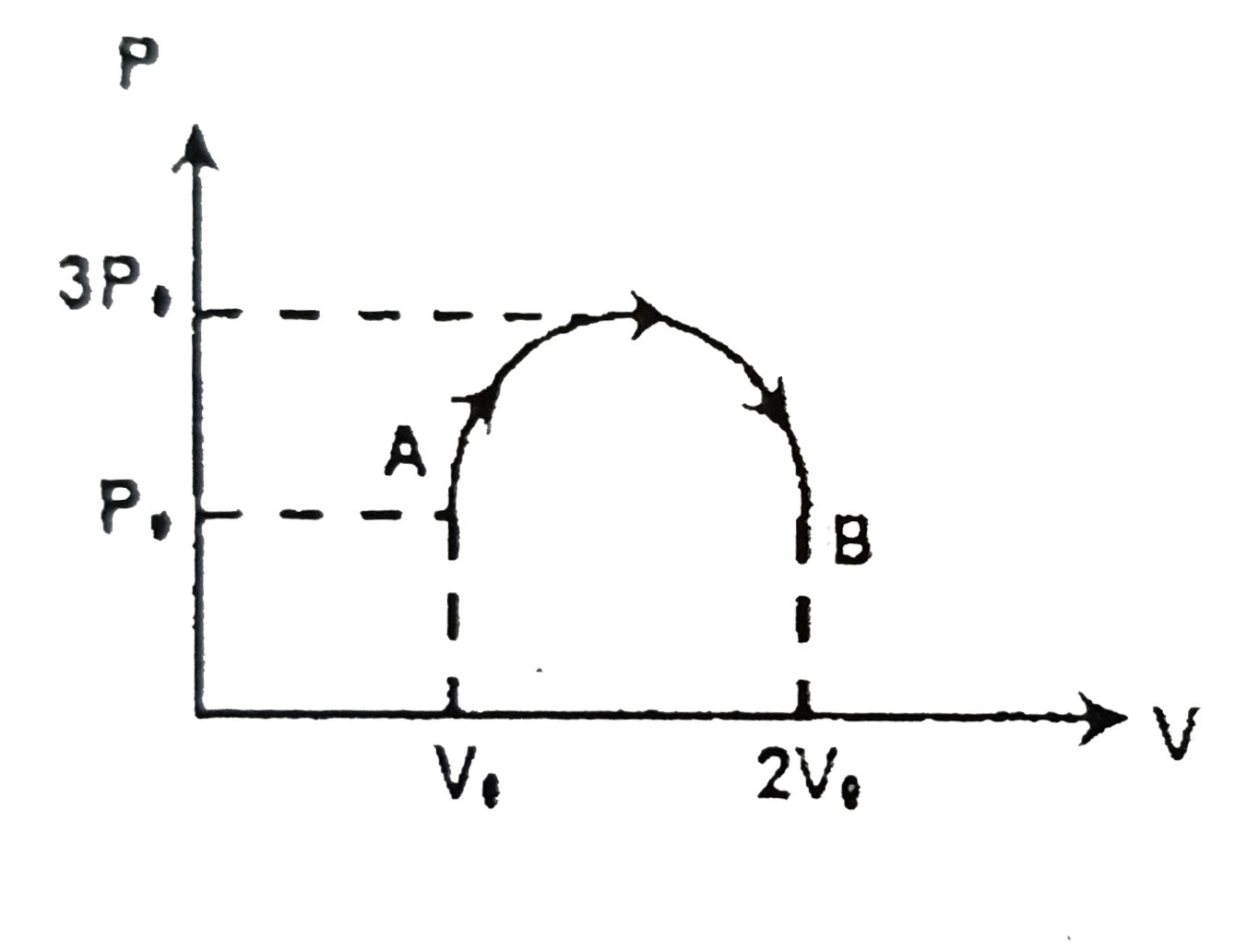
View SolutionOne mole of an ideal monoatomic gas is taken through the thermodynamic process shown in the P−V diagram. The heat supplied to the system is
View Solution

