A scientist proposed the following equation of state P=RTVm−BV2m+CV3m. If this equation leads to the critical behavior then critical temperature is:
8B27RC
B8RC
B23RC
None of these
The correct Answer is:C
To find the critical temperature from the given equation of state P=RTVm−BV2m+CV3m, we can follow these steps:
Step 1: Understand the given equation of state
The equation provided is a modified form of the ideal gas law, where P is the pressure, R is the universal gas constant, T is the temperature, and Vm is the molar volume. The terms involving B and C account for deviations from ideal gas behavior.
Step 2: Identify the critical constants
In the context of real gases, the critical temperature can be derived from the general form of the van der Waals equation or similar equations of state. The critical temperature Tc is related to the coefficients in the equation.
Step 3: Compare with known equations
From the van der Waals equation, we know that the critical temperature can be expressed as:
Tc=8a27Rb
where a and b are constants related to the specific gas.
Step 4: Relate the constants in the given equation to a and b
In the given equation:
- The term B corresponds to a (the attraction parameter).
- The term C can be related to b (the volume excluded due to finite size of molecules).
Step 5: Establish relationships
From the comparison:
- We can assume B is negligible in the context of critical behavior.
- The relationship between C and B can be established as C=aB.
Step 6: Substitute into the critical temperature formula
Substituting B and C into the critical temperature formula:
Tc=8B27RandB=Cb
Thus,
Tc=8(Cb)27R
Step 7: Final expression for critical temperature
Rearranging gives:
Tc=8C27Rb
This shows how the critical temperature is derived from the coefficients in the equation of state.
Final Answer
The critical temperature Tc can be expressed as:
Tc=8B227RC
The equation provided is a modified form of the ideal gas law, where P is the pressure, R is the universal gas constant, T is the temperature, and Vm is the molar volume. The terms involving B and C account for deviations from ideal gas behavior.
In the context of real gases, the critical temperature can be derived from the general form of the van der Waals equation or similar equations of state. The critical temperature Tc is related to the coefficients in the equation.
From the van der Waals equation, we know that the critical temperature can be expressed as:
Tc=8a27Rb
where a and b are constants related to the specific gas.
In the given equation:
- The term B corresponds to a (the attraction parameter).
- The term C can be related to b (the volume excluded due to finite size of molecules).
From the comparison:
- We can assume B is negligible in the context of critical behavior.
- The relationship between C and B can be established as C=aB.
Substituting B and C into the critical temperature formula:
Tc=8B27RandB=Cb
Thus,
Tc=8(Cb)27R
Rearranging gives:
Tc=8C27Rb
This shows how the critical temperature is derived from the coefficients in the equation of state.
The critical temperature Tc can be expressed as:
Tc=8B227RC
Topper's Solved these Questions
- GASEOUS STATEBook:RESONANCE ENGLISHChapter:GASEOUS STATEExercise:Exercise-3
Explore 1 Video
- GASEOUS STATEBook:RESONANCE ENGLISHChapter:GASEOUS STATEExercise:Exercise-2
Explore 1 Video
- FUNDAMENTAL CONCEPTBook:RESONANCE ENGLISHChapter:FUNDAMENTAL CONCEPTExercise:ORGANIC CHEMISTRY(Fundamental Concept )
Explore 40 Videos
- HYDROCARBONBook:RESONANCE ENGLISHChapter:HYDROCARBONExercise:ORGANIC CHEMISTRY(Hydrocarbon)
Explore 50 Videos
Similar Questions
Critical constants are related with van der waals' constant as follows:
Vc=3b,Pc=a27b2,Tc=8a27Rb
The pressure required to liquefy a gas at the critical temperature is called :
View SolutionThe equation of PcVcRTc = ..........
View SolutionIn a gas equation, PV=RT,V refers to the volume of
View SolutionThe equation of state for real gas is given by ((p+aV2(V−b)=RT. The dimension of the constant a is ………………. .
View SolutionIf va,vhandvm and are the speeds of sound in air, hydrogen and a metal at the same temperature, then
View SolutionUse of dilution formula (M1V1=M2V2)

View Solution(p - V) diagram of (n) moles of an ideal gas is as shown in figure. Find the maximum temperature between (A) and (B).
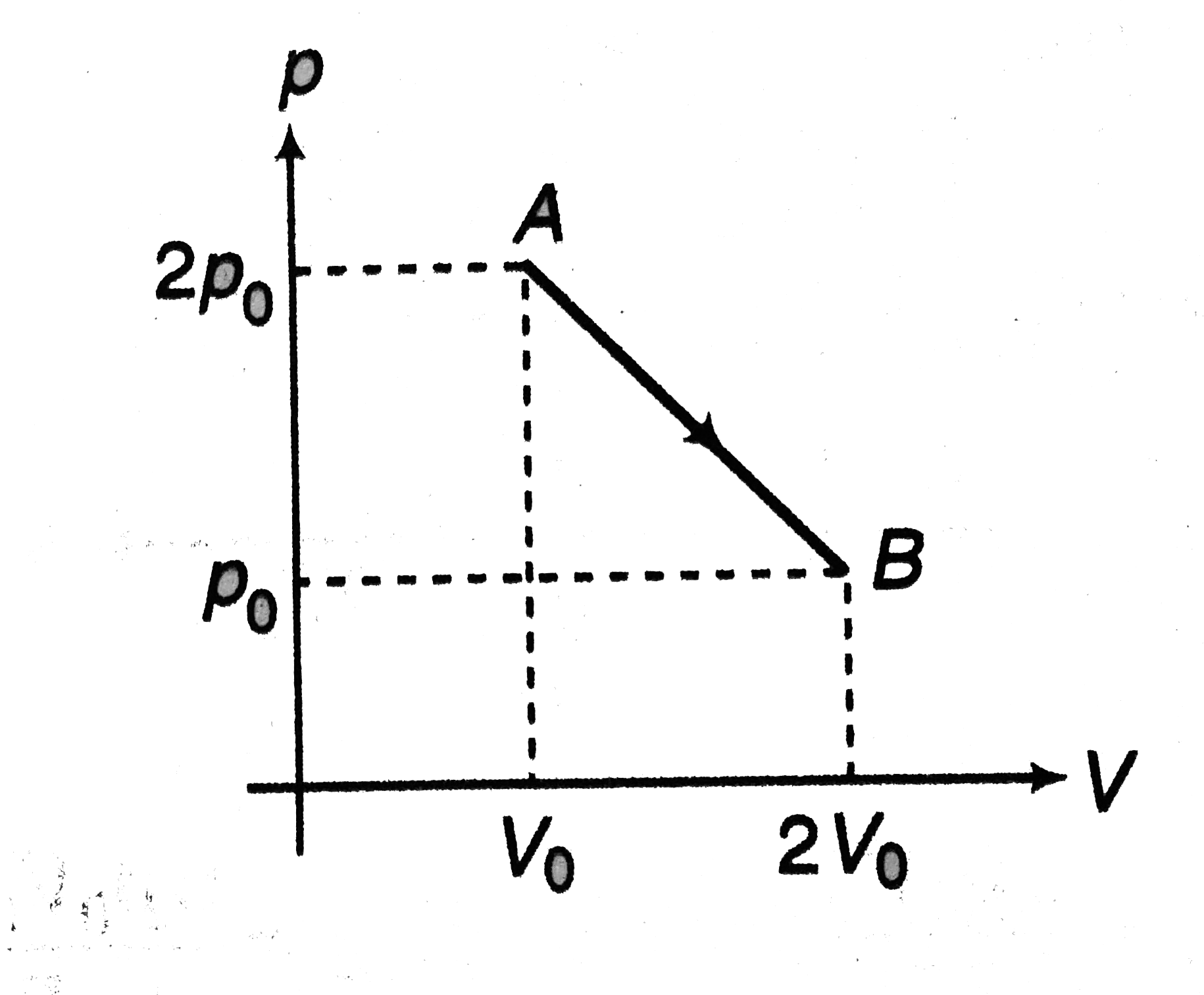 .
.
How to proceed For given number of moles of a gas,
T∝pV(pV=nRT)
Although (pV)A=(pV)B=2p0V0orTA=TB, yet it is not an isothermal process. Because in isothermal process (p- V) graph is a rectangular hyperbola while it is a straight line. So, to see the behaviour of temperature, First we will find either (T - V) equation or (T _ p) equation and from that equation we can judge how the temperature baries. From the graph, first we will write )p V) equation, then we will convert it either in (T - V) equation or in (T - p) quation with the help of equation, (pV = nRT).
View SolutionVirial equation is: PVM=RT[A+BVM+CVM2+…], where A, B, C, …. are first second,third, … virial coefficent, respectively, For an ideal gas
View SolutionThe van der Waal's equation of state for some gases can be expressed as :
(P+aV2)(V−b)=RT
Where P is the pressure , V is the molar volume , and T is the absolute temperature of the given sample of gas and a,b,andR are constants.
Which of the following does not have the same dimensional formula as that for RT?
View SolutionThe van der Waal's equation of state for some gases can be expressed as :
(P+aV2)(V−b)=RT
Where P is the pressure , V is the molar volume , and T is the absolute temperature of the given sample of gas and a,b,andR are constants.
In the above problem , the dimensional formula for RT is same as that of
View Solution
