One mole of a monoatomic real gas satisfies the equation where is a constant. The relationship of interatomic potential and interatomic distance for gas is given by
The correct Answer is:C
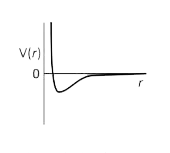
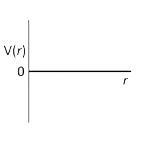
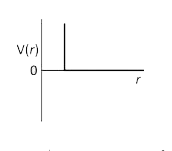
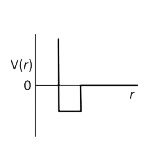
As the given gas equation is .
According to this equation inter particle forces is ignored/neglected.
Hence particles of gas can not get attracted so inter-atomic potential can not be negative.
Now, on further compression particles can’t come closer than a certain distance. So answer must be (C).
Topper's Solved these Questions
- STATES OF MATTERBook:VMC MODULES ENGLISHChapter:STATES OF MATTERExercise:ILLUSTRATION
Explore 30 Videos
- STATES OF MATTERBook:VMC MODULES ENGLISHChapter:STATES OF MATTERExercise:SOLVED EXAMPLES
Explore 20 Videos
- STATES OF MATTERBook:VMC MODULES ENGLISHChapter:STATES OF MATTERExercise:JEE-Main ( ARCHIVE )
Explore 17 Videos
- STATES OF MATTERBook:VMC MODULES ENGLISHChapter:STATES OF MATTERExercise:IMPECCABLE
Explore 50 Videos
- STOICHIOMETRY - IBook:VMC MODULES ENGLISHChapter:STOICHIOMETRY - IExercise:JEE Advanced (Archive)
Explore 31 Videos
Similar Questions
A gas obeys the equation of state P(V−b)=RT (The parameter b is a constnat The slope for an isochore will be .
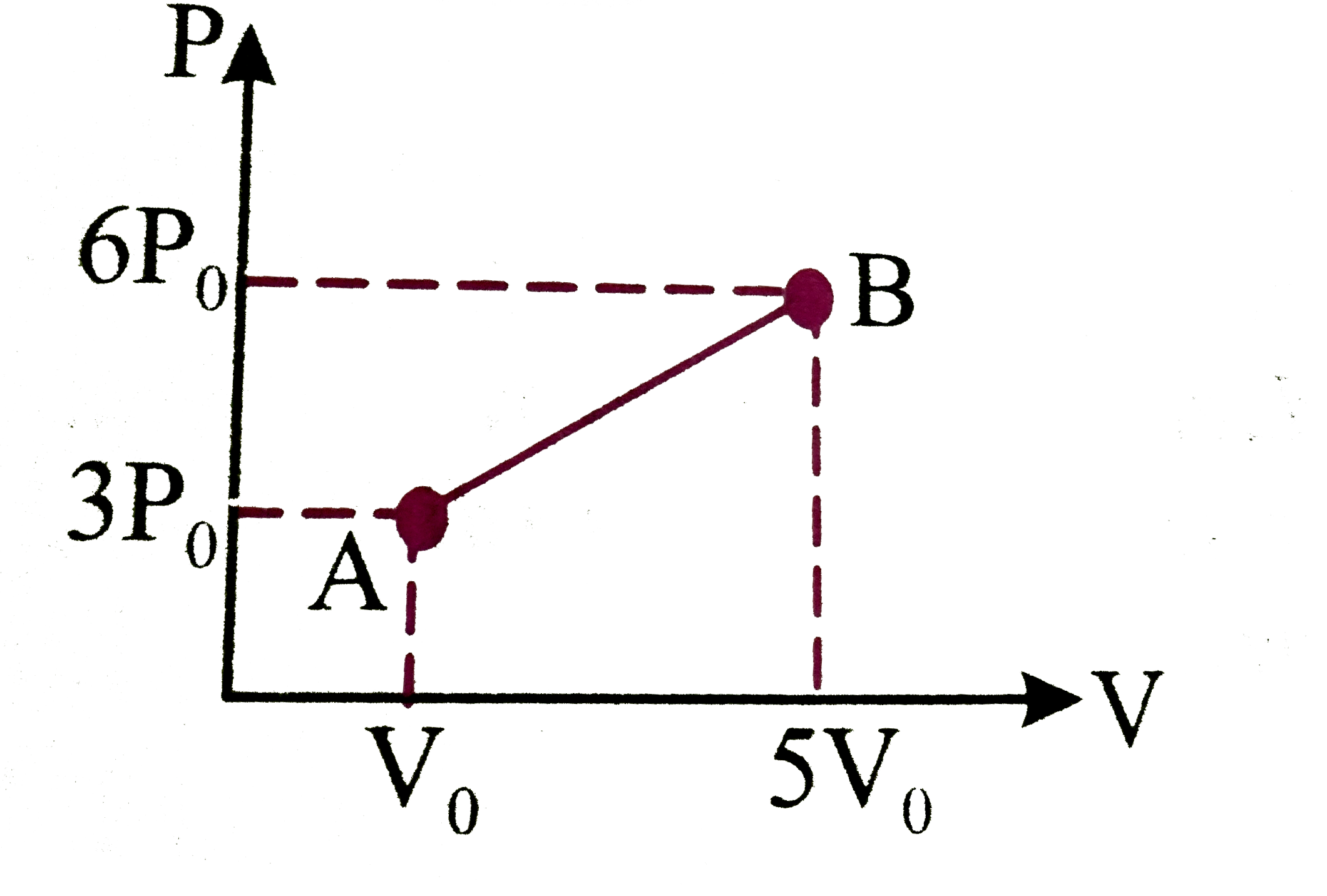
View SolutionOne mole of a monoatomic ideal gas undergoes the process A→B in the given P-V diagram. What is the specific heat for this process?
View SolutionIn a process, temperature and volume of one mole of an ideal monoatomic gas are varied according to the relation VT= K, where K is a constant. In this process the temperataure of the gas is increased by ΔT. The amount of heat absorbed by gas is (R is gas constant).
View SolutionIn a process, temperature and volume of one mole of an ideal monoatomic gas are varied according to the relation VT= K, where K is a constant. In this process the temperataure of the gas is increased by ΔT. The amount of heat absorbed by gas is (R is gas constant).
View SolutionOne mole of an ideal monoatomic gas is taken through a polytropic process P2T = constant. The heat required to increase the temperature of the gas by ΔT is
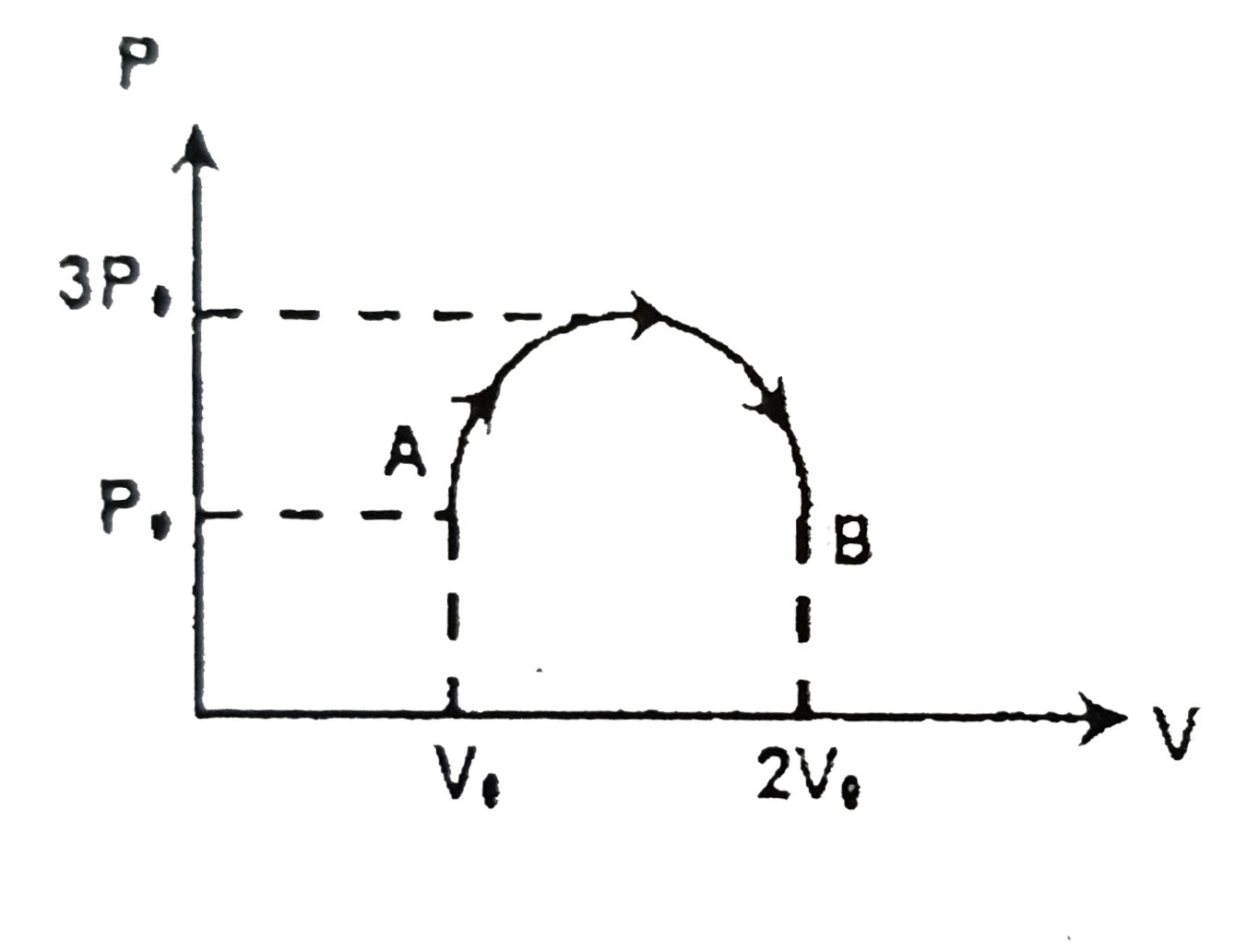
View SolutionOne mole of an ideal monoatomic gas is taken through the thermodynamic process shown in the P−V diagram. The heat supplied to the system is
View SolutionOne mole of an ideal monatomic gas undergoes the process P=αT1/2, where α is constant . If molar heat capacity of the gas is βR1 when R = gas constant then find the value of β.
View SolutionHeart leaks into a vessel, containing one mole of an ideal monoatomic gas at a constant rate of R4s−1 where R is universal gas constatant. It is observed that the gas expands at a constant rate dVdt=V0400(second) where V0 is intial volume. The inital temperature is given by T0=40K. What will be final temperature of gas at time t=400s.
View SolutionOne way of writing the equation of state for real gases is
PV=RT[1+BV+….]
where B is a constant. Derive an approximate expression for B in terms of the van der Waals constants a and b.
View SolutionIn van der Waal's equations (P+aV2)(V−b)=RT, what are the dimensions of the constants a and b?
View Solution