A constant force produces maximum velocity V on the block connected to the spring of force constant K as shown in the figure. When the force constant of spring becomes 4K, the maximum velocity of the block is

The correct Answer is:V/2
By work energy theorem,
wext+wspring=kf−ki
Let x1,x2 be the initial and final extensions and
v,v' initial and final velocities
initially,
Fx1−12kx12=12mv2…..(1)
and finially Fx2−12k′x22=12mv'2.....(2)
In both cases : force applied is same, and velocity become maximum when HF=kx. (at equilibrium)
(after which the mass will deaccelerate)
∴F=kx1=(4k)x2⇒x2=x14,(k'=4k)
Substituting in (2)
fx2−12k'x22=12mv'2
Fx14−12(4K)(x14)2=12mv2⇒14[Fx1=12kx12]=12mv2...(3)
Dividing (3)/(1): we get :
14=v2v2⇒v'=v2
Topper's Solved these Questions
Similar Questions
A block of mass m is suspended by different springs of force constant shown in figure.

View SolutionForce constant of a spring (k) is anonymous to
View SolutionDefine spring constant or force constant.
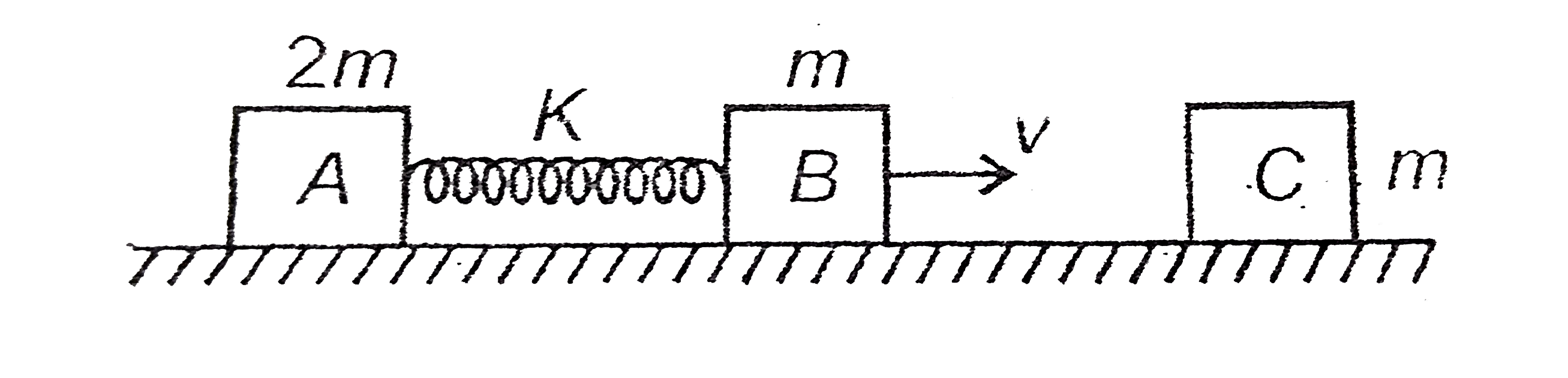
View SolutionTwo blocks A and B of mass 2m and m respectively are connected to a massless spring of force constant K as shown in figure A and B are moving on the horizontal frcitionless surface with velocity v to right with underformed spring. If B collides with C elastically, then maximum compression of the spring will be
View SolutionA block of mass m sliding n a smooth horizontal surface with velocity →v meets a long horizontal spring fixed ast one end and having spring constant k as shown n figure. Find the maximum compression of the spring. Will the velocity of the block be the same as v whenit comes back to the original position shown?

View SolutionA block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.

View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is

View SolutionA block of mass m is connected to a spring of force constant k. Initially the block is at rest and the spring has natural length. A constant force F is applied hrizontally towards right. The maximum speed of the block will be (there is no friction between block and the surface)

View SolutionTwo identical blocks A and B are connected with a spring of constant k as shown in ligure. If block B s moving rightward with speed V0 maximum extension of spring is
View Solution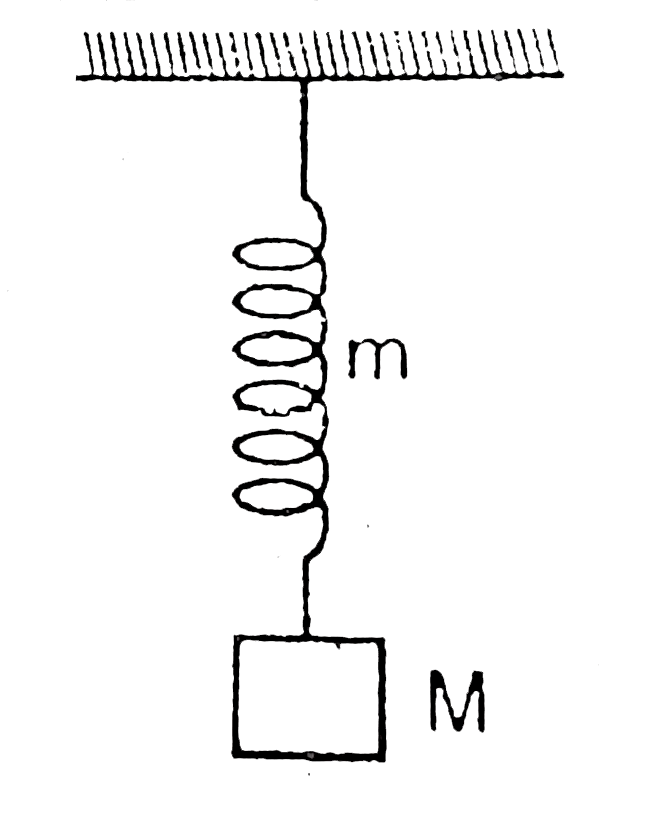
A block of M is suspended from a vertical spring of mass m as shown in the figure. When block is pulled down and released the mass oscillates with maximum velocity v.
View Solution
